4.2.2. Вращение твердого тела вокруг неподвижной оси

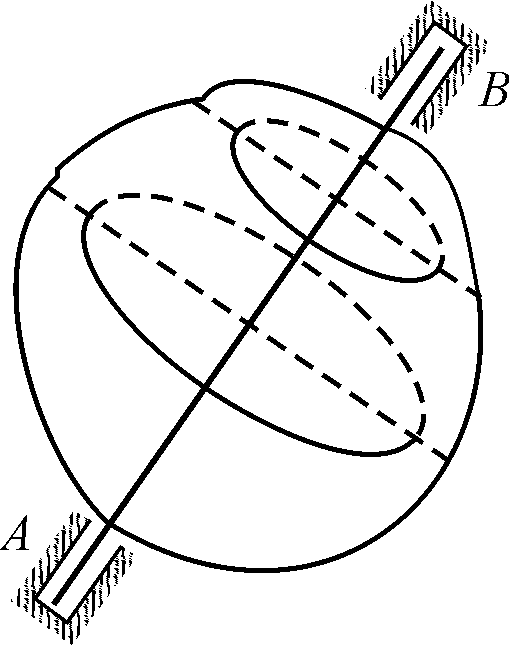
Рассмотрим движение твердого тела с двумя неподвижными точками А и В (рис. 4.4). Из условия неизменяемости расстояния между любыми точками тела вытекает, что все точки на прямой АВ остаются неподвижными. Прямая АВ называется осью вращения, а движение тела называется вращательным. Нетрудно видеть, что все точки тела описывают дуги окружностей с центрами на ось вращения.

Рис. 4.4.

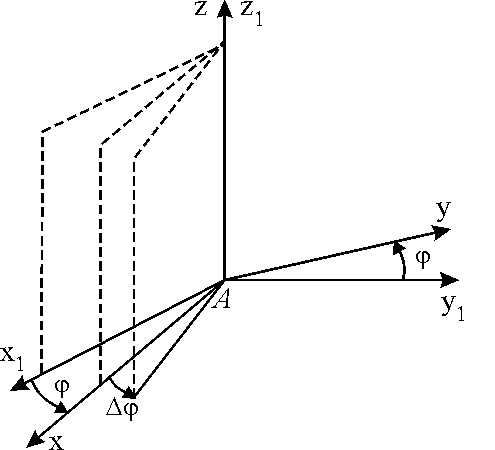
Рис. 4.5.

Направим ось Аz₁ неподвижной системы координат Аx₁y₁z₁ по оси вращения тела. Введем подвижную систему координат Axyz, жестко связанную с телом, ось Az которой так же направим по оси вращения (рис. 4.5). Положение тела будет однозначно определено углом поворота тела

между неподвижной плоскостью x₁Аz₁ и подвижной плоскостью xAz (рис. 4.5). Условимся считать положительным направлением отсчета направление против хода часовой стрелки, если смотреть с конца оси Oz₁.

Пусть в момент времени угол между неподвижной полуплоскостью x₁Аz₁ и подвижной полуплоскостью хАz равен , а в момент времени равен . Это значит, что за промежуток времени подвижная плоскость, а следовательно, и тело повернулись на угол

.

Отношение

называется средней угловой скоростью тела за промежуток времени .

Предел этого отношения при называется угловой скоростью тела в данный момент времени

. (4.5)

Единица измерения угловой скорости в системе СИ есть 1/с.

Вектором угловой скорости твердого тела, совершающего вращение вокруг неподвижной оси, называется вектор, модуль которого равен абсолютному значению производной угла поворота тела по времени, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки

. (4.6)

Из этой формулы следует, что при направление вектора совпадает с направлением вектора k, а при вектор направлен в сторону, противоположную направлению вектора k.

В технике часто при равномерном вращении тела пользуются числом оборотов в минуту. Зависимость между угловой скоростью и числом оборотов в минуту определяется по следующей формуле:

,

где  – число оборотов в минуту.

Предположим, что в момент времени угловая скорость вращения равна , а в момент равна . Величина

называется средним угловым ускорением тела за промежуток времени .

Предел этого отношения при называется угловым ускорением тела в данный момент времени

. (4.7)

Единица измерения углового ускорения – 1/с².

Вектором углового ускорения называется вектор, равный производной по времени от вектора угловой скорости, т.е.

. (4.8)

Из формулы (4.8) следует, что вектор , так же как и вектор , направлен вдоль оси вращения. Величины и представляют проекции векторов угловой скорости и углового ускорения на ось вращения.

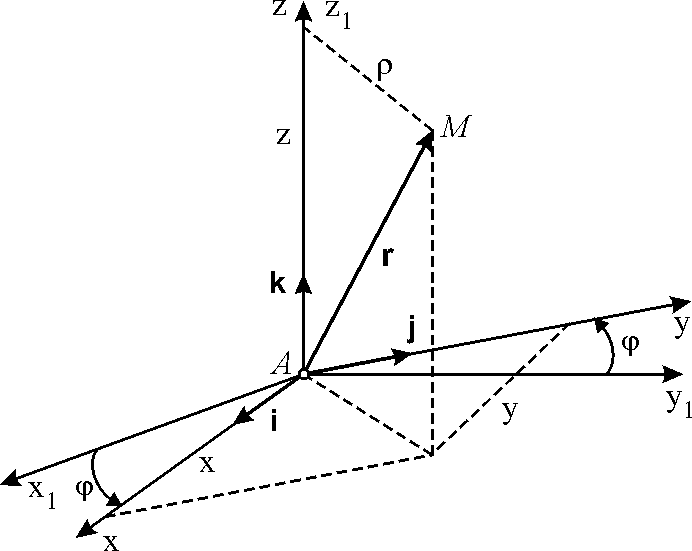
Найдем скорости и ускорения любой точки тела, вращающегося вокруг неподвижной оси (рис. 4.6). Радиус-вектор произвольной точки М в подвижной системе координат Axyz ( , , ) можно представить в виде

. (4.9)

Скорость точки М будет равна

Рис. 4.6.

. (4.10) Поскольку вектор k неподвижен, то k=0. Производные векторов i и j вычислены ранее при рассмотрении движения точки в полярной системе координат. Обозначая и из формул (3.12), (3.13) и (4.5) получим

.

Тогда формула (4.10) запишется в виде

. (4.11)

Так как векторное произведение

имеет те же проекции на оси х, у и z, что и вектор скорости v, то имеем

, (4.12)

иначе говоря, скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус-вектор этой точки.

Из формулы (4.12) следует, что

,

т.е. модуль скорости любой точки твердого тела равен произведению модуля угловой скорости тела на расстояние от точки до оси вращения. Направлен же вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону ее движения.

Дифференцируя по времени равенство (4.12), получим

,

или .

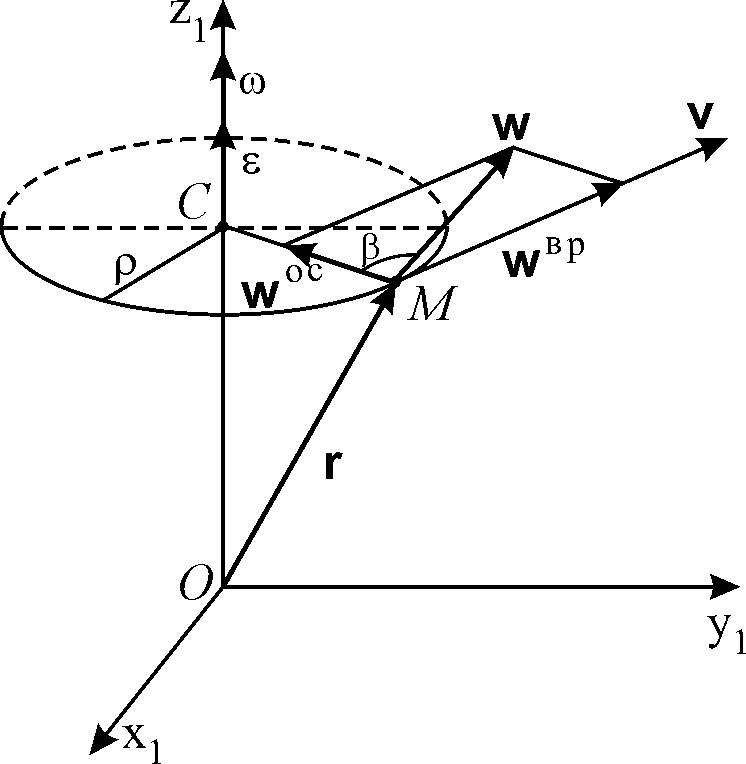
Вектор направленный по касательной к траектории точки, т.е. параллельно скорости (рис. 4.7), называется вращательным ускорением точки М тела, т. е.

.

Численное значение вращательного ускорения равно

.

Рис. 4.7.

Вектор , лежащий в плоскости окружности радиуса и направленный к оси вращения, называется осестремительным ускорением. Так как вектор v перпендикулярен вектору , то численное значение осестремительного ускорения равно .

Модуль полного ускорения точки М будет

.

Угол , образованный векторами полного и осестремительного ускорений, определяется из формулы

.