4.2. Простейшие движения твердого тела

4.2.1. Поступательное движение твердого тела

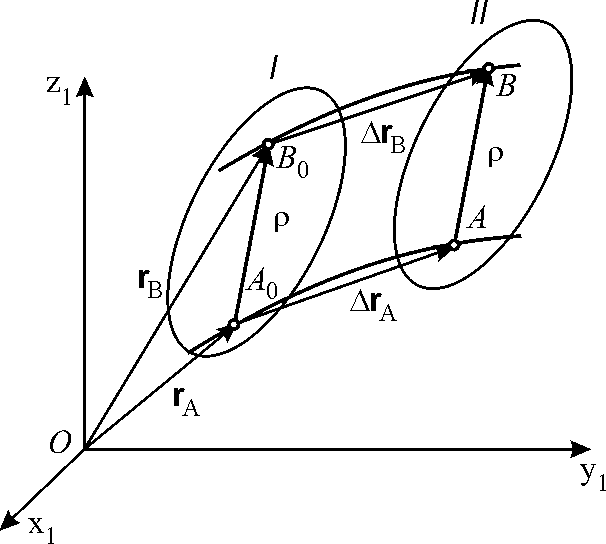
Поступательным движением твердого тела называется такое движение, при котором любая, прямая, проведенная в теле, остается во все время движения параллельной своему первоначальному положению.

Рис. 4.2.

Пусть твердое тело движется поступательно относительно системы координат (рис. 4.2),  – радиус-вектор точки А,  – радиус-вектор точки В, а  – радиус-вектор, определяющий положение точки В в подвижной системе координат Axyz, жестко связанной с телом (на рис. 4.2 эта система не показана).

Так как рассматриваемое тело абсолютно твердое и его движение поступательное, то вектор при движении тела не меняет модуля и направления.

Из рассмотрения рис. 4.2 следует

. (4.3)

Пусть в момент времени тело занимало положение , а в момент времени  – положение (рис. 4.2). Тогда будет вектором перемещения точки А, а  – вектором перемещения точки В за промежуток времени .

Во время движения вектор не изменяется, значит, отрезки А₀В₀ и АВ равны и параллельны и, следовательно, фигура А₀В₀ВА — параллелограмм.

Таким образом,

,

т.е. при поступательном движении абсолютно твердого тела перемещения всех его точек геометрически равны между собой.

Из равенства (4.3) и условия постоянства вектора также следует, что траектории точек тела, движущегося поступательно, одинаковы и получаются друг из друга параллельным смешением.

Продифференцировав выражение (4.3) по времени, получим

,

но так как , то и, следовательно,

или .

Дифференцируя полученное соотношение по времени, получим

или ,

т.е. при поступательном движении твердого тела скорости и ускорения всех его точек в каждый момент времени равны между собой.

Таким образом, при поступательном движении твердого тела все его точки движутся одинаково, так как их перемещения, скорости и ускорения геометрически равны. Следовательно, поступательное движение твердого тела определяется движением одной точки этого тела, координаты которой должны быть заданы как функции времени, т.е.

, , .

Пользуясь понятием поступательного движения, докажем теорему о сложении скоростей точки, совершающей сложное движение.

Предположим, что точка М движется по отношению к системе координат Axyz, которая жестко связана с телом, перемещающимся поступательно по отношению к неподвижной системе координат Ox₁y₁z₁.

Рис. 4.3.

Положение точки относительно неподвижной системы координат определяется радиусом-вектором (рис. 4.3) , где  – радиус-вектор начала подвижной системы координат,  – радиус-вектор, определяющий положение точки М в подвижной системе координат.

Дифференцируя это равенство по времени, получим

.

В этом равенстве есть скорость точки относительно неподвижной системы координат, которая называется скоростью точки в сложном движении или абсолютной скоростью и обозначается через .

Первое слагаемое в правой части равенства  – скорость точки А. Так как система координат Ахуz движется поступательно, то это одновременно будет скоростью той точки тела, с которой в данный момент совпадает движущаяся точка М. Эта скорость называется переносной скоростью точки М и обозначается .

Вектор определен в подвижной системе координат, следовательно,

.

Так как подвижная система координат перемещается поступательно, то  – постоянные векторы и их производные по времени равны нулю, поэтому .

Это равенство определяет скорость точки по отношению к подвижной системе координат и называется относительной скоростью точки М. Обозначим эту скорость через .

Таким образом, имеем

. (4.4)

Полученное равенство выражает теорему о сложении скоростей: скорость точки в сложном движении равна сумме переносной и относительной скоростей.