8.4. Пара вращений

Рис. 8.5.

Рассмотрим сложное движение, состоящее из двух вращений относительно параллельных осей О1z1 и О2z2 (рис. 8.5). Пусть угловые скорости относительного ( ) и переносного ( ) движений равны по модулю, но противоположно направлены ( ). Такая совокупность движений называется парой вращений.

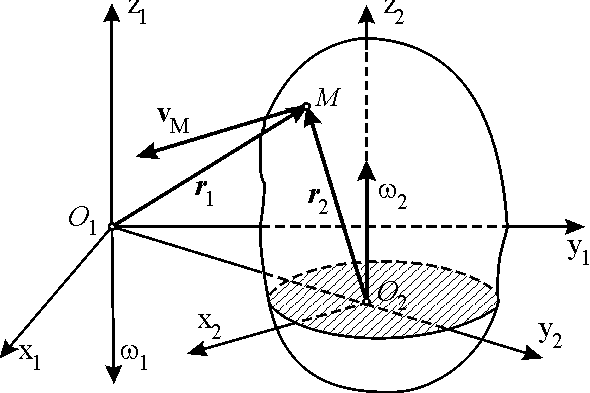
Найдем абсолютную скорость какой-либо точки М твердого тела:

.

В нашем случае

, ,

следовательно,

(8.9)

Векторы и не зависят от положения точки М, поэтому из (8.9) вытекает, что скорости всех точек тела одинаковы. Этим свойством обладает только поступательное движение.

Из (8.9) следует, что

(8.10)

Векторное произведение называется моментом пары вращений. Таким образом, тело, участвующее в паре вращений, движется поступательно со скоростью, равной моменту пары вращений. Легко видеть, что совокупность пар вращений эквивалентна одной паре, т.е. поступательному движению. Заметим, что любое мгновенно-поступательное движение можно представить как мгновенную пару вращений.

8.5. Сложение вращений вокруг параллельных осей

Из содержания предыдущих параграфов видно, что введенные выше простейшие кинематические элементы – угловые скорости вращения тела (или системы координат) и скорости поступательных движений подчиняются тем же законам, что и силы и пары в статике. В самом деле, пары вращений или поступательные движения аналогичны парам сил. Как и в статике, совокупность кинематических пар эквивалентна паре, момент которой (или скорость результирующего поступательного движения) равен сумме моментов слагаемых пар.

Угловые скорости вращения вокруг осей, пересекающихся в одной точке, заменяются одной угловой скоростью так же, как и сходящаяся система сил в статике приводится к одной силе (равнодействующей). Аналогия между угловыми скоростями составляющих вращений и силами этим не ограничивается. Мы сейчас установим, что сложение вращений вокруг параллельных осей совершенно аналогично сложению параллельных сил.

Рис. 8.6.

Предположим, что тело вращается с угловой скоростью вокруг оси О₂z₂ относительно системы координат О₂x₂y₂z₂, а последняя вращается с угловой скоростью вокруг оси О₁z₁ относительно системы координат О₁x₁y₁z₁, причем оси О₁z₁ и О₂z₂ параллельны (рис. 8.6).

Тогда абсолютная скорость любой точки М тела

.

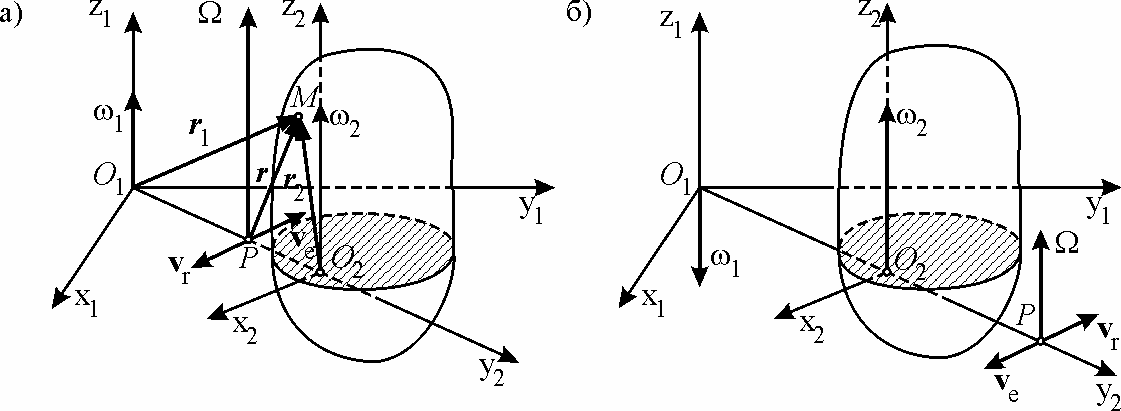
Скорости и точки М расположены в плоскости, перпендикулярной осям О₁z₁ и О₂z₂, следовательно, и абсолютная скорость точки М лежит в плоскости, перпендикулярной этим осям. Так как точка М произвольна, то это означает, что тело участвует в плоском движении. Найдем в плоскости x₁О₁y₁ мгновенный центр скоростей в случае, когда и направлены в одну сторону (рис. 8.6 а).

Для точки Р, лежащей на прямой O₁O₂, и коллинеарные, но направлены в разные стороны. Для того чтобы их геометрическая сумма была равна нулю, должно выполняться равенство

или

. (8.11)

Точка Р делит отрезок O₁O₂ внутренним образом на части, обратно пропорциональные модулям угловых скоростей составляющих вращений.

Перейдем теперь к сложению вращений, имеющих противоположные направления. Пусть . Скорости и в этом случае имеют противоположные направления в точках на прямой O₁O₂, расположенных вне отрезка O₁O₂ (рис. 8.6 б). Найдем точку Р, в которой эти скорости равны:

или

. (8.12)

Точка Р делит отрезок O₁O₂ внешним образом на части, обратно пропорциональные модулям угловых скоростей. Такую точку всегда можно найти, если только .

В каждом из рассмотренных случаев точка Р имеет скорость, равную нулю, т. е.

. (8.13)

Найдем теперь скорость произвольной точки М:

.

Здесь  – радиус-вектор точки М относительно мгновенного центра скоростей Р. Раскрывая скобки в правой части и используя равенство (8.13), получим

, (8.14)

где .

Отсюда следует, что совокупность двух вращений, происходящих вокруг параллельных осей, но не представляющих собой пары вращений, приводится к одному вращению, мгновенная ось которого делит внутренним или внешним образом расстояние между осями составляющих вращений на части, обратно пропорциональные модулям угловых скоростей. Угловая скорость результирующего вращения равна геометрической сумме угловых скоростей составляющих движений.

Если угловые скорости направлены в одну сторону, то мгновенная ось вращения расположена между осями О₁z₁ и О₂z₂ и модуль результирующей угловой скорости . В случае противоположно направленных вращений мгновенная ось расположена за осью, вокруг которой вращение происходит с большей угловой скоростью и . Результирующая угловая скорость направлена в сторону большей из угловых скоростей.