8.2. Сложение поступательных движений

Рис. 8.1.

Пусть  – скорость поступательного движения тела Р относительно системы О2x2y2z2 (рис. 8.1), a  – скорость поступательного движения системы О2x2y2z2 относительно неподвижной системы координат О1x1y1z1. Тогда, чтобы найти абсолютную скорость какой-либо точки М тела Р, нужно применить теорему о сложении скоростей:

. (8.1)

В нашем случае и следовательно,

. (8.2)

Таким образом, у всех точек тела абсолютные скорости оказались одинаковыми, следовательно, при сложении поступательных движений твердого тела результирующее движение будет также поступательным и скорость результирующего движения равна сумме скоростей составляющих движений.

В случае поступательных движений, применяя последовательно формулу (8.1), можно показать, что результирующее движение также будет поступательным и его скорость будет равна сумме скоростей составляющих движений, т.е.

.

Возможен случай, когда скорости всех точек тела только в данный момент времени оказываются равными между собой. Этот случай называют мгновенно-поступательным движением. Однако следует иметь в виду, что ускорения точек при этом различны.

8.3. Сложение вращений вокруг пересекающихся осей. Кинематические уравнения Эйлера

Рис. 8.2.

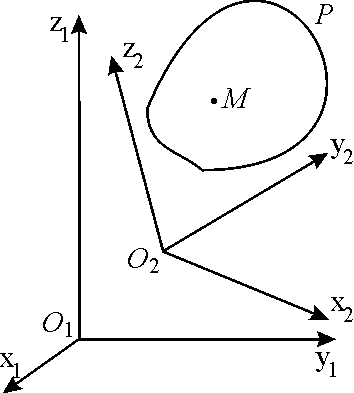
Пусть тело Р вращается в системе координат Оx2y2z2 вокруг оси z2 с угловой скоростью , а система координат Оx2y2z2 вращается вокруг оси z1 неподвижной системы с угловой скоростью (рис. 8.2). Точка О остается неподвижной, поэтому результирующее движение тела будет сферическим. Обозначим через угловую скорость этого движения. Наша задача состоит в том, чтобы

найти угловую скорость абсолютного движения тела, зная угловые скорости и составляющих вращений.

Найдем абсолютную скорость произвольной точки М тела. Для этого в формулу (8.1) следует подставить

, ,

где  – радиус-вектор точки М; тогда

.

С другой стороны, скорость той же точки М в абсолютном движении будет равна

.

Сравнивая оба равенства, получим

.

Так как точка М, а следовательно, и ее радиус-вектор произвольны, то

. (8.3)

Из формулы (8.3) следует, что совокупность двух вращений, происходящих вокруг пересекающихся осей, эквивалентна одному вращению, происходящему с мгновенной угловой скоростью, равной сумме угловых скоростей составляющих вращений.

Замечание. В случае из (8.3) следует, что . Следовательно, совокупность двух вращений вокруг одной и той же оси, происходящих с одинаковыми по модулю, но противоположно направленными угловыми скоростями, эквивалентна покою. Такую совокупность движений всегда можно присоединять к любому сложному движению тела.

Совокупность вращений вокруг пересекающихся в одной точке осей эквивалентна одному вращению с мгновенной угловой скоростью

.

Полученное правило сложения вращений вокруг пересекающихся осей позволит нам теперь выразить проекции мгновенной угловой скорости тела, имеющего одну неподвижную точку О, через углы Эйлера и их производные.

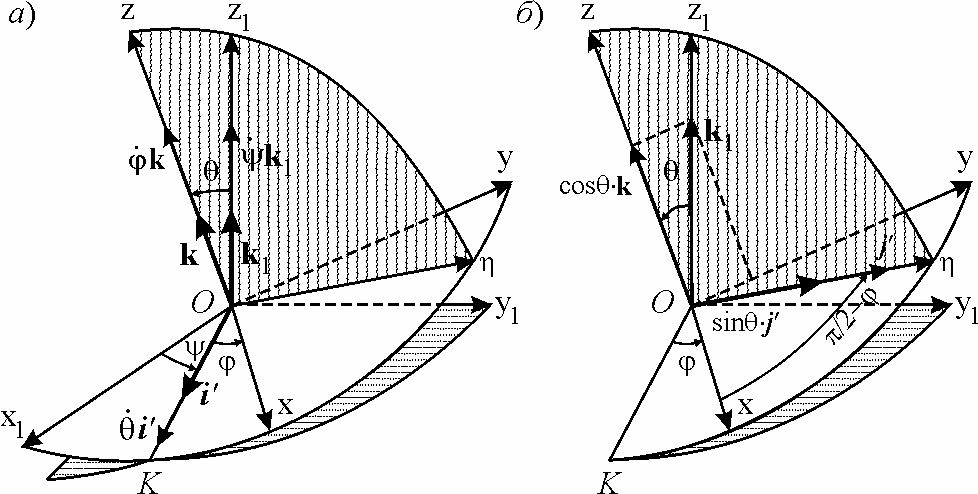
Рис. 8.3.

Напомним, что положение подвижной системы координат Oxyz, жестко связанной с телом, полностью определяется относительно неподвижной системы координат Оx₁y₁z₁ углами Эйлера (рис. 8.3). Тело участвует в трех вращениях: первое вращение, соответствующее изменению угла прецессии , происходит вокруг неподвижной оси Оz₁ с угловой скоростью ; второе вращение, соответствующее изменению угла нутации , происходит вокруг линии узлов ОК с угловой скоростью , где  – единичный вектор линии узлов; наконец, третье вращение, соответствующее изменению угла собственного вращения , происходит вокруг оси Oz с угловой скоростью . Следовательно, абсолютная угловая скорость тела будет

, (8.4)

Составим таблицу направляющих косинусов единичных векторов в системе подвижных осей Oxyz:

			0
	0	0	1

Поясним составление первой строки этой таблицы (вторая и третья строки непосредственно следуют из рис. 8.3 а). Разложим единичный вектор на две взаимно перпендикулярные составляющие, направив одну из них по оси z (она равна , см. рис. 8.3 б); тогда вторая составляющая, равная , где  – единичный вектор вспомогательной оси , будет находиться в плоскости ху. Следовательно,

. (8.5)

Вспомогательная ось составляет с осями х и у углы и . Проектируя единичный вектор на оси х, у и z, получим (напомним, что проекции единичных векторов равны соответствующим направляющим косинусам)

, , .

Эти выражения и составляют первую строку таблицы направляющих косинусов.

Проектируя теперь обе части равенства (8.4) на оси х, у и z и учитывая таблицу косинусов, найдем проекции вектора угловой скорости тела на оси, жестко связанные с телом:

(8.6)

Полученные соотношения носят название кинематических уравнений Эйлера.

Модуль угловой скорости определяется равенством

. (8.7)

Таблица направляющих косинусов между единичными векторами в системе неподвижных осей Оx₁y₁z₁ имеет вид

	0	0	1
			0

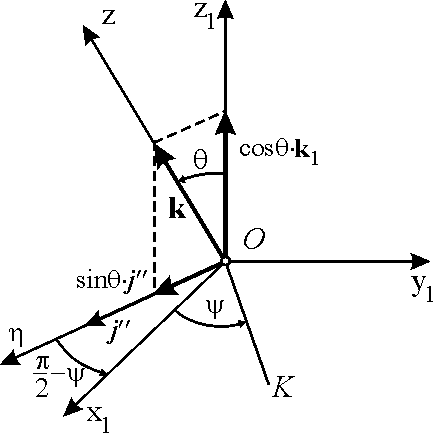
Для того чтобы получить последнюю строку, мы разложили вектор на две составляющие, направив одну из них по оси (она равна ; см. рис. 8.4); тогда вторая, равная , где  – единичный вектор новой вспомогательной оси , будет находиться в плоскости Оx₁y₁:

Рис. 8.4.

. Третья строка второй таблицы получена проектированием этого равенства на оси , , и пользуясь второй таблицей направляющих косинусов, найдем проекции вектора угловой скорости на неподвижные оси координат:

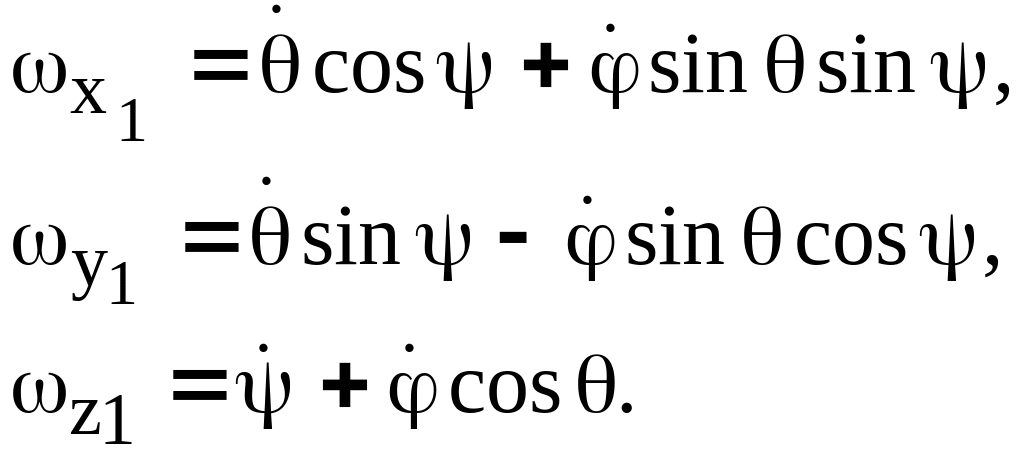(8.8)

Кинематические уравнения Эйлера (8.6) и (8.8) устанавливают связь между проекциями вектора угловой скорости на соответствующие оси, углами Эйлера и их первыми производными по времени.