6.3. Ускорения точек тела, имеющего одну неподвижную точку

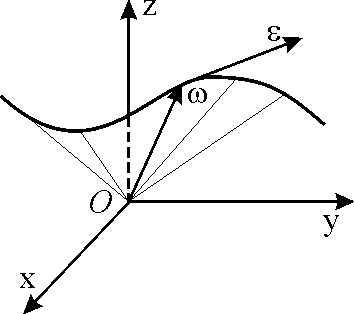
Введем прежде всего понятие углового ускорения. Угловым ускорением называется производная угловой скорости по времени, т.е.

. (6.15)

Рис. 6.4.

Из определения видно, что вектор углового ускорения можно рассматривать как скорость конца вектора (рис. 6.4). Угловое ускорение направлено по касательной к годографу вектора угловой скорости (рис. 6.4), поэтому его направление может быть каким угодно в зависимости от закона изменения

вектора угловой скорости. Заметим попутно, что годограф вектора угловой скорости – кривая, лежащая на неподвижном аксоиде (рис. 6.4).

Перейдем теперь к определению ускорения произвольной точки тела. Исходя из определения ускорения и используя равенство (6.10), получим

.

Но , а ,

следовательно,

. (6.16)

Таким образом, ускорение может быть представлено как сумма двух ускорений: и .

Ускорение называется вращательной составляющей ускорения. Модуль этого ускорения равен

,

где  – расстояние от точки М до вектора . Направлено это ускорение перпендикулярно плоскости векторов и в ту сторону, откуда кратчайший переход от вектора к вектору виден против хода часовой стрелки. Заметим, что вследствие несовпадения направлений угловой скорости и углового ускорения вращательная составляющая ускорения может быть направлена по отношению к направлению скорости под любым углом, оставаясь перпендикулярной вектору . В этом существенное различие между вращением твердого тела вокруг неподвижной оси и движением тела, имеющего одну неподвижную точку.

Рис. 6.5.

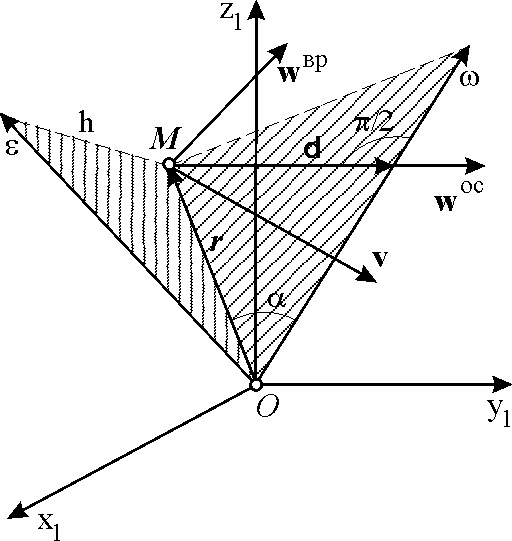
Ускорение направлено по перпендикуляру к плоскости векторов и , т.е. по направлению вектора d (рис. 6.5), имеющего начало в точке М и конец в основании перпендикуляра, опущенного из точки М на мгновенную ось вращения. Модуль векторного произведения равен , т.к. .

Следовательно, можно записать

. (6.17)

Это ускорение называется осестремительной составляющей ускорения.

Итак, ускорение любой точки тела равно сумме вращательной и осестремительной составляющих ускорения

. (6.18)

6.4. Движение свободного твердого тела

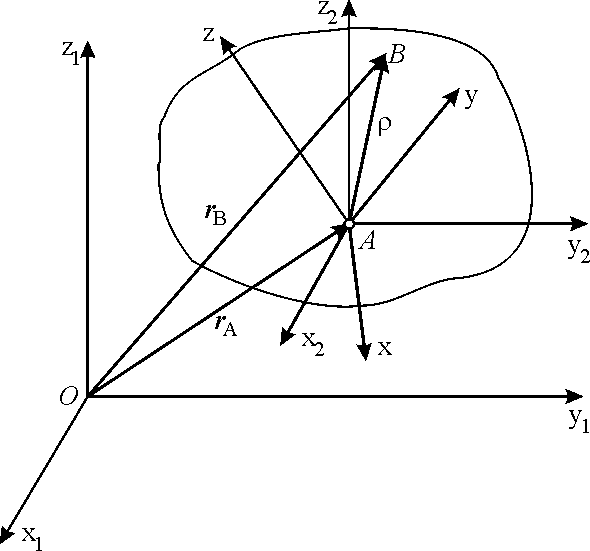
Рассмотрим движение свободного твердого тела. Введем, кроме неподвижной системы координат Ох₁y₁z₁ еще подвижную систему координат Aх₂y₂z₂, перемещающуюся поступательно относительно осей Ох₁y₁z₁ и связанную с телом только в одной точке – точке А, и подвижную систему координат Axyz, жестко связанную с телом (рис. 6.6). В подвижной системе

Рис. 6.6.

координат Aх2y2z2 тело имеет одну закрепленную в ней точку – точку А, следовательно, тело в этой системе координат участвует в движении, рассмотренном нами в предыдущем параграфе. Для того чтобы задать положение тела в подвижной системе координат Aх2y2z2, можно ввести три угла Эйлера , а для определения

положения относительно неподвижной системы координат нужно, кроме того, задать положение точки А, для чего потребуется знать еще три величины: x_lA, y_lA, z_lA. Таким образом, положение свободного твердого тела определяется шестью независимыми параметрами: x_lA, y_lA, z_lA, .

Перейдем к определению скоростей точек свободного тела. Скорость произвольной точки В равна производной от ее радиуса-вектора по времени. Пользуясь рис. 6.6, найдем

.

Следовательно,

. (6.19)

Заметим, что  – скорость точки А; кроме того, вектор представляет собой скорость точки В относительно подвижной системы координат Aх₂y₂z₂, в которой тело имеет одну закрепленную точку. Следовательно, согласно формуле (6.10) .

Таким образом, формулу (6.19) можно переписать в виде

. (6.20)

Здесь  – угловая скорость вращения тела относительно системы координат Aх₂y₂z₂. (Так же как и для плоского движения, можно показать, что угловая скорость не зависит от выбора полюса).

Формулу (6.20) можно прочитать следующим образом: скорость любой точки свободного твердого тела геометрически складывается из скорости произвольно выбранного полюса и скорости этой точки во вращательном движении тела относительно полюса.

Пользуясь формулой (6.20), можно доказать следующую теорему:

Проекции скоростей двух точек свободного твердого тела на прямую, проходящую через эти точки, равны, между собой.

Согласно равенству (6.20) имеем

,

но вектор перпендикулярен вектору ; следовательно, и . Определим ускорения точек свободного твердого тела. Для этого продифференцируем по времени равенство (6.20):

. (6.21)

Замечая, что ,  – угловое ускорение тела в подвижной системе координат Aх₂y₂z₂, а , получим

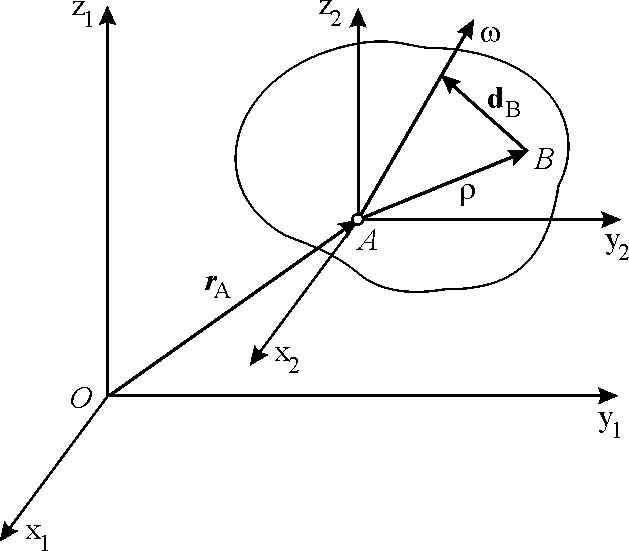
Используя (6. 17), можно записать

.

где  – вектор, имеющий начало в точке В, а конец в основании перпендикуляра, опущенного из В на (рис. 6.7).

Рис. 6.7.

В окончательном виде ускорение точки свободного тела выражается следующим образом: . (6.22) Два последних члена дают ускорение точки В в ее движении вокруг полюса. Таким образом, ускорение точки свободного тела равно

геометрической сумме ускорения полюса и ускорения этой точки в ее движении вокруг полюса.