77

1. Основные понятия и определения

Кинематика – это раздел теоретической механики, в котором изучают механическое движение материальных тел без рассмотрения условий, вызывающих или изменяющих это движение.

Движение материальных тел происходит в пространстве и во времени. Пространство рассматривается как трехмерное евклидово, время в этом пространстве одинаково во всех его точках и не зависит от движения материальных тел.

Под механическим движением понимают изменение положения одного тела относительно другого.

Системой отсчета называют систему координат, связанную с одним из тел. Если тело движется, то система отсчета подвижна, если тело в покое, то система отсчета неподвижна.

Материальной точкой считают твердое тело, размерами которого в данной задаче можно пренебречь.

Абсолютно твердым телом или просто твердым телом называют любую совокупность материальных точек, расстояние между которыми не меняется при любых взаимодействиях.

Основные задачи кинематики:

1. Установление закона движения тела по отношению к выбранной системе отсчета.

2. Определение по заданному закону движения тела кинематических характеристик этого движения (траектория, скорость, ускорение и т.д.).

Непрерывную кривую, которую описывает точка при своем движении, называют траекторией точки. В задачах небесной механики траекторию именуют также орбитой. Если траектория точки является прямой линией, то движение точки называют прямолинейным. Если же траектория – кривая линия (не обязательно плоская), то движение точки называется криволинейным.

2. Краткие сведения из векторного анализа

2.1. Вектор называется вектор-функцией скалярного аргумента , если каждому значению скаляра из области допустимых значений соответствует определенное значение вектора . Будем это записывать так:

.

Если вектор является вектор-функцией скалярного аргумента , то координаты вектора также будут функциями аргумента :

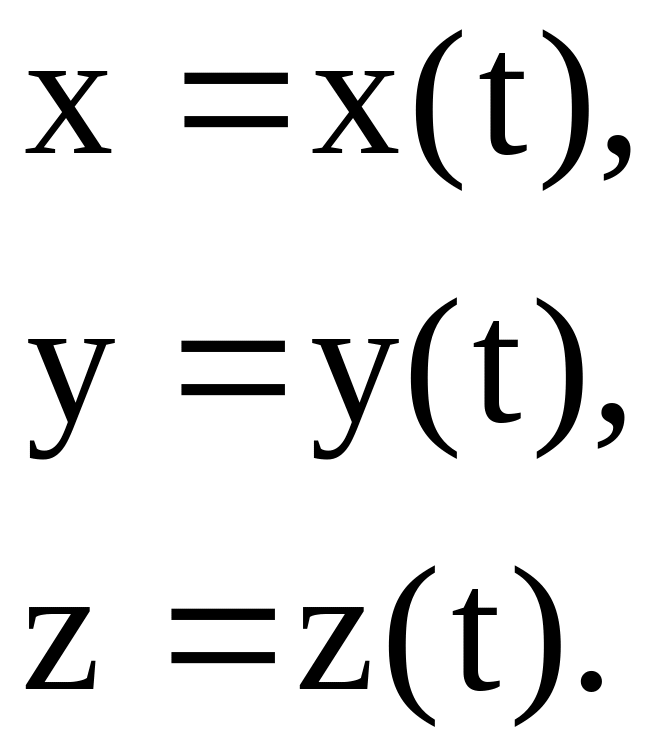
Обратно, если координаты вектора являются функциями , то функцией будет и сам вектор :

.

Таким образом, задание вектор-функции равносильно заданию трех скалярных функций .

2.2. Годографом вектор-функции скалярного аргумента называется геометрическое место точек, которое описывает конец вектора при изменении скаляра , когда начало вектора помещено в фиксированную точку О пространства (рис. 2.1).

Рис. 2.1.

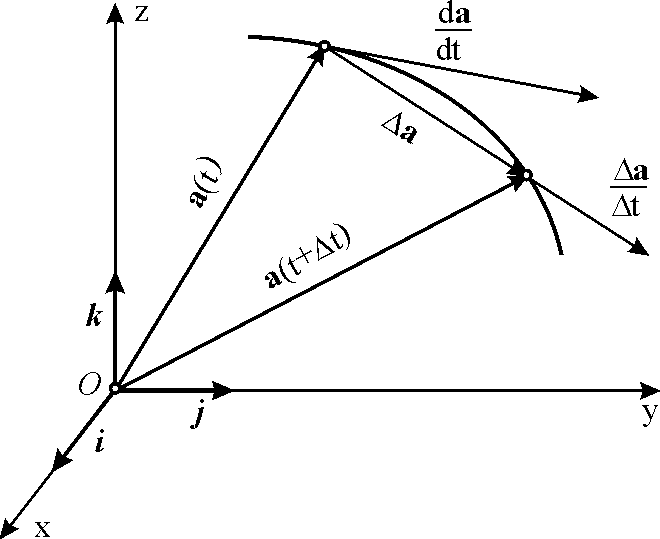
2.3. Производная вектор-функции скалярного аргумента. Пусть вектор задан в какой-либо системе координат как непрерывная функция скалярного аргумента

.

При изменении аргумента будут меняться как модуль вектора , так и его направление. Конец вектора при изменении аргумента описывает кривую – годограф вектора (рис. 1.6). Пусть  – некоторое фиксированное значение аргумента, а  – его приращение. Тогда при значении аргумента вектор будет иметь другой модуль и другое направление, чем при значении аргумента, равном .

Разность

называется приращением вектора .

Предел отношения

при , если он существует, называется производной вектора по скалярному аргументу и обозначается через , т.е.

.

Заметим, что вектор всегда направлен по секущей годографа вектора (рис. 1.6), а значит, и вектор направлен также по секущей. При секущая займет предельное положение, совпадающее с касательной к годографу вектора . Следовательно, производная

Рис. 2.2.

вектора по скалярному аргументу всегда направлена по касательной к годографу этого вектора.