
Rybleva_teoria veroatnosti_2014
.pdf6.10Обувной магазин продал 200 пар обуви. Вероятность того, что в магазин будет возвращена бракованная пара равна 0,01. Найти вероятность того, что из проданных пар обуви будет возвращено:
а) ровно 4 пары; б) ровно 5 пар.
6.11Игра состоит в набрасывании колец на колышек. Игрок получает 6 колец и бросает кольца до первого попадания. Найти вероятность того, что хотя бы одно кольцо останется неизрасходованным, если вероятность попадания при каждом броске равна 0,1.
6.12Изделия некоторого производства содержат 0,1% брака. Какова вероятность, что из 5000 изделий:
а) хотя бы одно бракованное; б) не менее 3 бракованных?
6.13Завод отправил на базу 10000 стандартных изделий. Среднее число изделий, повреждаемых при транспортировке, составляет 0,02%. Найти вероятность того, что из этой партии изделий:
1) будет повреждено: а) 3; б) по крайней мере 3; 2) не будет повреждено: а) 9997; б) хотя бы 9997.
6.14На экономическом факультете на первом курсе учится 1825 студентов. Найти вероятность того, что 15 октября является днем рождения одновременно четырѐх студентов.
6.15Для данного баскетболиста вероятность забросить мяч в корзину при броске равна 0,4. Произведено 10 бросков. Найти наивероятнейшее число попаданий и соответствующую вероятность.
6.16Стрелок сделал 80 выстрелов; вероятность попадания при каждом
выстреле равна 0,7. Найти вероятность того что: а) стрелок попадает 56 раз; б) число попаданий будет заключено между
50 и 60.
6.17 Контрольную работу по теории вероятностей успешно выполняют в среднем 70% студентов. Какова вероятность того, что из 200 студентов работу успешно выполнят:
а) 150 студентов; б) не менее 100 студентов; в) не более 150 студентов?
71
6.18Какое число n раз нужно подбросить симметричную монету, чтобы вероятность хотя бы одного появления герба была больше 1 α =0,99?
6.19При каждом выстреле с вероятностью α 0,7 поражается цель, а с вероятностью 1 α 0,3 – нет. Какое число n выстрелов нужно произвести для того, чтобы вероятность хотя бы одного поражения цели была больше 0,99?
6.20Какое число n раз нужно наугад выбрать одно из 10000 изделий (каждый раз возвращая его на место), чтобы вероятность хотя бы один раз выбрать некачественное изделие была больше 0,999?
6.21В задаче на схему Бернулли найти значение p , при котором
вероятность P3 2 достигает максимума, и вычислить этот максимум.
Ответы:
6.1 |
P X 0 1/ 8 ; P X 1 3 / 8 ; P X 2 3 / 8 ; |
P X 3 1/ 8 . |
|
|||||||||||||||||||
|
|
5 3 |
; P3 1 |
|
75 |
|
; P3 2 |
15 |
|
; P3 3 |
1 |
|
|
|
||||||||
6.2 |
P3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
. 6.3 0,288. |
|
|||||||
|
|
63 |
|
63 |
|
63 |
|
|
||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6.4 |
1) 0,066; |
|
2) |
а) ≈0,436; |
|
б) 0,738; в) 0,564; г) 1 и 2. 6.5 0,038. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C2nn k |
|
|
|
|
|
||||
6.6 |
0,665; 0,6187; 0,40265. |
6.7 |
|
|
|
|
. 6.8 0,31. 6.9 298. |
|
||||||||||||||
22n k |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6.10 |
а) 0,09; |
б) 0,036. |
6.11 |
0,41. 6.12 а) 0,993; б) 0,875. |
|
|||||||||||||||||
6.13 |
1) |
а) 0,1804; б) 0,3233; |
2) а) 0,1804; б) 0,8572. 6.14 ≈0,1755. |
|
||||||||||||||||||
6.15 4; |
0,251. |
|
6.16 а) ≈0,097; б) ≈0,76. |
6.17 а) ≈0,019; б) ≈1; в) ≈0,938. |
||||||||||||||||||
6.18 |
>6. 6.19 |
> 3. 6.20 |
|
7500. 6.21 |
p =2/3, maxP3 2 =4/9. |
|
||||||||||||||||
|
|
|
|
|
|
1.7. Производящая функция |
|
|
||||||||||||||
|
Пусть производится |
n независимых испытаний, причѐм в первом |
||||||||||||||||||||
испытании вероятность появления события A равна p1, во втором - |
p2 , |
|||||||||||||||||||||
… , |
в |
n -ом |
|
испытании - |
|
|
|
pn ; вероятности непоявления события |
A |
|||||||||||||
72
соответственно равны q1, q2 , … , qn . Обозначим Pn k - вероятность появления события A в n независимых испытаниях ровно k раз.
Производящей функцией вероятностей Pn k называют
функцию, определяемую равенством:
φn z p1z q1 p2z q2 ... pnz qn .
Вероятность Pn k того, что в n независимых испытаниях, в
первом из которых вероятность появления события A равна p1, во втором - p2 и т.д., событие A появится ровно k раз, равна
коэффициенту при zk в разложении производящей функции по степеням z . Например, если n 2 , то
φ2 z p1z q1 p2z q2 p1p2z2 p1q2 p2q1 z q1q2 .
Здесь коэффициент p1p2 при z2 равен вероятности P2 2 того, что событие A появится ровно два раза в двух испытаниях; коэффициент при z1 равен вероятности P2 1 того, что событие A
появится ровно один раз в двух испытаниях; коэффициент при z0 , т.е. свободный член q1q2 равен вероятности P2 0 того, что событие A не появится ни одного раза.
Производящую функцию можно применять и для определения вероятностей Pn k в схеме Бернулли. Кроме того, производящая функция используется и для определения вероятностей в случае когда в различных испытаниях появляются различные события: в первом испытании событие A1, во втором – событие A2 и т.д. Изменяется лишь толкование коэффициентов при различных степенях z . Например, в приведѐнном выше разложении коэффициент определяет
вероятность появления двух событий A1 и A2 .
Пример 7.1 Рабочий обслуживает три станка. Вероятность того, что в
течение часа |
станок не потребует внимания рабочего, для первого |
станка равна |
0,9, для второго – 0,8 и для третьего – 0,7. Найти |
|
73 |
вероятность того, что в течение часа не потребуют внимания рабочего: а) все три станка; б) два станка; в) один станок; г) ни один из станков. Решение: Известные вероятности обозначим: p1 0,9 , p2 0,8 и p3 0,7 . Тогда вероятности того, что в течение часа станок потребует внимания рабочего соответственно равны: q1 0,1, q2 0,2 и q3 0,3 .
Составим производящую функцию:
φ3 z 0,9z 0,1 0,8z 0,2 0,7z 0,3 0.504z3 0.398z2 0.092z 0.006
а) P3 3 0,504 ; б) P3 2 0,398 ; в) P3 1 0,092 ; г) P3 0 0,006 .
■
Задачи для самостоятельного решения:
7.1Из двух орудий произведѐн залп по цели. Вероятность попадания в цель для первого орудия равна 0,8, для второго – 0,9. Найти вероятности следующих событий: а) два попадания в цель; б) одно попадание; в) ни одного попадания; г) не менее одного попадания.
7.2Четыре элемента вычислительного устройства работают независимо. Вероятность отказа первого элемента за время t равна 0,2, второго – 0,25, третьего – 0,3 и четвѐртого – 0,4. Найти вероятность того, что за время t откажут: а) 4 элемента; б) 3 элемента; в) ни один элемент; г) не более двух элементов.
7.3Две батареи по 3 орудия каждая производят залп по цели. Цель будет поражена, если каждая из батарей даст не менее двух попаданий. Вероятности попадания в цель орудиями первой батареи равны 0,4; 0,5; 0,6, второй – 0,5; 0,6 и 0,7. Найти вероятность поражения цели при одном залпе из двух батарей.
Ответы: |
|
|
7.1 а) |
0,72; б) |
0,26; в) 0,02; г) 0,26+0,72=0,98. 7.2 а) 0,006; б) |
0,065; |
в) 0,252; |
г) 0,252+0,423+0,254=0,929. 7.3 0,325. |
74
Глава 2. Случайные величины 2.1. Дискретные случайные величины: способы задания,
числовые характеристики и их свойства
Случайной величиной называется числовая функция X X( ω ),
заданная на пространстве элементарных событий, для которой при любом действительном x множество {ω: X(ω)≤x} является событием.
Случайные величины обозначают большими латинскими буквами X, Y, Z, … , а возможные значения случайных величин обозначают малыми латинскими буквами x, y, z, … .
Чтобы знать все о случайной величине, надо для любого x знать вероятность P({ω: X(ω)<x})=P(X<x), т.е. совокупность всех таких вероятностей концентрирует все знания о распределении вероятностей по значениям случайной величины.
Значит, в зависимости от природы множества возможных
значений случайной величины, все модели случайных величин можно разделить на два класса – для счетных и несчетных множеств.
Величина X называется дискретной случайной величиной, если множество ее возможных значений представляет собой конечную или бесконечную последовательность чисел x1 , x2 ,…, xn , … и если каждое
событие X ωi xi |
имеет определенную вероятность pi . |
|
|||
Любое правило, позволяющее |
находить |
все |
вероятности |
||
P X ωi xi pi |
называется |
законом |
распределения |
дискретной |
|
случайной величины X. |
|
|
|
|
|
Если составить таблицу, |
в верхней строке |
которой поместить |
|||
возможные значения дискретной случайной величины, а в нижней – соответствующие им вероятности, то такая таблица называется
таблицей распределения или рядом распределения дискретной случайной величины:
75
|
xi |
x1 |
x2 |
|
…. |
|
xn |
… |
|
|
pi |
p1 |
p2 |
|
…. |
|
pn |
… |
|
События X x1, X x2, …, X |
xn , …- несовместны и образуют |
||||||||
|
|
|
|
|
|
|
|
|
|
полную группу. Следовательно, |
pi 1. |
|
|
||||||
|
|
|
|
|
i 1 |
|
|
|
|
Ряд распределения можно |
задать |
графически, если по оси |
|||||||
абсцисс отложить возможные значения случайной величины, а по оси ординат – вероятности этих значений. Соединив последовательно точки
xi ; pi |
отрезками, получим ломаную, которая |
называется |
|
многоугольником распределения вероятностей. |
|
|
|
Для описания закона распределения случайной величины X |
|||
возможен и другой подход: рассматривать не вероятности |
событий |
||
X x |
для разных x, а вероятности события X x , где x – |
текущая |
|
переменная. Вероятность P X x , очевидно, зависит |
от |
x, т.е. |
|
является некоторой функцией от x.
Функция F x P X x , выражающая для каждого x вероятность того, что случайная величина X примет значение, не превосходящее x, называется функцией распределения случайной величины X.
Для дискретной случайной величины X функцию распределения
получают по правилу: F x |
|
P X xi - как «накопленную» |
|
i : xi x |
|
вероятность.
Свойства функции распределения:
1)0 F x 1.
2)P x1 X x2 F x2 - F x1 .
3)F x - неубывающая функция.
4)P X x 1- F x .
5) |
lim F x 1; |
lim F x 0. |
|
x |
x - |
76
6) |
F x - непрерывна слева, т.е. |
lim F x |
x F x . |
|
|
x 0 |
|
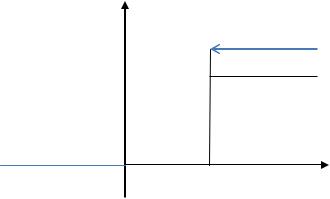
Пример 1.1 Постройте ряд распределения и функцию распределения случайного числа попаданий мячом в корзину при одном броске, если вероятность попадания мячом в корзину при одном броске равна 0,3.
Решение: Обозначим через X - число попаданий мячом в корзину при одном броске. По условию вероятность попадания мячом в корзину при одном броске равна 0,3, следовательно, вероятность непопадания равна 1-0,3=0,7. Ряд распределения:
|
|
xi |
0 |
1 |
|
|
|
pi |
0,7 |
0,3 |
|
Для x 0 |
функция распределения F x P X x 0 ; |
||||
если 0 x 1, то F x 0,7 , если x 1, то F x 0,7 0,3 1.
F(x)
1
0,7 
0 |
1 |
x |
Рис. 6
■
Две случайные величины X и Y называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина.
Рассмотрим две дискретные случайные величины X и Y:
xi |
x1 |
x2 |
… |
xn |
pi |
p1 |
p2 |
… |
pn |
77
|
|
y j |
|
y1 |
|
y2 |
|
… |
|
y k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p j |
|
p1 |
|
p2 |
|
… |
|
pk |
|
|
|
Независимость этих случайных величин означает независимость |
|||||||||||||
событий X xi |
и Y y j , т.е. должно выполняться равенство: |
||||||||||||
|
|
|
P X xi ;Y y j P X xi ·P Y y j . |
|
|||||||||
Произведением kX случайной величины X на постоянную |
|||||||||||||
величину |
k |
называется случайная величина, которая принимает |
|||||||||||
значения kxi с теми же вероятностями pi (i=1, 2, …, n). |
|
||||||||||||
m-й степенью случайной величины |
|
X, т.е. |
X m , |
называется |
|||||||||
случайная |
величина, |
которая |
принимает |
значения |
x m |
с теми же |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
вероятностями pi (i=1, 2, …, n).
Суммой (разностью или произведением) независимых
случайных величин X и Y называется случайная величина, которая принимает все возможные значения вида xi y j ( xi - y j или xi ·y j )
где i=1, 2, …, n; j=1, 2, …, n с вероятностями:
pij P X xi ·P Y y j .
Пример 1.2 Пусть заданы распределения вероятностей независимых случайных величин X, Y и W. Случайная величина W имеет такой же закон распределения, что и Y.
xi |
-1 |
0 |
1 |
2 |
y j |
-1 |
1 |
pi |
0,3 |
0,4 |
0,2 |
0,1 |
p j |
0,6 |
0,4 |
Составьте таблицы распределения для следующих случайных величин: а) Z=X+Y; б) T=Y+W; в) R=2·Y; г) S=X·Y.
Решение: а) Для того, чтобы получить закон распределения случайной величины Z=X+Y составим вспомогательную таблицу, в каждой клетке которой в правом верхнем углу указывается возможное значение
78
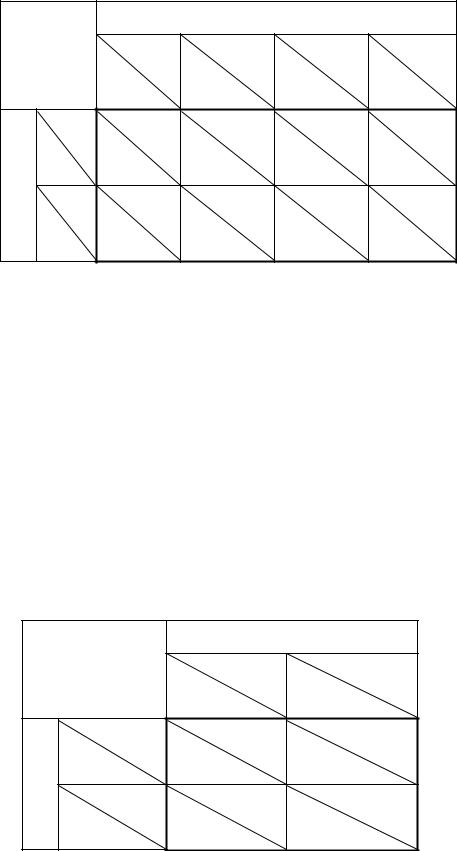
случайной величины, а после наклонной черты - соответствующая ему |
||||||
вероятность: |
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
zi |
-1 |
|
0 |
1 |
2 |
|
|
0,3 |
0,4 |
0,2 |
|
0,1 |
|
-1 |
-2 |
|
-1 |
0 |
1 |
|
0,6 |
0,18 |
0,24 |
0,12 |
|
0,06 |
Y |
1 |
0 |
|
1 |
2 |
3 |
|
|
|||||
|
0,4 |
0,12 |
0,16 |
0,08 |
|
0,04 |
Теперь составим таблицу распределения для случайной величины Z: |
||||||
zi |
-2 |
-1 |
0 |
1 |
2 |
3 |
pi |
0,18 |
0,24 |
0,24 |
0,22 |
0,08 |
0,04 |
Для проверки найдем сумму вероятностей:
6
pi 0,18 0,24 0,24 0,22 0,08 0,04 1. i 1
б) Закон распределения случайной величины T=Y+W получается аналогично: сначала составим вспомогательную таблицу, а затем итоговую:
|
|
|
Y |
ti |
|
-1 |
1 |
|
0,6 |
|
0,4 |
|
-1 |
-2 |
0 |
0,6 |
0,36 |
|
0,24 |
W |
1 |
0 |
2 |
0,4 |
0,24 |
|
0,16 |
79
ti |
-2 |
0 |
2 |
pi |
0,36 |
0,48 |
0,16 |
Для проверки найдем сумму вероятностей: 0,36+0,48+0,16=1.
в) Закон распределения случайной величины R=2·Y составим, пользуясь определением произведения константы на случайную величину:
ri |
-2 |
2 |
pi |
0,6 |
0,4 |
Очевидно, что случайные величины T=Y+W=Y+Y и R=2·Y имеют различные законы распределения.
г) Закон распределения для случайной величины S=X·Y получаем также составляя вспомогательную таблицу, а затем итоговую:
si |
-2 |
-1 |
0 |
1 |
2 |
pi |
0,06 |
0,24 |
0,4 |
0,26 |
0,04 |
Сумма вероятностей:
0,06+0,24+0,4+0,26+0,04=1.
■
Закон распределения дает исчерпывающую характеристику случайной величины, но в ряде случаев не требуется знать весь закон распределения, а достаточно описать его в общих чертах – несколькими числами, отражающими наиболее важные особенности закона распределения. Такого рода числа называют числовыми характеристиками случайной величины (или соответствующего закона распределения). Многие задачи удается решить, оставляя в стороне законы распределения и оперируя только числовыми характеристиками.
80
