Rybleva_teoria veroatnosti_2014

Постройте ряд распределения X - случайного числа испытанных приборов, график ее функции распределения и вычислите математическое ожидание и дисперсию.

1.12 Пусть X – выручка фирмы в $. Найдите распределение выручки в рублях Z=X·Y в пересчете по курсу доллара Y, если выручка не зависит от курса, а распределения X и Y имеют вид:

Найдите среднюю ожидаемую выручку и стандартное отклонение.

1.13 Пусть X – выручка фирмы (в тыс.$), Y – затраты (в тыс.$), Z=X-Y - прибыль. Постройте функцию распределения F z и найдите среднюю ожидаемую прибыль, если выручка и затраты независимы, а их распределения вероятностей заданы таблицами:

91

Ответы:

1.1 35/18. 1.2 5 десятков (при этом средняя выручка равна $45,2);

2.2. Основные законы распределения дискретных случайных величин

РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НА МНОЖЕСТВЕ

Пусть дискретная случайная величина X принимает целочисленные значения от 1 до n с одинаковыми вероятностями

92

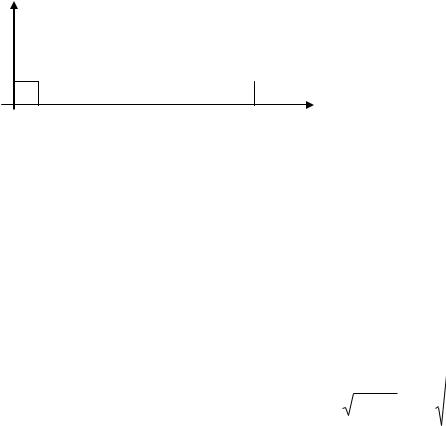
Графически представим данное распределение в виде многоугольника распределения вероятностей:

ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ Пусть ведется стрельба по некоторой цели до первого попадания,

причем вероятность попадания при каждом выстреле не зависит от результатов предыдущих выстрелов и сохраняет постоянное значение p (0<p<1). Число X произведенных выстрелов – случайная величина, возможными значениями которой являются:

1)все натуральные числа (если количество патронов не ограничено);

2)все числа: 1, 2, …, n (если всего n патронов).

Составим ряд распределения и получим числовые характеристики для каждого случая.

Числовые характеристики этой случайной величины:

93

дискретная случайная величина будет иметь следующий ряд распределения:

распределения, если она принимает значения 0, 1, …,m, …, n с вероятностями P X m Cnmpmqn-m .

Биномиальное распределение описывает последовательность независимых испытаний по схеме повторной выборки.

Числовые характеристики случайной величины X, распределѐнной по биномиальному закону:

M X np , D X npq .

ЗАКОН РАСПРЕДЕЛЕНИЯ ПУАССОНА

Дискретная случайная величина X, которая может принимать

В отличие от биномиального распределения здесь случайная величина может принимать бесконечное множество значений, представляющее собой бесконечную последовательность целых чисел 0, 1, 2, …. Закон Пуассона описывает число событий k, происходящих за одинаковые промежутки времени. При этом полагается, что события появляются независимо друг от друга с постоянной средней интенсивностью, которая характеризуется параметром λ np . Так как для распределения Пуассона вероятность p появления события в каждом испытании мала, то это распределение называют законом распределения редких явлений.

95

одинаковой вероятностью p 0,5 , то случайная величина X

подчиняется биномиальному закону распределения. Значит,

i 0

Среднее ожидаемое число появлений герба: M X np 5·0,5 2,5.

■

Пример 2.3 Вероятность попадания в цель при одном выстреле равна 0,015. Сделано 600 выстрелов. Какова вероятность того, что число попаданий в цель не меньше 7 и не больше 10?

Решение: Так как вероятность «успеха» одинаковая и не меняется, испытания независимы и их количество достаточно велико, то случайная величина X (число попаданий) распределена по закону Пуассона. Следовательно, вероятности определяются по формуле:

следует найти вероятность того, что значение случайной величины X попадает в интервал [7,10], т.е. найти вероятность:

P 7 ≤ X ≤ 10 P X 7 P X 8 P X 9 P X 100,1171 0,1318 0,1318 0,1186 0,4993 .

■

Значения вероятностей можно найти по таблице распределения Пуассона при заданных значениях λ и k (в Приложении №3) или с помощью статистической функции:

ПУАССОН(x, среднее, интегральный), где x=k; среднее=λ;

интегральный – логическое значение, определяющее вид функции:

97

ИСТИНА – для вычисления значений функции распределения F x и

ЛОЖЬ – для вычисления вероятности P X k .

Пример 2.4 Из партии, содержащей 100 изделий, среди которых имеется 10 дефектных, выбраны случайным образом 5 изделий для проверки их качества. Построить ряд распределения случайного числа X дефектных изделий, содержащихся в выборке и определить

среднее ожидаемое число брака в выборке и дисперсию.

Решение: Так как изделия выбираются без возвращения, то в данном случае X распределено по гипергеометрическому закону. Значит,

Среднее ожидаемое число бракованных изделий в выборке:

можно в EXCEL с помощью функции ГИПЕРГЕОМЕТ(m,n,M,N).

Пример 2.5 Стороны прямоугольного участка X и Y в результате погрешностей измерения оказываются случайными величинами с такими распределениями:

98

представлено 4 баланса. Составьте закон распределения случайной величины X – числа правильных заключений на проверяемые балансы.

2.5В среднем по 3% договоров страховая компания выплачивает страховую сумму. Найдите вероятность того, что из 100 заключенных договоров с наступлением страхового случая будет связано не более 5- ти договоров. Опишите закон распределения случайной величины X – числа выплат страховой суммы.

2.6Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составьте закон распределения случайной величины X – числа возвращѐнных в срок кредитов из пяти

выданных, постройте график функции распределения, вычислите M X

и σ X .

2.7Разыгрывается лотерея. Выигрыши: машина стоимостью 200 тыс. руб., телевизор стоимостью 50 тыс. руб., пылесос стоимостью 5 тыс. руб. Всего выпущено 10 тыс. билетов, цена одного билета 20 руб. а) Какой будет средняя прибыль человека, купившего один билет? б) Сколько должен стоить билет, чтобы организатор игры получил прибыль в размере 20% от своих затрат? (* Учитываются только затраты на приобретение выигрышей).

2.8Вероятность успешной сдачи экзамена для студента, посещавшего все занятия и выполнявшего все домашние задания по данной дисциплине, равна 0,7; для нерадивого студента – 0,1. Составьте закон распределения числа студентов, успешно сдавших экзамен для четырех человек, выбранных наудачу из совокупности: а) прилежных студентов; б) прогульщиков. Найдите среднее число успешно сдавших экзамен для каждой группы студентов.

2.9Задано распределение дискретной случайной величины X:

100