
Rybleva_teoria veroatnosti_2014
.pdf
Решение: Обозначим через X – рост случайно выбранного мужчины. По условию случайная величина X~N(175;10).
Доля мужчин II роста в данной совокупности равна вероятности:
P 167 |
X 173 F 173 - F 167 |
Ф( |
173 - 175 |
) - Ф( |
167 - 175 |
) |
|
|
|||||
|
|
10 |
|
10 |
|
|
Ф - 0,2 - Ф - 0,8 1- Ф 0,2 - 1 - Ф 0,8 Ф 0,8 - Ф 0,2
0,7881 - 0,5793 0,2088 , т.е. составляет около 20,9%.
P 173 ≤ X ≤ 179 F 179 - F 173 Ф( |
179 - 175 |
) - Ф( |
173 - 175 |
) |
|
||||||
|
|
|
|
|
|||||||
10 |
|
|
10 |
|
|
|
|||||
Ф 0,4 - 1 - Ф 0,2 0,6554 0,5793 - 1 0,2347 , т.е. около 23,5%. |
|
||||||||||
Доля мужчин IV роста составляет: |
|
|
|
|
|
||||||
P 179 ≤ X ≤ 185 F 185 - F 179 Ф( |
185 - 175 |
) - Ф( |
|
179 - 175 |
) |
|
|||||
|
|
|
|||||||||
10 |
|
|
10 |
|
|
|
|||||
Ф 1 - Ф 0,4 0,8413 - 0,6554 0,1859 , т.е. около 18,6%. |
|
||||||||||
Доля тех, кто ниже 167 см., в данном обществе примерно равна: |
|||||||||||
P X 167 F 167 Ф(167 - 175 ) Ф - 0,8 1- Ф 0,8 0,2119 , |
т.е. |
||||||||||
Доля мужчин III роста равна: |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
10
около 21,2%.
Доля мужчин ростом выше 185 см. равна:
P X 185 1- P X 185 1- F 185 1- Ф(185 - 175 ) 1- Ф 1
10
1- 0,8413 0,1587 , т.е. около 16%.
■
Пример 4.4 Пусть доход семьи X в некоторой совокупности имеет равномерное распределение на отрезке от 10 тыс. руб. до 30 тыс. руб. Определите: а) 20% семей с высокими доходами; б) 30% малообеспеченных семей; в) 80% типичных семей со средним уровнем дохода.
Решение: Так как по условию распределение равномерное, то функция плотности распределения вероятностей имеет вид:
121
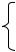
p(x) |
0 при |
x 10, |
x 30 . |
|
|
|
|
1/ 20 |
при 10 x 30 |
|
|
|
|
Функция распределения для 10 x 30 |
равна: F(x) (x - 10)/20 . |
|||||
Задача сводится к отысканию квантиля заданного уровня: |
||||||
|
|
|
F(x p ) |
x p - 10 |
p . |
|
|
|
|
|
|
||
|
|
|
20 |
|
||
|
|
|
|
|
|
|
Для определения 20% семей с высокими доходами надо найти 80% семей с доходами невысокими: x0,8 10 20·0,8 10 16 26 (тыс.
руб.), т.е. семьи с доходом выше 26 тыс. руб. относятся к 20% обеспеченных семей.
30% малообеспеченных семей – это семьи с доходом не выше x0,3 10 20·0,3 16 (тыс. руб.).
Типичные 80% семей – это семьи с доходом от x0,1 10 20·0,1 12 (тыс. руб.) до x0,9 10 20·0,9 28 (тыс. руб.)
■
Задачи для самостоятельного решения:
4.1Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого числа. Полагая, что ошибка округления распределена по равномерному закону, найдите: а) математическое ожидание и стандартное отклонение этой случайной величины; б) вероятность того, что ошибка округления меньше 0,4.
4.2Манометр показывает давление в колонне. Давление колеблется от 10,0 до 10,2 атм., и в этих пределах любое давление равновозможно. Вследствие повреждения манометра его стрелка отклоняется не больше, чем на 10,16 атм. Какое давление в среднем показывает манометр?
4.3Вероятность случайной величины X на отрезке [ 2; 6]
распределена с постоянной плотностью p x c |
для 2 x 6 и |
122

p x 0 для остальных x. Найдите: а) постоянную c; б) матема-
тическое ожидание и стандартное отклонение данной случайной величины; в) функцию распределения; г) вероятности событий P X 1
, P 3 X 5 и P X 5 .
4.4Стержень ломают в случайной точке. Какова средняя длина наименьшего куска?
4.5Случайная величина X задана функцией распределения:
F x |
0 при x 0 |
|
|
1 - e-0,4x при x |
0 |
||
|
Найдите математическое ожидание и стандартное отклонение случайной величины, вероятность P 2 X 5 .
4.6Плотность вероятности случайной величины X имеет вид:
p x |
0 при x 0 |
. Найдите параметр c. |
c·e-0,1x при x 0 |
4.7На предприятии утреннее совещание обычно продолжается около часа. Однако в этот раз часа не хватило. Какова вероятность, что совещание продлится еще не меньше 15 мин.?
4.8Установлено, что время ремонта электроплит есть случайная величина X, распределенная по показательному закону. Определите вероятность того, что на ремонт электроплиты потребуется не менее 20 дней, если среднее время ремонта составляет 15 дней. Найдите функцию плотности, функцию распределения и стандартное отклонение величины X.
4.9Для функции плотности распределения случайной величины, подчиняющейся нормальному закону с параметрами a и σ, найдите: асимптоты, промежутки возрастания и убывания, экстремум функции, промежутки выпуклости и точки перегиба. Нарисуйте эскиз графика – кривую Гаусса.
4.10Средняя дневная выручка магазина равна 100 тыс. руб., стандартное отклонение 20 тыс. руб. Следует ли считать значение
123
дневной выручки x1 50 тыс. руб. подозрительно малым, а значение x2 170 тыс. руб. подозрительно большим?
4.11Среднее суточное потребление хлеба в некоторой совокупности, объем которой 100 тыс. человек, составляет 300 гр., стандартное отклонение 50 гр. Определите запас хлеба, который покрывает суточную потребность с вероятностью 0,95.
4.12Предположим, что средний суточный спрос на мясо в городе составляет 20 т., стандартное отклонение – 3 т. Среднее предложение равно 22 т., стандартное отклонение предложения равно 4 т. Какова вероятность того, что спрос превысит предложение? Как следует изменить среднее предложение, чтобы спрос удовлетворялся с вероятностью 0,99?
4.13Средний срок службы прибора равен 100 часов, стандартное отклонение 20 часов. Фирма платит штраф 300 тыс. руб., если прибор проработает менее 50 часов. Найдите ожидаемый размер штрафа для партии 200 приборов.
Ответы: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
4.1 M(X)=0,5; σ 0,295 ; |
P 0,4. |
4.2 |
10,8. 4.3 |
c=1/4; |
M(X)=4; |
||||||||||
σ 2 / |
|
; |
|
|
|
|
L |
. |
|
|
|
||||
3 |
P(X≤1)=0; P(X>5)=1/4; |
P(3<X≤5)=1/2. |
4.4 |
|
4.5 |
||||||||||
|
4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M(X)=2,5; |
σ 2,5 ; P(2<X<5)≈0,314. 4.6 |
c=-0,1. 4.7 |
λ |
1 |
. 4.8 |
λ |
|
1 |
; |
||||||
60 |
15 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
σ 15 ; P X 20 0,28 . 4.12 |
P 0,3446 ; |
a 31,65 . |
4.13 |
372000. |
|
|
|
||||||||
124

2.5. Многомерные случайные величины
На одном и том же пространстве элементарных событий может быть определена не одна, а несколько случайных величин. Необходимость в этом возникает, например, при моделировании ситуации, когда объект характеризуется несколькими случайными параметрами. Например, предприятие можно описать с помощью нескольких случайных величин: X1 - объѐм продукции, выпускаемой за день; X 2 - количество работающих на предприятии; X 3 - ассортимент продукции; X 4 - рентабельность производства и т.д.
Пусть X1, X2, ... , Xn - случайные величины, определенные на множестве элементарных событий Ω . Удобно рассматривать их как координаты n-мерного случайного вектора X X1, X2, ... , Xn .
Под n-мерной случайной величиной, или случайным вектором,
понимается |
упорядоченный |
набор |
n |
случайных |
величин |
||
|
|
X1, X2, ... , Xn . Случайные величины |
|
могут быть |
|||
X |
X1, X2, ... , Xn |
||||||
как дискретными, так и непрерывными. |
|
|
|
||||
На многомерные случайные величины распространяются почти без изменений основные определения, относящиеся к одномерным
случайным величинам. |
|
|
|
||
|
|
|
F |
|
n-мерной случайной величины |
|
|
Функция распределения |
X |
||
|
|
X1, X2, ... , Xn определяется формулой: |
|||
X |
|||||
|
|
F X1, X2, ... , Xn P ω : |
X1 ω x1, X2 ω x2, ... , Xn ω xn |
||
Функция - неубывающая функция каждого аргумента и определяет закон распределения случайной величины X .
Рассмотрим двумерные случайные величины. Для случайной
величины X , Y |
функция распределения |
F x, y определяется |
следующим образом: F x, y P X x, Y y . |
|
|
125
Свойства функции распределения двумерной случайной величины:
1. Функция распределения FXY x, y есть неотрицательная функция, заключѐнная между нулѐм и единицей: 0 FXY x, y 1.
2.Функция распределения FXY x, y есть неубывающая функция
по каждому из аргументов:
при |
x2 x1 |
FXY x2, y |
FXY x1, y , |
при |
y2 y1 |
FXY x, y2 |
FXY x, y1 . |
3.FXY x, FXY , y FXY , 0 ,
где, например, F |
x, lim |
F |
x, y . |
XY |
y |
XY |
|
4.Если один из аргументов стремится к , то функция
распределения FXY x, y становится равной функции распределения случайной величины, соответствующей другому аргументу:
FXY x, FX x P X x ,
FXY , y FY y P Y y .
5. Если оба аргумента стремятся |
к , то функция |
распределения FXY x, y равна единице: |
F , 1. |
Геометрически функция распределения есть некоторая поверхность, обладающая указанными свойствами. Для дискретной случайной двумерной величины еѐ функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции FXY x, y . Зная функцию распределения, можно найти вероятность попадания случайной точ-
ки X , Y в пределы прямоугольника:
P x1 X x2 , y1 Y y2 F x2 ,y2 F x1,y2 F x2 ,y1 F x1,y1
Условным законом распределения одной из одномерных составляющих двумерной случайной величины X , Y называется еѐ
126

закон распределения, вычисленный при условии, что другая составляющая приняла определѐнное значение (или попала в какой-то
интервал). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
дискретную |
|
случайную |
|
величину |
|
X , Y , закон |
||||||||||||||||
распределения которой задан таблицей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
X |
x1 |
|
|
|
|
x2 |
|
|
|
|
… |
|
|
|
|
|
|
xn |
|
||||
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y1 |
p11 |
|
|
|
|
p12 |
|
|
|
|
… |
|
|
|
|
|
|
p1n |
|
||||
|
y2 |
p21 |
|
|
|
|
p22 |
|
|
|
|
… |
|
|
|
|
|
|
p2n |
|
||||
|
: |
: |
|
|
|
: |
|
|
|
|
|
|
: |
|
|
|
|
|
|
: |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y m |
pm1 |
|
|
|
|
pm2 |
|
|
|
|
… |
|
|
|
|
|
|
pmn |
|
||||
|
Условные распределения определяются следующим образом: |
|||||||||||||||||||||||
|
P X xi /Y y j |
|
|
x |
, Y y |
|
|
|
|
|
p |
|
|
|
||||||||||
|
|
P X |
j |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
ij |
|
, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|||||||||||||
|
|
|
|
|
|
|
P Y y j |
|
|
|
|
|
|
|
|
pij |
|
|
|
|||||
|
|
|
|
|
|
P X xi |
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|||||
|
|
|
|
|
, Y y j |
|
|
|
pij |
|
|
|
||||||||||||
|
P Y y j / X xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
||
|
|
|
|
P X xi |
|
|
|
|
|
m |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pij |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
||
|
n |
|
|
|
|
|
|
|
m |
|
|
|
y j / X xi 1. |
|||||||||||
при этом: P X xi /Y y j 1 |
и |
P Y |
||||||||||||||||||||||
|
i 1 |
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Важной характеристикой условного распределения вероятностей является условное математическое ожидание.
Условным математическим ожиданием дискретной случайной величины X при Y y j называют произведение возможных значений
X на их условные вероятности:
M X /Y y j n xi P X xi /Y y j .
i 1
127
Аналогично определяется условное математическое ожидание Y при
|
M Y / X xi |
m |
|
|
|
X xi : |
y j P Y y j / X xi . |
|
|||
|
|
|
j 1 |
|
|
Условное математическое ожидание |
M X /Y y j |
называют |
|||
функцией |
регрессии |
X |
на Y , |
соответственно |
условное |
математическое ожидание |
M X /Y y j - функцией регрессии Y на |
||||
X . |
|
|
|
|
|
Теорема. |
Для того чтобы |
случайные |
величины X и |
Y были |
|
независимыми, необходимо и достаточно, чтобы функция распределения двумерной случайной величины X , Y была равна произведению функций распределения составляющих:
FXY x, y FX x FY y .
Это значит, что P X x, Y y P X x P Y y .
Если же случайные величины X и Y зависимы, то для оценки тесноты взаимосвязи используют коэффициент корреляции, который вычисляют по формуле:
rXY |
cov X , Y |
|
|
M X Y M X M Y |
, |
||
|
|
|
|
||||
σ X σ Y |
σ X σ Y |
||||||
|
|
|
|||||
где математическое ожидание произведения вычисляется по формуле:
M X Y |
n m |
|
|
|
|
|
|
xi y j pij . |
|
|
|
||||
|
i 1j 1 |
|
|
|
|
|
|
Свойства коэффициента корреляции случайных величин |
|||||||
аналогичны свойствам |
коэффициента корреляции для |
случайных |
|||||
|
|
|
|
|
|||
событий (см. стр. 60). |
Чем ближе значение |
rXY |
к 1, тем сильнее |
||||
|
|
||||||
взаимосвязь между случайными величинами X и Y ; чем ближе |
rXY |
|
|||||
к 0, тем слабее взаимосвязь. |
|
|
|
||||
Для |
независимых случайных величин X и Y : rXY 0 и такие |
||||||
случайные |
величины |
называются некоррелированными. |
X и Y |
||||
называют коррелированными, если rXY 0 . |
|
|
|
||||
|
|
128 |
|
|
|
|
|

Коэффициент корреляции характеризует тесноту линейной зависимости. Следовательно, для зависимых случайных величин X и Y может быть rXY 0 , но может и равняться нулю: rXY 0 .
Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости ещѐ не вытекает коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности ещѐ нельзя заключить независимость этих величин. Однако для нормально распределѐнных случайных величин из некоррелированности вытекает их независимость.
Пример 5.1 Задана таблица распределения дискретной двумерной случайной величины:
|
|
X |
1 |
2 |
|
3 |
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0,12 |
0,12 |
|
0,08 |
|
|
|
|
|
|
|
|
|
|
|
1 |
0,28 |
0,13 |
|
0,27 |
|
|
|
|
|
|
|
|
|
а) |
найти законы распределения случайных величин X и Y ; |
||||||
б) найти условный закон распределения Y при условии, что X 2 ; |
|||||||
в) найти условный закон распределения X при условии, что Y 1; |
|||||||
г) |
вычислить числовые характеристики для X |
и Y (математические |
|||||
ожидания и стандартные отклонения); д) установить, зависимы или нет X и Y .
Решение: а) случайная величина Y принимает два значения: y1 1 и y2 1. Вероятности этих значений соответственно равны:
p1 p11 p12 p13 |
0,12 0,12 0,08 0,32 , |
|
p2 p21 p22 p23 |
0,28 0,13 0,27 0,68 . Аналогично |
получаем |
вероятности значений для случайной величины X : p1 0,4 , |
p2 0,25 и |
|
p3 0,35 . Следовательно, законы распределения случайных величин
129
(т.е. безусловные законы распределения X и Y ) можно представить в виде:
xi |
1 |
2 |
3 |
pi |
0,4 |
0,25 |
0,35 |
y i |
-1 |
1 |
pi |
0,32 |
0,68 |
б) Найдѐм условные вероятности Y при условии, что X 2 : |
|
||||||||||||||||||||||||||
P Y 1/ X 2 |
0,12 |
|
|
12 |
0,48 ; P Y 1/ X 2 |
|
0,13 |
|
13 |
0,52 . |
|||||||||||||||||
|
|
|
|
|
|
0,25 |
25 |
||||||||||||||||||||
|
0,25 |
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Проверка: 0,48 0,52 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
в) Условные вероятности X при условии, что Y 1: |
|
|
|
||||||||||||||||||||||||
P X 1/Y 1 |
0,28 |
|
|
28 |
; |
P X 2 /Y 1 |
0,13 |
|
|
13 |
; |
|
|
|
|||||||||||||
0,68 |
|
68 |
|
|
68 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
0,68 |
|
|
|
|
|
|
|||||||||||||
P X 3 /Y 1 |
|
0,27 |
|
|
27 |
. |
Проверка: |
28 |
|
13 |
|
27 |
|
1. |
|
|
|
||||||||||
0,68 |
68 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
68 |
68 |
68 |
|
|
|
|
|
|
|
|
|||||||||||||
г) M X 1 0,4 2 0,25 3 0,35 1,95 ;
M X 2 0,4 1 3,15 4,55 ;
D X 4,55 3,8025 0,7475 ; |
σ X 0,865 . |
M Y 1 0,32 1 0,68 0,36 ; M Y 2 0,32 0,68 1; |
|
D Y 1 0,1296 0,8704 ; |
σ Y 0,933 . |
д) Выясним, зависимы или нет рассматриваемые случайные величины (см. теорему о независимости). Проверим, например, будет ли выполняться равенство: FXY 2,5; 0 FX 2,5 FY 0 , т.е. будет ли верно следующее равенство P X 2,5;Y 0 P X 2,5 P Y 0 ?
FXY 2,5; 0 P X 2,5;Y 0 0,12 0,12 0,24 . |
|
|
FX 2,5 P X 2,5 0,4 0,25 0,65 ; |
FY 0 P Y 0 0,32 . |
=> |
FX 2,5 FY 0 0,208 .
Получили: 0,24 0,208 => случайные величины X и Y - зависимы. *Замечание. Можно было проверить выполняется ли равенство:
pij P X xi P Y y j ?
130
