Rybleva_teoria veroatnosti_2014

Пример 3.5 Определить вероятность того, что в группе из 20-ти человек имеются совпадающие дни рождения.

Решение: Обозначим через А искомое событие, тогда противоположное ему событие A означает, что совпадающих дней рождения нет. Число

всех элементарных исходов опыта равно 36520 , а число исходов,

Тогда P A 1- P A 1- 0,589 0,411.

■

Одним из недостатков модели Лапласа (классического определения вероятности) является предположение о конечном числе возможных исходов испытания. Но часто встречаются такие испытания, для которых число возможных исходов бесконечно.

Втаких случаях строится геометрическая модель:

рассматривается пространство Ω с бесконечным числом равновозможных исходов. Элементарные исходы интерпретируются как выбор наудачу точки из некоторого множества в Rm . Предполагается, что множество имеет некоторую геометрическую форму, которую можно каким-либо образом измерить (определить длину – в R1, либо вычислить площадь – в R2 , объем – в R3 и т.п.). Событием называется следующее: выбранная точка принадлежит заданной части фигуры. Вероятность такого события определяется как отношение меры (обозначение mes) части фигуры А к мере всей фигуры Ω:

P A mes A . mes Ω

В описанной геометрической модели остаются в силе все аксиомы А.1 – А.3, соответственно выполняются все свойства 1 – 5.

31

Пример 3.6 Пусть отрезок l составляет часть отрезка L. Определить вероятность попадания точки, поставленной наугад, на отрезок l. Решение: В результате данного опыта (бросания наугад точки) возможно бесчисленное множество исходов: при этом нет оснований считать неравновозможными хотя бы два каких-либо исхода из всего множества исходов.

Понятно, что брошенная точка может оказаться на отрезке l (l 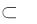L), а может там и не оказаться. Поэтому возможно говорить о вероятности попадания точки на отрезок l. В данном случае мерой рассматриваемых множеств является длина:

mes( l )=длина l, mes( L )=длина L.

Тогда: P A Ll .

■

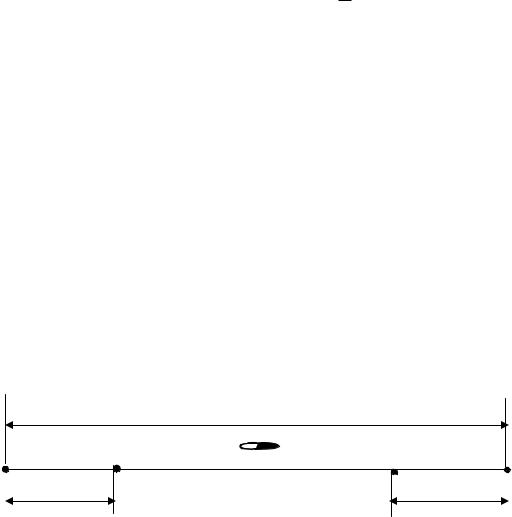
Пример 3.7 Перед окопами вдоль прямой линии через каждые 10 метров установлены противотанковые мины. Перпендикулярно этой линии движется танк, ширина которого 3 метра. Какова вероятность того, что танк пересечет линию установки мин невредимым?

Решение: Ось симметрии танка может пересечь линию установки мин в любой ее точке, т.е. исходы испытания (пересечения линии) образуют бесконечное множество, поэтому здесь классическое определение вероятности неприменимо. Пусть отрезок прямой, расположенный между двумя соседними минами, изображен на рис.2. Танк при своем движении может попасть на один из таких отрезков.

10м

32

танка попадет на отрезок АС или DB, то произойдет взрыв, а если ось симметрии попадет на отрезок CD, то его не будет. Таким образом, областью, благоприятствующей наступлению события А, заключающегося в беспрепятственном пересечении линии установки мин, является отрезок CD, а множеству всех исходов соответствует отрезок АВ. Тогда вероятность благополучного продвижения танка

Пример 3.8 Пассажир может добраться до места на любом из двух автобусов, интервалы движения которых соответственно равны 5 и 10 мин. Определить вероятность того, что пассажиру, подошедшему в случайный момент времени на остановку, ждать придется не более 2

можно рассматривать как координаты точки на плоскости. Все пространство возможных элементарных исходов можно описать как множество Ω={(x;y): 0≤x≤5, 0≤y≤10}, а искомое событие А как часть этого множества (на рис.3 прямоугольник изображает множество Ω, а заштрихованная фигура – множество А):

■

33

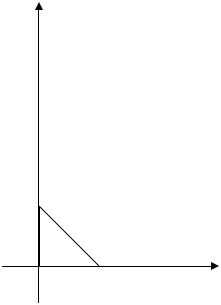
Пример 3.9 Пассажир может добраться до места с пересадкой на двух автобусах, интервалы движения которых соответственно равны 5 и 10 мин. Вычислить вероятность того, что на ожидание автобусов пассажиру потребуется не более 2 мин.

Решение: Условие данной задачи отличается от предыдущей тем, что теперь пассажир должен ждать и первый автобус (на одной остановке), и второй автобус (на следующей остановке), т.е. речь идѐт уже о суммарном времени ожидания.

Поэтому все множество элементарных исходов останется прежним, а множество, задающее искомое событие, будет другим: A={(x;y): 0≤x≤5, 0≤y≤10, 0≤x+y≤2 }.

Пример 3.10 (задача о встрече). Два лица (А и В) имеют одинаковую вероятность прийти к указанному месту в любой момент промежутка времени T. Определить вероятность того, что время ожидания одним другого будет не больше t.

Решение: Обозначим моменты прихода к указанному месту лиц А и В соответственно через x и y. По условию 0 ≤ x ≤ T, 0 ≤ y ≤ T. Этим неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату со стороной, равной T. Событие А – встреча двух лиц – произойдет, если разность между x и y не будет превышать величины t,

34

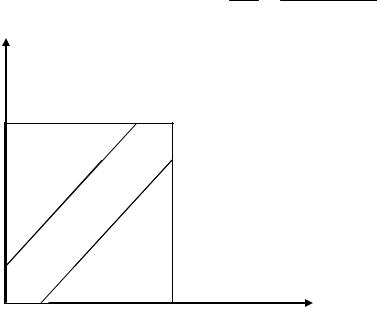
т.е. будет выполняться неравенство |x-y|≤t. Этому неравенству удовлетворяют все точки, лежащие в полосе

x-t ≤ y ≤ x+t, которая на рис. 5 – заштрихована и является частью фигуры Ω.

Тогда вероятность встречи в течение промежутка времени t равна:

«высоковероятные» и «типичные». Интуитивно понятно: если известно, что данное событие имеет вероятность, близкую к нулю, то, скорее всего, в единичном испытании оно не произойдет. Если же вероятность события близка к единице, то практически можно считать, что в единичном испытании это событие наступит.

Естественно возникает вопрос о значении порогового уровня для слишком малой и слишком большой вероятности. Экономисты традиционно в качестве порогового значения, отделяющего «малые»

35

1 α 0,95. Соответственно, если вероятность случайного события А удовлетворяет условию: 0,05 ≤P A ≤0,95 , то такое событие считается

«типичным», следовательно, его наступление в эксперименте можно объяснить случайностью. Если вероятность случайного события А меньше 0,05, но, тем не менее, событие произошло, то это можно считать подозрительным фактом; аналогично подозрительным будет и ненаступление «высоковероятного» события.

Задачи для самостоятельного решения:

3.1Имеются карточки, на каждой из которых – цифра (от 0 до 9). Чему равна вероятность, извлекая наудачу 3 карточки, получить число 129? а) выборка без возвращения; б) с возвращением.

3.2Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь: а) все грани неокрашенные; б) одну окрашенную грань; в) две окрашенные грани; г) три окрашенные грани; д) четыре окрашенные грани.

3.3В коробке лежат одинаковые по внешнему виду конфеты: 2 с орешками и 2 с мармеладом. Возьмем наудачу 2 конфетки. Вероятность какого из событий больше: того, что обе конфеты с одинаковой начинкой или что с разной?

3.4Бросаются два игральных кубика. Какова вероятность того, что: а) сумма выпавших очков равна 7; б) сумма выпавших очков меньше 4; в) сумма равна 7, а произведение не превосходит 10?

3.5Можно ли объяснить случайностью, что в наудачу составленной стопке из 10-ти дисков оказались рядом: а) два определенных диска; б) три определенных диска?

36

3.6Можно ли объяснить случайностью, что в группе из 5 человек, у всех совпадают дни рождения?

3.7Из колоды карт (52 шт.) вынимаются наудачу 4 карты. Какова вероятность того, что они: а) одной масти; б) одного значения; в) все разных значений; г) все разных мастей?

3.8В ящике 5 красных и 8 белых шаров. Наудачу извлекается 3 шара. Какова вероятность того, что среди них: а) ровно 1 белый шар; б) ни одного белого; в) все шары – белые; г) красных больше, чем белых?

3.9Светофор горит 60 сек. зеленым светом и по 30 сек. – красным и желтым. Какова вероятность того, что случайной машине:

а) не придется ждать у светофора; б) придется ждать более 20 сек.? (ехать можно только на зеленый свет).

3.10Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода один час, а второго – два часа.

3.11Два приятеля договорились встретиться между 17 и 18 часами. Каждый приходит наугад и ждет 10 минут. Какова вероятность встречи?

3.12Считают, что дневная выручка магазина X принимает значения от

20 тыс. руб. до 80 тыс. руб. Найти вероятности событий:

А – выручка магазина за один день больше 40 тыс. руб.; B – выручка магазина за два дня больше 80 тыс. руб.; C – выручка магазина за три дня больше 120 тыс. руб.

3.13На дно колодца квадратного сечения поставим ведро, стенки которого касаются стенок колодца. Какова вероятность того, что, бросая наугад камешек, мы попадем в ведро?

3.14В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью T. Моменты поступления сигналов

независимы один от другого. Сигнализатор срабатывает, если разность

37

между моментами поступления сигналов меньше t (t<T). Найти вероятность того, что сигнализатор сработает за время T, если каждое из устройств пошлет по одному сигналу.

3.15 Какова вероятность того, что сумма двух взятых наугад положительных чисел, каждое из которых меньше либо равно единицы,

не превзойдѐт 1, а их произведение будет меньше либо равно 29 ?

3.16Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найти вероятность того, что произведение xy будет не больше единицы, а частное x/y не больше двух.

3.17Наудачу взяты два положительных числа x и y, каждое из которых не превышает единицы. Найти вероятность того, что сумма x+y не превышает единицы, а произведение xy не меньше 0,09.

3.18Код домофона состоит из восьми цифр, которые могут повторяться. Какова вероятность того, что, случайно набирая цифры, можно угадать нужный код?

3.19Двое друзей, Алексей и Вадим, стоят в очереди из 8 человек. Найти вероятность того, что: а) Алексей и Вадим стоят рядом; б) между Алексеем и Вадимом стоят два человека.

3.20Из колоды в 36 карт извлекаются наудачу 4 карты. Какова вероятность событий: A – все извлеченные карты пиковой масти, B – среди этих четырех карт окажется хотя бы один король?

3.21Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Найти вероятность того, что среди трѐх наугад выбранных вопросов студент знает: а) 3 вопроса; б) 2 вопроса; в) 1 вопрос.

3.22Сколько раз нужно бросить игральную кость, чтобы с вероятностью 0,6 хотя бы один раз выпало 6 очков?

3.23В лотерее разыгрывается 100 билетов. Выигрыши выпали на 20 билетов. Некто приобрел 5 билетов. Найти вероятности следующих событий: а) выигрыш выпадет на все 5 билетов; б) выигрыш выпадет хотя бы на один билет; в) выигрыш выпадет на два билета.

38

3.24В ящике 20 деталей, 4 из них – нестандартные. Какова вероятность того, что среди 6 наугад взятых деталей нестандартных не окажется?

3.25Найти вероятность того, что 30 студентов одной группы родились: а) в разные дни года (в году 365 дней); б) в один день года; в) 8 марта; г) в разные месяцы года; д) в сентябре; е) в разные дни сентября.

3.26Какова вероятность того, что произвольно взятое трѐхзначное число делится на 3?

3.27Какова вероятность, что два определенных студента будут направлены на практику в город C, если в наличие имеется 5 мест в город A, 8 – в город B и 7 – в город C?

3.28В круг радиуса r наудачу брошена точка. Какова вероятность того, что эта точка окажется внутри вписанного в круг правильного треугольника?

3.29На отрезке 0; 3 наудачу выбраны два числа x и y . Найти

вероятность того, что эти числа удовлетворяют неравенствам x2 3y 3x .

3.30 Наудачу выбирают два числа из промежутка 0 ; 1 . Какова

вероятность того, что их сумма заключена между 1 и 1?

4 3.31 Дано шесть карточек с буквами Н, М, И, Я, Л, О. Найти вероятность

того, что: а) получится слово ЛОМ, если наугад одна за другой выбираются три карточки; б) получится слово МОЛНИЯ, если наугад одна за другой выбираются шесть карточек и располагаются в ряд в порядке появления.

Ответы:

3.1 а) 0,0014; б) 0,001. 3.2 а) 0,512; б) 0,384; в) 0,096; г) 0,008; д) 0.

3.3 с разной – больше. 3.4 а) ≈0,167; б) 0,083; в) 0,111. 3.5 а) p=0,2; да;

б) p=0,067; нет. 3.6 нет. 3.7 а) 0,01; б) 0,000048; в) 0,676; г) 0,315. 3.8 а)

39

0,28; б) 0,035; в) 0,196; г) 0,315. 3.9 а) 0,5; б) 0,33. 3.10 0,121. 3.11

3.31а) 1/120; б) 1/720.

1.4.Условная вероятность, зависимость и независимость

событий. Формула Байеса

При совместном рассмотрении двух случайных событий A и B часто возникает вопрос: насколько связаны эти события друг с другом, в какой мере наступление одного из них влияет на возможность наступления другого?

Для характеристики зависимости одних событий от других вводится понятие условной вероятности. Пусть P A ≠0, тогда

P AB

отношение называется условной вероятностью события В

P A

при условии наступления события А. Такая вероятность обозначается P(B/A). По определению имеем следующее равенство:

P AB P (B/A) = P A .

Теорема 1 (умножения вероятностей). Вероятность совместного наступления двух событий равна вероятности одного из этих событий при условии другого, умноженной на вероятность самого условия:

P AB P A P B / A .

40