Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тюменский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Rybleva_teoria veroatnosti_2014

.pdf

Скачиваний:

113

Добавлен:

23.03.2016

Размер:

5.58 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2412 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

3.2 а) да; б) да; в) нет; г) да; д) нет; е) нет. 3.3 а) да; б) нет; в) нет; г)

нет. 3.4

M X 1 0,76;

142,26. 3.5 c

;

F x

arctg x

;

x 2

; M X M M 0 . 3.6

p x

2σ 2 .

σ 2

3.7M(X)=0.

2.4.Основные законы распределения непрерывных случайных

величин

РАВНОМЕРНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Непрерывная случайная величина X распределена равномерно на отрезке [ a; b], если все ее возможные значения сосредоточены на этом отрезке и ее плотность распределения на этом интервале постоянна:

p x	c,	a x b
	0,	x a,	x b

p x

b - a

Рис. 10

Найдем постоянную c из условия нормировки:

p x dx 1

p x dx

p x dx 0

dx c· x

b c· b - a => c

c·

b - a

Если x1; x2

a;b , то:

P x X x

p x dx

·x2 dx

x2 - x1

b - a

111

т.е. вероятность попадания в интервал x1; x2 равна отношению длины этого интервала к длине всего отрезка [ a; b].

Тогда функция распределения имеет вид:

	0,		при	x a
F x	x - a	,	при	a ≤ x b

	b - a
	1,		при	x ≥ b

F x

0 a b x Рис. 11

Математическое ожидание равномерно распределенной величины

- a

M X

xp x dx

xdx

(

)

b - a

b - a a

b - a

2(b - a)

M X a b .

Итак, математическое ожидание случайной величины X совпадает с серединой отрезка [ a; b]. Так как распределение симметричное, то медиана также находится в середине отрезка. Дисперсия равна:

D X	1	b		a b	)2dx	1		a b	)3	b	(b - a)	2

			(x -				(x -						.

	b - a a		2			3(b - a)	2			a	12

Стандартное отклонение: σ X b2 - 3a .

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению.

112

ПОКАЗАТЕЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром λ, если ее

плотность вероятности равна:

p x	0 при x 0
	λ·e- λx при x ≥ 0 .

Кривая распределения имеет вид: p(x)

	0	x Рис. 12
	Функция распределения при x 0	равна нулю: F x 0 , а для
x 0	получаем: F X 1 e λx .

График функции распределения имеет вид:

F(x)

Рис. 13

Математическое ожидание равно:

M X

xp x dx

lim xλe- λxdx

lim (-

xde - λx )

b 0

(-xe- λx

e- λxdx)

- λb -

e- λx

b )

lim

lim (-be

Дисперсию определим по формуле: D X M X 2 - M2 X .

113

Для этого сначала найдем начальный момент второго порядка:

x2p x

M X 2

lim x2λe- λxdx

lim

x2de- λx )

b 0

lim (-x 2 e- λx

2 bxe- λxdx) lim

(-b2e- λb )

lim

eλx

λ b 0

M X 2 0

Отсюда D X

λ2

λ λ

λ2

Стандартное отклонение равно: σ X

D X

1/ λ и совпадает с

математическим ожиданием.

Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности. Так, например, интервал времени T между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром λ – интенсивностью потока. При этом, если промежуток времени T уже длился некоторое время t , то это никак не влияет на закон распределения оставшейся части T1 T - t промежутка.

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Непрерывная случайная величина X подчиняется нормальному закону распределения (закону Гаусса) с параметрами a и σ , если ее

плотность вероятности имеет вид:

				1		x -a		2
p(x)	1	-			(		)
	1	-		2	(	σ	)
			e					.

	σ 2π
	σ 2π

Нормальное распределение является одним из наиболее часто встречающихся распределений: рост, вес человека, ошибки измерения, параметры технологических процессов и т.д. подчиняются нормальному закону. Если случайная величина X имеет нормальное распределение вероятностей с параметрами a и σ, то коротко это записывают так:

X~N(a,σ).

114

p x

Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях.

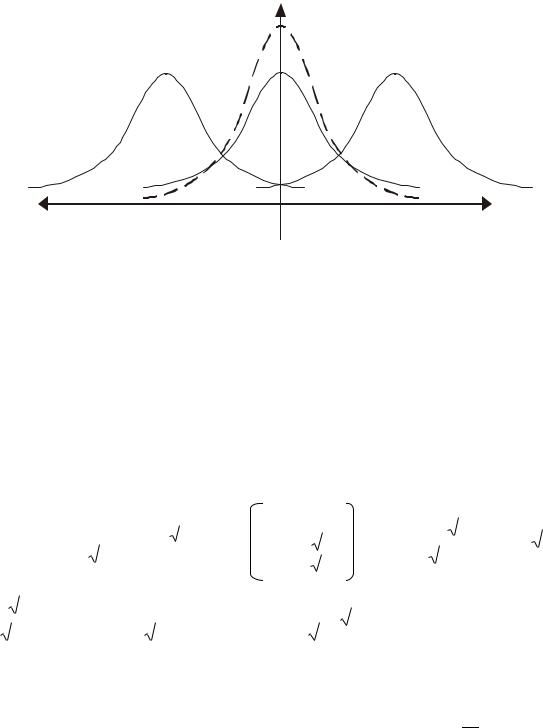
Кривую нормального закона распределения называют нормальной или кривой Гаусса. На рисунке ниже приведено

семейство нормальных кривых в зависимости от параметров a и σ: p x

a<0

a>0

x Рис.14

С геометрической точки зрения параметр a – точка максимума плотности, а также центр симметрии. При увеличении a график смещается вправо, при уменьшении a – влево. При уменьшении σ максимум плотности увеличивается, при этом «хвосты» нормальной кривой «прижимаются» ближе к оси абсцисс.

Выясним теоретико-вероятностный смысл параметров. Математическое ожидание случайной величины X:

x -

x - a

M X

a σ 2t

e-t 2

σ 2

σ 2π

dx σ

σ 2π

2dt

σ 2

te-t 2 dt

e-t 2 dt 0

π -

(первый интеграл равен нулю как интеграл от нечетной функции по симметричному относительно начала координат промежутку, а второй интеграл – это интеграл Эйлера –Пуассона, он равен 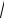π .

115

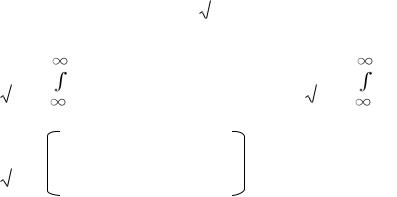
Найдем теперь дисперсию снова применяя замену t (x - a)/σ

D X M X - M X 2

(x -

2π

σ 2

x - a

)2e-

(

x -a

)2 d(

x - a

)

(

2π -

нормальной случайной величины, и интегрируя по частям:

			1		x -a			2
-				(		)			dx
-				(		)
a)2 e			2		σ
	σ 2						-		t 2
	σ 2				t 2e		-		2 dt


		2π -
		2π -

- e-

t 2

2 dt σ2 .

2 t

2π

Таким образом, σ 2 - это дисперсия, σ - стандартное отклонение. Случайная величина называется центрированной, если ее

математическое ожидание равно нулю. Для того чтобы центрировать

случайную величину, надо вычесть из нее математическое ожидание:

M X - M X M X - M X 0.

Случайная величина называется нормированной, если ее

дисперсия равна единице. Для того чтобы нормировать случайную величину, надо поделить ее на стандартное отклонение:

	X	1	D X	σ 2	1.
D
		σ 2		σ 2
	σ

Центрированная и нормированная случайная величина называется стандартной (или стандартизированной). Для того чтобы стандартизировать случайную величину, надо вычесть из нее математическое ожидание и поделить на среднее квадратическое отклонение. Стандартные случайные величины обозначаются большой

латинской буквой Z:	Z	X - a	.

		σ

Так как для нормального распределения M X a и σ X σ , то

116

стандартная случайная величина								Z X - a	~ N(0; 1), т.е. плотность
								σ
		φ z			1	-	z2
имеет вид:					1	-	2 . Функция φ z		- четная, ее значения для
имеет вид:						e	2 . Функция φ z		- четная, ее значения для
				σ	2π
положительных аргументов приведены в Приложении 1.
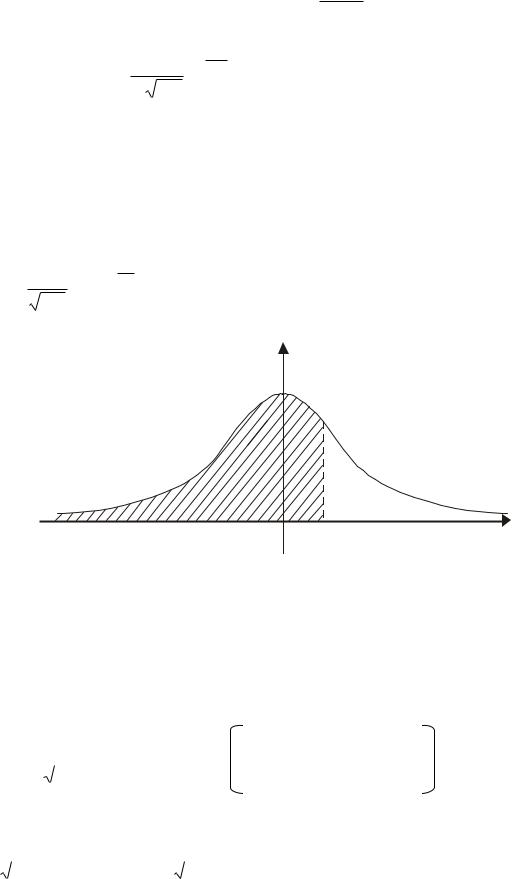
Функция распределения стандартной случайной величины Ф z
равна площади фигуры, ограниченной сверху графиком функции φ z ,
снизу -	осью абсцисс,					а справа -		прямой,	проходящей через точку z:
Ф z	1	z	-	t 2
		z
		e		2 dt		называется функцией Лапласа.
	2π	e		2 dt		называется функцией Лапласа.
	2π	-
							φ z
							0	z	z Рис.15
Для вычисления отрицательного аргумента используется
формула:							Ф - z 1- Ф z .
Функцию распределения случайной величины X~N(a,σ) можно
выразить через Ф z , значения которой можно найти в таблицах (в
данном пособии они приводятся в Приложении 2):

F x

(

t -a

t - a

dt / σ =

σ 2π -

dt σdy

x -a

y 2

x -a

y 2

x - a

) Ф z .

2 σdy

Ф(

2 dy

σ 2π

2π

Иногда табулируются значения функции:

117

1	z		-	t 2		z ,
1	z		-	2 dt Ф
		e			0


2π 0
2π 0

у которой нижний предел интеграла равен нулю. Эта функция является нечетной: Ф0 - z -Ф0 z и связана с функцией Ф z соотношением:

Фz 21 Ф0 z .

Внекоторых учебниках приводятся таблицы значений функции

t 2

- 2 dt 2Ф

z .

2π 0

В практических приложениях теории вероятностей часто требуется

найти вероятность того, что

случайная величина

X~N(a,σ)

примет

значение из заданного интервала x1; x2 :

P x

X x

F x

- F x

Ф(

x2 - a

) - Ф(

x1 - a

) Ф (

x2 - a

)

- (Ф (

x1 - a

)

)) Ф (

x2 - a

) - Ф (

x1 - a

) .

Правило «трѐх сигм»: Теоретически нормальная плотность вероятности отлична от нуля в любой, даже очень отдаленной от a точке x, однако практически почти вся вероятность сосредоточена на отрезке a 3σ (отсюда и название).

Нормальное распределение является симметричным распределением. Однако на практике часто встречаются распределения несимметричные (например, биномиальное распределение при p=0,7).

Коэффициентом асимметрии распределения называется отношение центрального момента третьего порядка к кубу стандартного

отклонения: As μ3 .

σ 3

Для симметричных распределений μ3 0 , поэтому As 0 . Если

As 0, то это говорит о большем влиянии на величину μ3

отрицательных отклонений. В этом случае кривая распределения более

118

полога слева	от M X	и более крутая справа. Если				As 0, то
преобладает	влияние	положительных			отклонений:	кривая
распределения более полога справа и круче слева.
Для нормального распределения			μ4	3,	поэтому эту величину

			σ 4

используют для характеристики меры сглаженности кривой распределения (вблизи центра распределения) по отношению к нормальной кривой.

Коэффициентом эксцесса называется величина: Ex μ4 - 3 .

σ 4

Если для данного распределения Ex 0, то соответствующая кривая распределения более островершинна по сравнению с нормальной кривой. Распределения с E x 0 имеют более плосковершинные кривые по сравнению с нормальным.

Пример 4.1 Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты. Найти среднее время ожидания и среднеквадратическое отклонение случайной величины X – времени ожидания поезда.

Решение: Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0; 2] имеет равномерный закон

распределения p x c	1	1	1	.
	b - a	2 - 0	2

Поэтому вероятность того, что пассажиру придется ждать не более

полминуты, равна: P X 0,5	0,5	1	dx	1		0,5	1	0,25 .
					x

		2		2		0	4
	0

119

Среднее время ожидания:			M X			a b			0	2	1	(мин.),
Среднее время ожидания:			M X						2		1	(мин.),
							2		2
стандартное отклонение: σ X	b -	a	2 - 0		1			0,58 (мин.).


2		3	2	3	3

■

Пример 4.2 Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найдите: а) функцию плотности вероятности и функцию распределения; б) вероятность того, что в течение 100 часов прибор не выйдет из строя.

Решение: а) Среднее время работы прибора – это математическое ожидание случайной величины X – времени работы прибора. По

условию: M X 80 . Для показательного распределения M X λ1 =>

параметр показательного распределения равен λ 801

Тогда функция плотности имеет вид:

	0		при		x 0
p x		1	-	1	x

λe- λx			e	80	при x	0
	80

Функция распределения для x 0			равна F x 0 ,			а при x 0 имеет

вид: F x 1- e- λx 1- e- 80 .

б) Вероятность того, что в течение 100 часов прибор не выйдет из строя:

P X 100 1- P 0 X 100 1- F 100 - F 0 1- ((1 - e-100/80 ) - - (1 - e0 )) e5 / 4 0,286 .

■

Пример 4.3 В некоторой совокупности мужчин средний рост 175 см и стандартное отклонение 10 см. Какая доля мужчин носит одежду II роста

(167-173), III роста (173-179) и IV роста (179-185)?

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2412 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.04.2015204.29 Кб5RP_TOSIO_k1_bak_PIE_elektr.doc
#
19.04.201592.33 Кб119russdolgi.docx
#
21.04.2019114.18 Кб23RUSSKY.DOC
#
30.11.2018147.97 Кб17russky.doc
#
19.04.201549.37 Кб29Russky_yazyk.docx
#
23.03.20165.58 Mб113Rybleva_teoria veroatnosti_2014.pdf
#
27.09.20191.81 Mб12S.Solovejhik_pedagogika_dlq_vseh.doc
#
09.11.2019234.5 Кб4samostoyatelnaya_rabota_Ekonomisty.doc
#
18.04.2015585.22 Кб365sanitaria_i_gigiena_na_predpriatiakh_otrasli.doc
#
18.04.201547.62 Кб15SEMINARY.doc
#
18.04.201568.61 Кб19Seminary_KPRF.doc