
Rybleva_teoria veroatnosti_2014
.pdf
Случайная величина Y имеет биномиальный закон распределения с параметрами n=2, p=0,7. Составьте закон распределения их суммы и найдите еѐ среднее ожидаемое значение.
2.10 Случайная величина X распределена равномерно на множестве {1, 5, 7} с вероятностью p=1/3, а случайная величина Y имеет геометрическое распределение с параметрами n=3, p=0,7. Найдите математическое ожидание и стандартное отклонение случайной
величины Z 2X - 13 Y 5 .
2.11 Экзаменатор задает студенту вопросы, пока тот правильно отвечает. Как только число правильных ответов достигнет четырех, либо студент ответит неправильно, экзаменатор прекращает задавать вопросы. Вероятность правильного ответа на один вопрос равна 2/3. Составьте ряд распределения числа заданных студенту вопросов, вычислите M(X).
Ответы:
2.1распределение равномерное, M(X)=5,5. 2.2 распределение
геометрическое, n=4, M(X)=15/8, D(X)=71/64. 2.3 |
распределение |
||||
биномиальное, M(X)=0,5 (тыс. руб.), σ(X)=0,67 (тыс. руб.). |
2.4 расп- |
||||
ределение |
биномиальное. |
2.5 |
распределение |
Пуассона, |
|
P(X≤5)=0,91608. 2.6 M(X)=4,5; |
σ(X)=0,67. |
2.7 а) 5,5 руб.; |
|
||
б) доход=1,2·затраты => 10a=1,2·255000 => a=30,6 руб. 2.8 а) 2,8; |
|||||
б) 0,4. 2.9 |
M(X+Y)=11,4. 2.11 M(X)=65/27. |
|
|
|
|
101
2.3. Непрерывные случайные величины: способы задания, числовые характеристики и их свойства
Множество значений непрерывной случайной величины представляет собой некоторый промежуток: конечный или бесконечный, т.е. является несчетным множеством. Для непрерывной случайной величины X реальный смысл имеет только такое событие, как попадание в интервал, а не попадание в отдельную точку. Поэтому закон распределения вероятностей величины X должен позволять находить вероятности P x1 X x2 попадания ее значений в любой интервал (x1, x2 ) .
Случайная величина X называется абсолютно непрерывной (далее для краткости будем называть их просто непрерывными), если существует такая функция p x 0 , что для любого возможного
значения случайной величины ее функция распределения может быть
представлена в виде: F x |
x |
p x dx . |
-
Функция p x называется плотностью распределения
вероятностей и определяет закон распределения для непрерывной случайной величины. График функции плотности распределения называется кривой распределения.
Свойства плотности распределения:
1)Вероятность попадания непрерывной случайной величины в интервал равна определенному интегралу от ее плотности:
P x1 X x2 x2 p x dx .
x1
2)Суммарная площадь под кривой распределения равна единице:
p x dx 1.
-
102
3)В точках непрерывности: p x F (x) .
4)P X x 0 .
Следствие. Для непрерывной случайной величины X:
P x1 X x2 P x1 X x2 P x1 X x2 P x1 X x2 .
Понятие математического ожидания M X и дисперсии D X ,
определенные для дискретной случайной величины, можно распространить на непрерывные случайные величины.
Для получения формул математического ожидания и дисперсии
непрерывной случайной |
величины |
достаточно в |
соответствующих |
||||
формулах для |
дискретной |
случайной величины |
X заменить знак |
||||
|
|
|
|
|
|
|
|
суммирования |
по |
всем |
ее |
значениям знаком |
интеграла с |
||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бесконечными пределами |
|
, |
«скачущий» элемент |
xi |
- непрерывно |
||
|
|
- |
|
|
|
|
|
меняющимся x, а вероятность pi - элементом вероятности p x dx .
В результате получим следующие формулы:
M X |
|
xp x dx , если интеграл абсолютно сходится, |
|
|||
|
|
|||||
|
- |
|
|
|
|
|
D X |
|
(x - M X )2 p x dx |
или D X |
|
x 2p x dx - M2 |
X . |
|
|
|||||
|
- |
|
|
- |
|
|
Все свойства математического ожидания и дисперсии, рассмотренные выше для дискретных случайных величин, справедливы и для непрерывных случайных величин.
Начальным моментом k-го порядка, который обозначается как
γk , называется математическое ожидание k-ой степени случайной величины: γk M X k .
103
Например, первый начальный момент – это математическое ожидание: γ1 M X , а дисперсия равна D X γ2 - γ12 .
Центральным моментом k-го порядка, который обозначается как μk , называется математическое ожидание k-ой степени отклонения
случайной |
величины |
от |
своего математического |
ожидания: |
μk |
||||
M X M X k . |
|
|
|
|
|
|
|||
|
|
Например, второй центральный момент – это дисперсия: |
|
||||||
|
|
μ M X M X 2 M X 2 M2 X D X |
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
Любой центральный момент можно выразить через начальный. |
|||||||
Например, третий центральный момент: |
|
|
|
|
|||||
μ M X - M X 3 M X - γ 3 M X 3 - 3γ X 2 |
3γ2 X - γ 3 |
|
|||||||
3 |
|
|
|
|
1 |
1 |
1 |
1 |
|
γ |
3 |
- 3γ γ |
2γ3 . |
|
|
|
|
|
|
|
1 2 |
1 |
|
|
|
|
|
|
|
|
|
Точка локального максимума функции плотности вероятности p x |
|||||||
называется модой. |
|
|
|
|
|
|
|||
|
|
Мода случайной величины X обозначается Mo X . Для дискретной |
|||||||
случайной |
величины |
X |
модой является |
возможное |
значение |
xi , |
|||
которому соответствует наибольшая вероятность pi . Распределения,
имеющие одну моду, называются одномодальными. Встречаются и многомодальные распределения.
Функция распределения случайной величины X любой точке x p
ставит в соответствие вероятность p F xp P X xp . Иногда
возникает обратная задача: по заданному значению p найти такое x p ,
чтобы F xp p . Такая точка x p называется квантилью уровня p .
Квантиль уровня p 1/2 называется медианой распределения.
Медиана случайной величины X обозначается Me X . Для непрерывных случайных величин медиана – это граница, которая делит
104
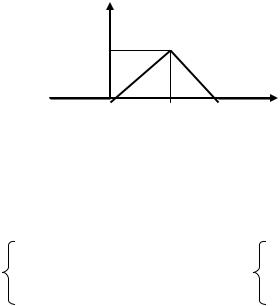
площадь криволинейной трапеции под кривой распределения на две равные части.
Пример 3.1 Кривая распределения случайной величины X на отрез-
ке [ 0; 4 ] имеет вид равнобедренного треугольника, вне этого отрезка p x 0. Найдите для данной случайной величины: а) функцию плотности распределения p x ; б) математическое ожидание и стандартное отклонение; в) функцию распределения F x ; г) ве-
роятности событий P X 1 , P 1 X 3 и P X 3 ; д) моду, медиану и квантили x0,1 , x0,9 .
Решение: а) Сначала найдем высоту равнобедренного треугольника h. По свойству 2 функции плотности площадь криволинейной трапеции (в
данном |
случае |
треугольника) должна |
быть равна единице: |
|||||||
S |
1 |
ah |
(4 - 0)h |
|
4 |
h 2h 1. Отсюда h |
1 |
. |
||
2 |
2 |
2 |
2 |
|||||||
|
|
|
|
|
|
|||||
p x h
0 2 4 x Рис. 8
Так как распределение симметрично относительно прямой x 2 и на каждом из отрезков [ 0; 2] и [ 2; 4] функция плотности распределения представляет собой прямые p1 x kx b и p2 x cx d , то имеем:
|
|
p1 0 b 0 |
p2 2 4c d 0 |
|
|
|
||||||||
|
p 2 2k b |
1 |
и |
p 4 |
2c d |
1 |
|
|
Отсюда получим: |
|||||
|
|
|
|
|
|
|
||||||||
|
1 |
2 |
|
2 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
p |
x |
|
x |
- плотность на отрезке [ 0; |
2] и |
p x |
- |
x |
1 - плотность на |
|||||
|
|
|||||||||||||
1 |
4 |
|
|
|
|
|
2 |
|
|
4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
отрезке [ 2; 4]. |
|
|
|
|
|
|
|
|
||||||
б) |
Найдем математическое ожидание: |
|
|
|
|
|
|
|||||||
105

M X |
|
xp x dx 0 |
2 |
|
|
|
|
|
x dx |
4 |
|
|
|
|
x dx 0 |
2 |
|
x |
|
||||||||||||
|
|
|
|
|
xp |
|
|
|
xp |
|
|
x |
dx |
||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
4 |
|
|||||||
|
|
- |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4 |
|
|
x |
|
x 3 |
|
2 |
|
x 2 |
|
4 |
|
x 3 |
|
4 |
|
|
12 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x(1- |
|
)dx |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
6 - |
|
|
2 . |
|
|
|
|
||||
4 |
12 |
|
|
|
2 |
|
|
|
12 |
|
|
|
3 |
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Этот же результат можно было получить иначе: достаточно посмотреть на график функции плотности распределения – понятно, что среднее значение лежит посередине (в силу симметрии кривой) отрезка
[ 0; 4], т.е. |
равно |
0 4 |
2 . |
Для нахождения стандартного отклонения |
||||||||||||||||||||
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сначала |
вычислим |
второй |
|
|
|
|
|
начальный |
момент |
γ2 |
||||||||||||||
M X 2 2 x2 |
x |
dx 4 |
x2(1- |
x |
)dx |
14 |
. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
4 |
|
2 |
|
4 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда дисперсия равна: |
|
D(X) γ |
|
|
X - γ 2 |
X |
14 |
|
- 4 |
2 |
. |
|
||||||||||||
|
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Стандартное отклонение: σ X |
|
|
|
|
|
|
|
|
||||||||||||||||
D X |
2 / 3 |
0,817 . |
|
|
|
|
||||||||||||||||||
в) Функция |
распределения |
|
для |
|
непрерывной случайной величины |
|||||||||||||||||||
x
определяется по функции плотности: F x p t dt . Найдем ее для
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
каждого интервала в отдельности: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
если x 0 , то p x 0 , следовательно F x |
x |
|
|
|
|||||||||||||||||
|
|
0dt 0 ; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
если 0 x 2 , то p x |
|
x |
. |
|
=> |
F x 0 x |
t |
dt |
x2 |
; |
|||||||||||
4 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
4 |
|
8 |
|
|||||
|
если 2 x 4 , то p x 1- |
x |
. |
=> |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
t |
x |
t |
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
F x 0 |
dt (1- |
)dt 0 - |
|
|
x - 1 ; |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
4 |
2 |
4 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
t |
|
|
4 |
|
|
|
t |
|
|
|
|
|
|
|
|
если x ≥ 4 , то F x 0 |
|
|
dt (1- |
|
)dt 0 1. |
|
|||||||||||||||
4 |
|
|
4 |
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
106
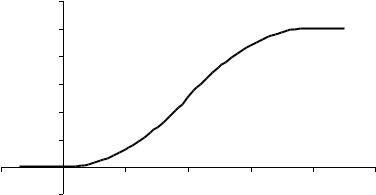
Построим график функции распределения: |
|
|
|||||||
F(x) |
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
х |
|
-1 |
-0,2 |
0 |
1 |
2 |
3 |
4 |
5 |
||
|
|||||||||
Рис. 9
г) |
P X 1 F 1 |
x2 |
|
|
1 |
0,125 ; |
|
|
|||||
|
8 |
|
x 1 |
8 |
|
|
|
|
|
|
|
|
|
|
P 1 X 3 F 3 - F 1 0,75 ; |
|||||
|
P X 3 1- P X 3 1- F 3 1- 7/8 1/8 0,125 , |
|||||
т.е. вероятности событий P X 1 P X 3 - в силу симметрии кривой |
||||||
распределения. |
|
|
|
|
||
д) |
Мода и медиана данной случайной величины совпадают и равны |
|||||
математическому ожиданию: M X Mo X Me X 2 . |
||||||
Квантиль уровня 0,1 |
|
удовлетворяет условию:F x0,1 0,1. Такое |
||||
значение функция распределения принимает на отрезке [ 0; 2], где она
задается как |
x 2 |
. Получаем уравнение: |
x 2 |
0,1. Отсюда x0,1 |
0,894 . |
|
8 |
8 |
|||||
|
|
|
|
Квантиль уровня 0,9 в силу симметричности распределения находится на таком же расстоянии от правой точки x 4 , на каком расстоянии находится квантиль уровня 0,1 от левой точки x 0 , значит получим: x0,9 4 - 0,894 3,106 .
■
Пример 3.2 Какие из перечисленных функций могут быть функциями плотности распределения вероятности?
107

а) p x |
4 при |
0 x 0,25 ; |
|
0 |
иначе |
б) p x |
0,5·sin x |
при - π/2 x π/2 |
|
0 иначе |
|
|
|
Решение: Для того чтобы выяснить, может ли данная функция являться функцией плотности, необходимо проверить удовлетворяет ли
рассматриваемая функция условиям: p x 0 и |
|
p x dx 1. |
|
||
|
- |
|
а) Данная функция на всей области определения неотрицательна и площадь криволинейной трапеции (в данном случае прямоугольника) равна 4·0,25=1. Значит, данная функция является плотностью.
б) На интервалах (-π/2; 0) и (0; π/2) функция имеет разные знаки и поэтому не может быть плотностью.
■
Пример 3.3 Задана функция распределения случайной величины X:
|
0 |
при |
x -π/4 |
F x |
a·sin(x - π/4) 1/2 |
при -π/4 ≤ x 3π/4 |
|
|
1 |
при |
x ≥ 3π/4 |
Найдите: а) плотность распределения p x ; б) коэффициент a;
в) вероятность попадания значения случайной величины X в интервал
( π/4; 3π/4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: а) |
По свойству 3 для функции плотности получим: |
|||||||||||||||||
|
|
|
0 |
при |
x -π/4 |
|
|
|
|
|
|
|||||||
|
|
x |
|
π |
|
|
π |
|
3π |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a·cos( x - 4 ) при |
- 4 |
|
≤ x 4 |
|
|
|
|
|
|
||||||||
p x F |
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
при |
x ≥ 3π / 4 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
По свойству 2 функции плотности имеем: |
p x dx 1, значит: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
3π/4 |
|
|
|
|
|
3π / 4 |
|
|
π |
|
π |
|
||||||
|
a·cos(x - π/4)dx a·sin(x - π/4) |
a·(sin |
- sin(- |
)) 2a 1. |
||||||||||||||
-π/4 |
|
2 |
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
-π/4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
108 |
|
|
|
|
|
|
|
|
|
|||
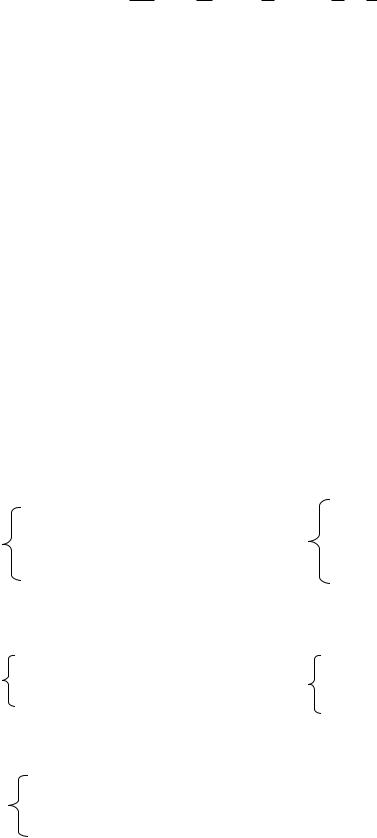
Отсюда a 1/ 2.
в) Вероятность попадания значения случайной величины в заданный интервал (по свойству 2 функции распределения) равна:
P π/4 X 3π/4 F(34π ) - F( π4 ) 1- 21 sin 0 - 21 21 .
■
Задачи для самостоятельного решения:
3.1Кривая распределения случайной величины X на отрезке
[ 0; 4] имеет вид перевернутого равнобедренного треугольника, вне этого отрезка p x 0 . Найдите для данной случайной величины:
а) |
функцию плотности распределения p x ; |
|
б) |
математическое ожидание и стандартное отклонение; |
|
в) функцию распределения F x ; |
|
|
г) |
вероятности событий P X 1 , |
P 1 X 3 и P X 3 ; |
д) |
моду, медиану и квантили x0,1 , |
x0,9 . |
3.2 Какие из перечисленных ниже функций являются функциями распределения:
|
F x |
|
|
0 при |
x 0 |
|
F x |
|
|
0 при |
x 0 |
|
а) |
|
|
x при |
0 x 1 |
б) |
|
x 2 при |
0 x 1 |
||||
|
|
|
|
1 при |
x 1 |
|
|
|
|
1 при |
x 1 |
|
в) |
F x |
π |
arctg x ; |
г) |
F x |
1 |
|
1 |
arctgx ; |
|||
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
2 |
|
π |
|
||
д) |
F x |
|
|
0 при |
x 0 |
е) |
F x |
|
0 |
при |
x 0 |
|
|
|
1 при |
x 0 |
|
1 при x 0 |
|||||||
|
|
|
|
|
|
|
||||||
3.3 |
Какие из перечисленных ниже функций являются функциями |
||||
плотности распределения вероятностей: |
|
|
|
||
а) |
p x |
0 при x 0 или x 1 |
б) p x |
x |
; |
1 при 0 x 1 |
|
||||
1 x 2 |
|||||
109

0 при |
x 0 |
0 при |
x 0 |
|
в) p x sin x |
при |
0 x π |
г) p x x(1 - x) при |
0 x 1 |
0 |
при |
x π |
0 при |
x 1 |
Для тех функций, которые являются плотностью, найдите соответствующую функцию распределения.
3.4 Функция распределения годового дохода лица, облагаемого налогом, имеет вид (распределение Парето):
|
x |
0 |
a |
||
F x |
1- |
|
|
||
x |
|||||
|
|
|
|||
|
|
0 |
|
при |
|
при
x
xx0 .
x0
Для |
a 4 и x0 |
80 тыс. руб. найдите средний ожидаемый доход и |
|||
доход, гарантированный на 90%. |
|
|
|||
3.5 |
Случайная |
величина X имеет плотность p x |
|
c |
(закон |
|
|
||||
|
x 2 |
||||
|
|
1 |
|
||
Коши). Найдите: а) коэффициент c и функцию распределения F x ; б)
вероятность P X 1 ; в) математическое ожидание, моду и медиану данной случайной величины.
3.6 |
Случайная величина X при x 0 характеризуется |
функцией |
||
|
- |
x 2 |
|
|
|
|
|
|
|
распределения F x 1- e 2σ 2 |
(распределение Рэлея). |
Найдите |
||
плотность p x .
3.7Случайная величина X задана плотностью вероятности
|
p x |
1 |
|
|
|
||
(распределение Лапласа) |
·e- |
|
x |
|
. Найдите математическое |
||
2 |
|
|
|||||
|
|
|
|
|
|
|
|
ожидание величины X. |
|
|
|
|
|
|
|
Ответы:
3.1 p(x)=-x/4+1/2 при 0≤x≤2, p(x)=x/4-1/2 при 2<x≤4, M(X)=2.
110
