Метод Ньютона
Метод Ньютона применяется к решению уравнения, когда функция является непрерывно дифференцируемой функцией. Также вначале отделим корень уравнения на отрезке .
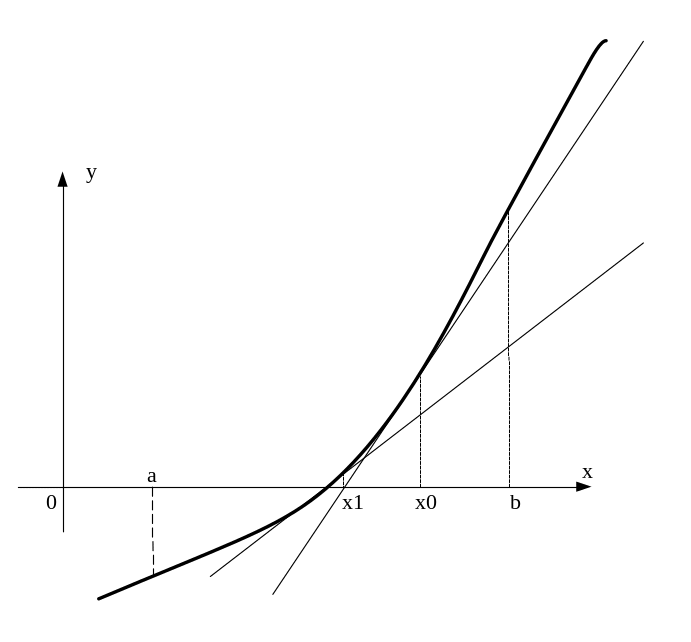
Рис. 5
Для начала вычислений
требуется задание одного начального
приближения
внутри отрезка
.
Первое приближение вычисляется через
это начальное по формуле рис. 5:
Общая формула метода Ньютона может быть записана с помощью рекуррентного соотношения:
,
где
и
.
Каждое последующее
приближение вычисляется через предыдущее.
Геометрически точка
является значением абсциссы точки
пересечения касательной к кривой
в точке
с осью абсцисс, поэтому часто метод
Ньютона называют также методом
касательных.
На практике можно
встреться со случаем сходимости метода
Ньютона, когда
далеко от искомого корня, так и со случаем
расходимости метода для
-
близких к корню. Возможен также случай
зацикливания метода. Часто при неудачном
выборе начального приближения
нет монотонного убывания последовательности
.
В таком случае вычисления можно проводить
по модифицированному методу Ньютона:
а сомножители
выбираются так, чтобы выполнялось
неравенство
.
Сомножители
сжимают отображение. Рекомендуется
всегда выбирать достаточно тесные
границы корня
,
и в качестве начального приближения
выбирать такую точку отрезка
,
где знаки функции
и ее кривизны
совпадают.
Условием выхода
из итерационного процесса по методу
Ньютона является выполнение неравенства
Пример: уточнить корень уравнения , находящийся на методом Ньютона с точностью .
Выберем в качестве
начального приближения
середину отрезка
,
т.е.
,
1. По рекуррентной формуле метода Ньютона вычислим
вычисления по
методу Ньютона следует продолжить.
2. По рекуррентной формуле метода Ньютона вычислим
вычисления по
методу Ньютона можно закончить.
Метод простой итерации
Метод простой
итерации применяется к решению уравнения
с выделенным значением неизвестного в
правой части
и состоит в построении последовательности
,
начиная с некоторого начального значения
по правилу
Если
непрерывная функция, а
-
сходящаяся последовательность, то
значение
является корнем уравнения.
Условием сходимости процесса итераций, т.е. условие существования предела есть соблюдение неравенства, носящего название принципа сжатых отображений:
,
где
для всех
в интервале отделения корня. Сходимость
будет тем более быстрой, чем меньше
величина
.
Погрешности метода на
и
связаны неравенством
,
что позволяет отнести метод простой итерации к классу методов с линейной скоростью сходимости. Во всех итерационных методах уточнения корней уравнений в качестве критерия окончания процесса вычислений выбрано условие:
.
При этом предполагается, что чем больше проделано уточнений, тем выше точность определения корня.
Метод простой итерации имеет линейную скорость сходимости, чтобы увеличить скорость сходимости следует выбирать достаточно близкие значения интервала отделения корня , что при высокой скорости вычислений современных ПК не представляет больших затруднений.
Следует четко уяснить, что во всех итерационных методах есть условие входа в итерационный процесс и условие выхода из итерационного процесса, в противном случае он может продолжаться бесконечно, бесконечно близко можно приближаться к точному решению, но в общем случае точное решение не достижимо.
Пример: уточнить
корень уравнения
,
находящийся на
методом простой итерации с точностью
.
Преобразуем
заданное уравнение применительно к
методу простой итерации. Оставим
слагаемое
в левой части уравнения, остальные
слагаемые перенесем в правую часть с
противоположными знаками.
Проверяем принцип сжатых отображений для выбранной нами итерирующей функции (рассматриваем один из множества возможных способов представления итерирующей функции).
Проанализируем,
как ведет себя функция
на отрезке
.
Построим таблицу
x |
-1 |
-0,9 |
-0,8 |
-0,7 |
-0,6 |
-0,5 |
-0,4 |
-0,3 |
-0,2 |
-0,1 |
0 |
|
1,818 |
1,587 |
1,367 |
1,158 |
0,96 |
0,773 |
0,596 |
0,431 |
0,276 |
0,133 |
0 |
Из таблицы видно,
что концы отрезка, на котором выполняется
условие
,
соответственно равны
.
Таким образом
будем уточнять корень на отрезке
с помощью следующего рекуррентного
уравнения
.
Выберем в качестве
начального приближения
Сведем расчеты в таблицу
Таблица 5
№ |
|
|
|
1 |
-0,6 |
-0,45891 |
-0,766 |
2 |
-0,45891 |
-0,57568 |
0,642255 |
3 |
-0,57568 |
-0,48169 |
-0,51695 |
4 |
-0,48169 |
-0,5593 |
0,4268 |
5 |
-0,5593 |
-0,4964 |
-0,34597 |
6 |
-0,4964 |
-0,54822 |
0,285 |
7 |
-0,54822 |
-0,50606 |
-0,23188 |
8 |
-0,50606 |
-0,54074 |
0,19073 |
9 |
-0,54074 |
-0,51245 |
-0,15558 |
10 |
-0,51245 |
-0,53569 |
0,1278 |
11 |
-0,53569 |
-0,51671 |
-0,1044 |
12 |
-0,51671 |
-0,53229 |
0,0857 |
13 |
-0,53229 |
-0,51962 |
-0,069 |
14 |
-0,51962 |
-0,52994 |
0,057 |
15 |
-0,52994 |
-0,5215 |
-0,046 |
На 15 шаге выполняется
условие выхода из итерационного процесса
.
Отсюда следует, что корень уравнения
найденный по методу простой итерации
с точностью
равен
.