Мат_методы в горном деле

МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ГОРНОМ МЕНЕДЖМЕНТЕ

Иркутск

2011

Министерство образования и науки Российской федерации Федеральное агентство по образованию

Иркутский государственный технический университет

М.И. Щадов, И.А. Огнѐв, В.Ю. Конюхов

МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ГОРНОМ МЕНЕДЖМЕНТЕ

Допущено учебно-методическим объединением вузов Российской Федерации по образованию в области горного дела в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки «Горное дело» и по специальности «Менеджмент организации» (специализация «Производственный менеджмент в горном деле») направления подготовки «Менеджмент».

Издательство Иркутского государственного технического университета

2011

1

УДК 517.977.5+519.85 ББК 22.16

Рецензенты: д-р эконом. наук, профессор кафедры «Экономика предприятий и предпринимательской деятельности» Байкальского государственного университета экономики и права Т.В. Светник, д-р эконом. наук, вице-президент Торгово-промышленной

палаты Восточной Сибири, профессор Р.Ф. Старков

Щадов М.И., Огнѐв И.А., Конюхов В.Ю. Математические модели в горном менеджменте: учебное пособие.– Иркутск: Изд-во ИрГТУ, 2011 - 64 с.

В пособии рассмотрены применение методов линейного программирования к решению различных задач планирования и управления горным производством. Подробно показано решение этих задач аналитически и с помощью табличного процессора Excel. Предложены варианты заданий для самостоятельной и аудиторной работы.

Предназначено для студентов инженерных и экономических специальностей вузов и преподавателей высшей математики.

Печатается по решению редакционно-издательского совета Иркутского государственного университета.

ISBN 978-5-8038-0484-0 © М.И. Щадов, И.А. Огнѐв, В.Ю. Конюхов, 2011

©Оригинал-макет: И.А. Огнѐв, 2011

©Иркутский государственный технический университет, 2011

2

3

Введение

Современная горная промышленность характеризуется огромными масштабами производства, большими производственными затратами на добычу и переработку полезных ископаемых и имеет высокую народнохозяйственную значимость.

Управление предприятиями горной отрасли предполагает строгий учет и контроль расходования и экономии природных, материальных и финансовых ресурсов с применением современных методов количественного анализа, с широким использованием компьютерной техники. Это в значительной степени позволяет повысить эффективность, качество и действенность плановых и управленческих решений.

Математические методы являются эффективным инструментом анализа хозяйственных ситуаций, позволяют выбирать оптимальные варианты развития

иразмещения производства. Использование экономико-математических моделей помогает принимать оптимальные решения при разработке планов и в процессе их реализации, определять наиболее эффективные варианты реконструкций и расширения действующих предприятий, находить оптимальное сочетание трудовых и материальных затрат и т. д.

Особенностью процессов менеджмента на горных предприятиях в общем случае является необходимость принятия решений при огромном многообразии производственных ситуаций. В связи с этим необходимо уметь количественно оценивать степень осуществления поставленной цели при каждом варианте решения.

Принятие решений при планировании и управлении горным производством, как правило, требует привлечения специального математического аппарата. Математические методы условно делят на два класса: вероятностные и детерминированные. К вероятностным методам относятся регрессионный анализ, различные методы прогнозирования, теория игр, теория принятия решений, имитационное моделирование и др.; к детерминированным - матричные методы, линейное и нелинейное программирование, потоки в сетях, и др.

Практическое использование математических моделей реальной размерности, как правило, требует решения задач на компьютере. Традиционная математическая подготовка специалиста была ориентирована на проведение расчетов вручную, что требовало больших затрат времени. Но теперь, в связи с переходом на двухуровневую систему образования, необходимо научить студентов решать задачи оптимизации более эффективно и с меньшими затратами времени. Такую возможность дают не только специализированные мате-

матические программы, такие как MatLab, Mathcad, Maple, Stastistica и др., но

ипрограммы общего назначения, такие как Excel, Calc и др.

Освоение специальных программ - достаточно трудоемкая задача. Тем более что фактически все они нерусифицированы. В то же время табличный процессор Excel намного легче в освоении, и его современная версия позволяет решать большое количество оптимизационных математических задач.

4

Глава 1. Методы математического программирования

Формальная постановка задачи

При формальной постановке задачи математического программирования основными понятиями являются инструментальные переменные, допустимое множество и целевая функция.

Задача заключается в нахождении значений переменных x1,...,xn, которые называются инструментальными.

xn

Вектор x , записанный в виде вектора-столбца или вектора-строки, есть вектор инструментальных переменных в n-мерном евклидовом пространстве Еn.

Если вектор инструментальных переменных x удовлетворяет ограничениям задачи, он называется допустимым, а множество всех допустимых векторов образует допустимое множество X, где X En . Так как задача заключается

в выборе вектора инструментальных переменных из допустимого множества X , то в любой нетривиальной задаче оно является непустым.

Целевая функция - это краткое математическое представление цели данной задачи. Обычно это действительная непрерывно дифференцируемая функция вектора инструментальных переменных.

Общая задача математического программирования состоит в выборе вектора инструментальных переменных из множества возможностей, максимизирующего значение целевой функции:

F(x) max, x X .

При этом учитывается, что задача максимизации функции эквивалентна задаче минимизации функции F(x) при тех же условиях.

Классификация задач математического программирования

Задачи математического программирования можно разделить на группы в зависимости от характера целевой функции и типа ограничений, накладываемых на переменные. Метод поиска экстремума функции одной или нескольких переменных из области допустимых значений выбирают исходя из стратегии оптимизации.

Для задач математического программирования конечный алгоритм решения должен обеспечивать отыскание глобального оптимума или указывать на его отсутствие за конечное число шагов. Из-за большой размерности реальных задач преобладают стратегии последовательного поиска – как единственно возможный путь достижения результата.

5

Таблица 1.1. Классификация задач математического программирования

Приведенная группировка задач и методов [11] весьма условна, так как многие задачи могут быть отнесены к нескольким группам и решаться разными методами.

Принято выделять три основных вида общей задачи математического программирования: каноническая задача математического программирования, задача нелинейного программирования и задача линейного программирования.

Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно-линейного программирования.

В канонической задаче математического программирования все ограни-

чения представляют собой равенства

ные действительные числа, называемые константами ограничений.

6

Таким образом, задача линейного программирования заключается в нахождении неотрицательных значений переменных, удовлетворяющих ограничениям (1.6), (1.7) и максимизирующих заданную линейную форму(1.5):

F(x) max, при Ах b, x 0 .

Отсюда видно, что задача линейного программирования является частным случаем задачи нелинейного программирования, в которой целевая функция и функции ограничений линейны.

Глава 2. Решение задач менеджмента горного производства методами линейного программирования в Excel

В настоящее время накоплен значительный опыт применения моделей линейного программирования в горном производстве. К числу решаемых с его помощью задач можно отнести планирование распределения добычи по отдельным участкам горного предприятия, распределение капиталовложений между различными действующими или проектируемыми предприятиями, составление оптимального плана перевозок, определение оптимальной загрузки оборудования и транспорта и т.д.

Во многих случаях решения, полученные с помощью линейного программирования, дают ощутимый экономический эффект.

Рассмотрим решения нескольких типовых задач оптимизации горного производства методами линейного программирования и проанализируем их.

Планирование добычи руды заданного состава

Требуется составить план эксплуатации карьера при условии, что суммарные затраты на транспортирование руды в рассматриваемом периоде времени не должны превышать 8690 руб., а содержание Р2О5 должно быть в пределах 6,8 - 7,0 %. План должен обеспечивать максимально возможную добычу руды. Данные по участкам карьера приведены в табл. 2.1.

Обозначим через xi искомый объем добычи на i-м участке, тыс. т. Запишем математическую модель задачи. Целевая функция — суммарный объем добычи руды.

Ограничения:

а) по величине затрат на транспорт

;

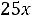
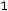
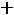
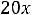
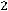
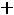
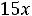
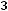
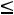
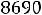б) по качеству руды

8

;

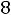
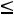
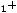
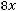
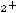
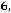
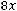
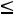
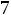
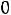в) по максимально допустимой добыче участков

;

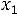
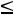
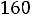
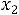
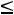
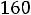
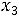
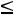
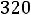г) по неотрицательности объемов добычи

.

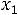
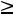
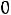
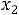
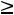
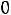
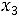
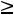
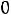После очевидных преобразований ограничение «б» запишем в виде двух неравенств:

;

.

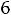
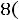
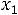
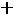
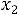
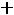
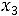
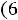
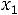
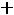
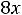
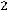
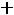
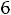
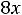
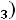
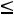
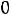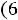
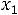
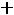
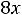
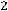
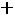
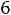
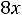
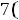
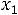
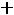
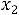
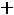
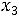
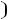
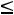
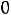Теперь можно приступать к решению задачи на компьютере.

1.Создадим новую рабочую книгу (Office→Создать→Новая книга).

2.На листе 1 в ячейки F3:F5 занесем правые части неравенств - числа 8690, 0 и 0 соответственно.

3.В ячейки A2:C2 занесем начальные значения неизвестных 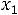, 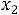и 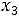(нули) — в дальнейшем значения этих ячеек будут подобраны автоматически.

4.В ячейках диапазона A3: C5 разместим коэффициенты при неизвестных из левых частей ограничений.

5.В ячейках D3:D5 укажем формулы для расчета левых частей неравенств. В ячейке D3 формула будет иметь вид =СУММПРОИЗВ($A$2:$C$2;A3:C3),

аостальные формулы можно получить методом автозаполнения. В ячейку Е4 занесем формулу для расчета первого (левого) ограничения по качеству руды. В ячейку Е5 - формулу для расчета второго (правого) ограничения.

6.В ячейки А6:С6 занесем ограничения по максимально допустимой добыче участков.

7.В ячейку F2 занесем формулу целевой функции =СУММ(A2:C2). Резуль-

тат ввода данных в рабочую таблицу представлен на рис. 2.1.

Рис.2.1. Результат ввода данных

8. Дадим команду Данные→Поиск решения — откроется диалоговое окно

Поиск решения.

9. В поле Установить целевую ячейку мышью укажем ячейку, содержащую оптимизируемое значение (F2) (рис. 2.2). Установим переключатель Равной в положение максимальному значению (требуется максимальный объем добычи руды).

9