
Мат_методы в горном деле
.pdf
j - индекс продукции ( 
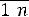 );
);
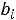 - запас ресурса i-го вида, т. е. максимальное количество этого ресурса, которое может быть израсходовано на производство продукции;
- запас ресурса i-го вида, т. е. максимальное количество этого ресурса, которое может быть израсходовано на производство продукции;
- удельный расход i-го ресурса на продукцию j-го вида, т.е. количество единиц данного ресурса, которое затрачивается на производство одной единицы указанной продукции;
- прибыль, получаемая от одной единицы выпускаемой продукции j-го вида.
Величины т, п, |
, , обычно известны. Обозначим - количество |
|
продукции j-го вида, |
планируемое к выпуску. Величины |
должны быть по- |
добраны так, чтобы обеспечить получение максимальной прибыли, а расход ресурсов не превышал их запаса. Это приводит к следующей математической задаче. Целевая функция - суммарная прибыль.
(3.1)
Ограничения:
а) по запасам ресурсов
. . . . . . . . . . . . . . . . . . . . . |
(3.2) |
|
б) по неотрицательности искомых величин
. . . 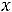
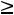
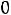
 (3.3)
(3.3)
Поставим теперь задачу найти оценки ресурсов, объективно обусловленные для данного производства. Очевидно, что эти оценки должны находиться из условий рентабельности производства. Это означает, что, вопервых, стоимость всех ресурсов должна быть минимальной и, во-вторых, стоимость всех ресурсов, расходуемых на выпуск единицы продукции, должна быть не ниже получаемой от нее прибыли.
Если обозначить через 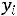 оценку i-го ресурса, то указанные соображения приводят к следующей задаче ЛП. Целевая функция - суммарная стоимость всех ресурсов:
оценку i-го ресурса, то указанные соображения приводят к следующей задаче ЛП. Целевая функция - суммарная стоимость всех ресурсов:
. |
(3.4) |
Ограничения:
а) по стоимости ресурсов, затраченных на выпуск единицы продукции
. . . . . . . . . . . . . . . . . . . . . |
(3.5) |
|
б) по неотрицательности оценок ресурсов
. . . 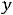
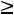
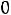
 (3.6)
(3.6)
Задача (3.1) — (3.3) называется двойственной по отношению к задаче (3.4) — (3.6). Отметим следующие особенности двойственной задачи.
20

1.Коэффициентами ее целевой функции служат правые части основных ограничений исходной задачи.
2.Правыми частями в основных ограничениях двойственной задачи служат коэффициенты целевой функции исходной задачи.
3.Матрица коэффициентов при неизвестных в двойственной задаче представляет собой транспонированную матрицу коэффициентов при неизвестных в исходной задаче.
4.В исходной задаче целевая функция максимизируется, а в двойственной - минимизируется, причем в основных ограничениях при максимизации целевой функции будут знаки неравенств «≤», а при минимизации «≥».
5.В обеих задачах присутствуют условия неотрицательности искомых величин.
Из указанных особенностей следует, что основным ограничениям одной из двойственных задач ставятся в соответствие искомые величины другой. Поэтому, например, в первом ограничении двойственной задачи участвуют только
коэффициенты при х1 в исходной задаче, во втором ограничении — только коэффициенты при х2 и т. д. Это облегчает написание двойственной задачи.
Например, для задачи ЛП:
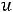
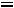
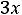
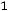
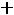
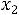
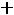
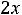
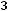
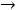
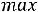 ;
;
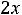
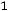

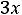
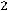
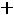
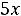
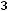
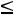
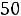 ;
;
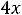
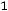
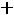
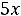
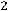
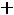
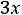
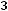
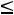
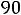 ;
;
двойственной будет задача
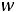

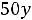
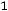
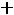
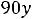
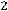
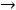
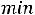 ;
;
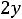
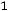
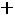
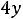
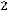
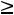
 ;
;
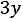
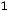
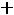
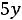
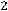
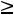
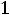 ;
;
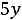
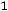
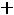
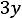
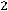
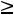
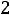 ;
;
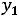
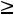

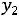
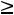
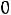 .
.
Симметрия двойственных задач нарушается, если в исходной задаче среди ограничений имеются уравнения или некоторые из неизвестных могут принимать значения любого знака. В этом случае при составлении двойственной задачи руководствуются следующими правилами:
ограничению-равенству исходной задачи в двойственной задаче соответствует переменная любого знака;
переменной любого знака в исходной задаче соответствует ограничениеравенство двойственной задачи.
В остальном действуют те же принципы, что и в симметричном случае. Например, для задачи
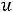
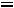
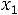
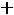
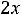
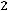
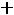
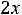
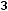
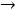
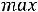 ;
;
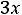
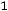
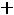
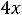
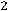
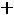
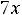
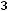
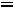
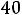 ;
;
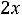
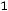
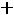
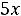
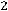
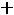
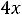
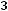
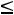
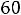 ;
;
двойственной будет задача
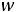
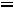
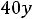
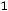
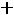
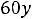
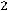
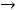
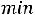 ;
;
21
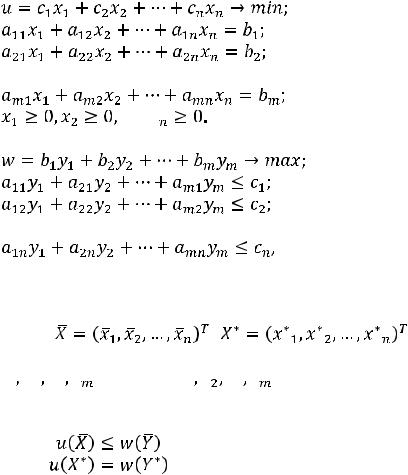
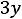
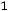
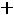
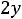
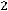

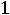 ;
;

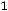
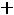
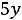
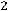
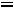
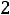 ;
;
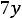
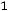
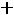
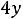
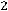
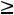
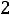 ;
;
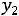
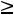
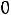 .
.
Здесь во втором ограничении двойственной задачи поставлен знак равенства потому, что в исходной задаче переменная х2 — любого знака, а переменная у1 в двойственной задаче может быть любого знака на том основании, что первое ограничение в исходной задаче является уравнением.
Для канонической задачи ЛП
. . . . . . . . . . . . . . . . . . . . .
. . . 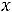
двойственной является задача
. . . . . . . . . . . . . . . . . . . . .
в которой искомые величины могут быть любого знака.
Рассмотрим некоторые важные результаты, известные в теории двойст-
венных задач. |
|
|
Пусть |
, |
обозначают соответст- |
венно допустимый и оптимальный планы исходной задачи на максимум, а 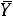
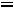
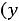
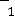


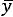
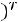 ,
, 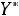

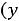
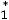


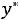
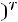 - то же для двойственной задачи на минимум. В теории ЛП доказано, что значения целевых функций двойственных задач для указанных выше планов удовлетворяют условиям:
- то же для двойственной задачи на минимум. В теории ЛП доказано, что значения целевых функций двойственных задач для указанных выше планов удовлетворяют условиям:
, |
(3.7) |
. |
(3.8) |
Вслучае задачи распределения ресурсов это интерпретируется следующим образом. Если оценки ресурсов обеспечивают рентабельность производства, то максимальная прибыль от выпуска продукции равна минимальной суммарной оценке всех ресурсов, если же выпуск продукции спланирован не оптимально или оценки ресурсов не являются оптимальными, то получаемая прибыль ниже суммарной оценки ресурсов.
Это означает, что объективно обусловленные условиями производства
оценки 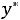 ресурсов, получаемые в результате решения двойственной задачи, можно использовать в качестве стимула оптимального выпуска продукции, обеспечивающего получение максимальной прибыли.
ресурсов, получаемые в результате решения двойственной задачи, можно использовать в качестве стимула оптимального выпуска продукции, обеспечивающего получение максимальной прибыли.
Втеории двойственности доказано, что если одна из двойственных задач имеет оптимальный план, то и другая задача разрешима. Из этого следует, что
22

существование оптимальных оценок ресурсов гарантирует и существование оптимального плана выпуска продукции.
Важную роль играют так называемые соотношения дополняющей нежесткости:
(3.9)
(3.10)
которые можно сформулировать следующим образом. Если оптимальный план удовлетворяет некоторому основному ограничению как строгому неравенству, т.е. выражение в скобках не равно нулю, то соответствующая переменная двойственной задачи в оптимальном плане равна нулю. Напротив, если в оптимальном плане какая-то переменная положительна, то соответствующее ограничение двойственной задачи выполняется как уравнение для любого ее оптимального плана.
Для выяснения смысла этих утверждений допустим, что
т.е. в оптимальном плане выпуска продукции i-й вид ресурса расходуется не полностью, тогда из формулы (3.10) следует, что 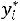
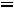
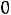 . Это значит, что оценки недефицитных ресурсов равны нулю. С другой стороны, из условия
. Это значит, что оценки недефицитных ресурсов равны нулю. С другой стороны, из условия 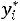
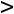
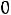 следует, что
следует, что
т.е. соответствующий ресурс расходуется полностью на выпуск продукции и является дефицитным. Таким образом, из положительности оценок ресурсов вытекает их дефицитность.
Аналогичное истолкование можно дать и соотношению (3.9). Действительно, пусть
т. е. суммарная стоимость ресурсов, затраченных на выпуск единицы продукции j-го вида, больше прибыли от ее выпуска, Тогда для обращения в нуль произведения необходимо, чтобы 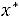
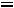
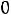 , что означает нецелесообразность выпус-
, что означает нецелесообразность выпус-
ка продукции этого вида. С другой стороны, если 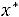
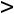
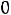 , то
, то
23
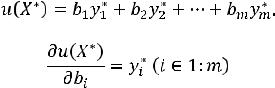
Это значит, что для каждой единицы продукции, выпуск которой целесообразен, суммарная оценка израсходованных ресурсов равна получаемой от его выпуска прибыли.
Отметим еще одну важную роль двойственных оценок. Из формул (3.1), (3.4), (3.8) следует
(3.11)
Рассматривая запас i-го ресурса как переменную величину, получаем
(3.12)
Это показывает, что оценка 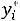 ресурса i-го вида представляет собой скорость возрастания максимальной прибыли при увеличении в некоторых пределах запаса
ресурса i-го вида представляет собой скорость возрастания максимальной прибыли при увеличении в некоторых пределах запаса 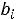 этого ресурса.
этого ресурса.
Для недефицитного ресурса 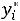
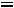
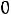 , и увеличение его запаса не приводит к росту прибыли. Напротив, целесообразно стремиться к увеличению в некоторых пределах тех ресурсов, для которых оценки положительны, т.е.
, и увеличение его запаса не приводит к росту прибыли. Напротив, целесообразно стремиться к увеличению в некоторых пределах тех ресурсов, для которых оценки положительны, т.е. 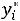
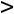
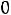 . В соответствии с формулой (3.12), это вызовет возможность увеличения максимальной прибыли.
. В соответствии с формулой (3.12), это вызовет возможность увеличения максимальной прибыли.
Таким образом, объективно обусловленные оценки, являясь стимулом оптимального выпуска продукции при имеющихся запасах ресурсов, в то же время указывают путь к проведению организационных мероприятий, связанных с приобретением дополнительного количества ресурсов определенного вида. Кроме получения большой экономической информации, переход к двойственной задаче может оказаться полезным и с точки зрения трудоемкости получаемого решения. Например, если в исходной задаче всего два основных ограничения и больше двух переменных, то целесообразен переход к двойственной задаче, так как в ней содержатся всего две переменные и ее можно решить графически. Если найдено решение двойственной задачи, то решение исходной задачи можно получить, используя соотношения дополняющей нежесткости.
Трудность решения задач ЛП симплекс-методом в большей степени возрастает с увеличением числа основных ограничений и в меньшей - с увеличением числа переменных. Поэтому, если в исходной задаче количество ограничений велико по сравнению с числом неизвестных, то сначала легче получить решение двойственной задачи.
Планирование оптимального объема добычи
Три шахты, входящие в объединение, поставляют энергетический и коксующийся угли. Добыча этих видов угля в целом по объединению с учетом круга потребителей не должна превышать 40 тыс. и 15 тыс. т. соответственно. Известно, что энергетический уголь в общем объеме добычи по шахтам составляет соответственно 60, 80. и 30 %, а величина прибыли 4,8; 3,2; 4,2 руб. в расчете на 1 т угля.
Требуется определить объемы добычи каждой шахты таким образом, чтобы обеспечить получение максимальной прибыли по объединению.
24

Составим математическую модель задачи, обозначив через 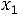 ,
, 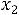 ,
, 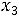 - искомые объемы добычи трех шахт.
- искомые объемы добычи трех шахт.
Целевая функция - суммарная прибыль по объединению.
Ограничения:
а) по добыче энергетического угля
б) по добыче коксующегося угля
в) по неотрицательности искомых величин
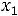
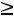
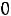
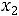
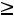
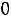
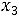
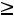
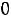 .
.
Пусть 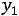 - оценка стоимости 1 т энергетического угля, а
- оценка стоимости 1 т энергетического угля, а 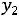 - коксующегося. Тогда можно составить следующую двойственную задачу.
- коксующегося. Тогда можно составить следующую двойственную задачу.
Целевая функция - суммарная оценка всего добываемого угля
Ограничения:
а) по рентабельности добычи на каждой шахте
б) по неотрицательности оценок:
Оптимальный план двойственной задачи находим с помощью инструмента Поиск решения. Сначала создаем исходную таблицу, вносим в нее исходные данные и необходимые формулы (рис.3.1).
Рис.3.1. Ввод исходных данных и формул
Указав в окне параметров соответствующие ограничения, получим реше-
ние (рис.3.2).
Рис. 3.2. Решение двойственной задачи
25
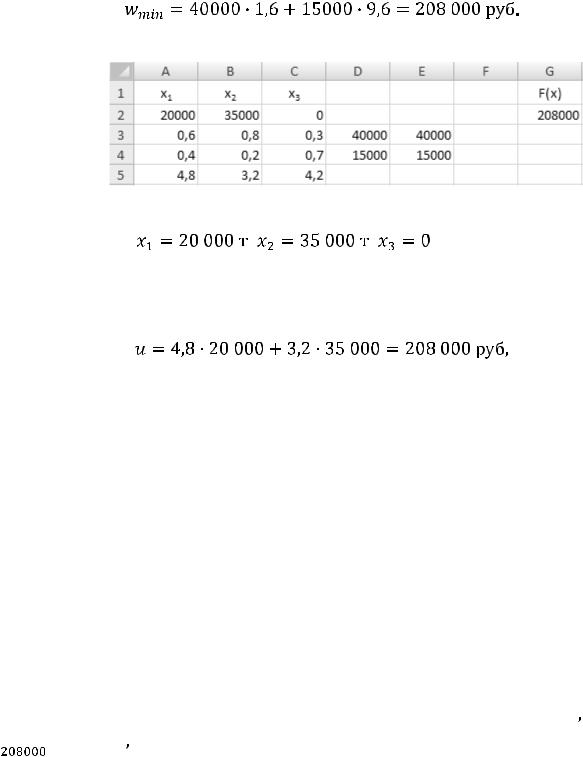
Оценки стоимости энергетического и коксующегося углей, объективно обусловленные для данного объединения, равны соответственно  = 1,6 руб/т,
= 1,6 руб/т, 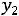 = 9,6 руб/т. Суммарная минимальная оценка всего добываемого по объединению угля составляет
= 9,6 руб/т. Суммарная минимальная оценка всего добываемого по объединению угля составляет
Решение исходной задачи находим таким же образом (рис.3.3).
|
Рис. 3.3. Решение исходной задачи |
||
Получаем, |
, |
, |
. |
Следовательно, в данных условиях объединению выгодно добывать с первой и второй шахт соответственно 20 тыс. и 35 тыс. т угля. Вести добычу на третьей шахте нецелесообразно. Такое планирование позволяет получить объединению максимально возможную прибыль в размере
что совпадает с общей минимальной оценкой добываемого угля и согласуется с теорией двойственности, подтверждая оптимальность полученных решений обеих задач.
О неочевидности полученного результата говорит то, что удельная прибыль по третьей шахте выше, чем по второй и, казалось бы, выгоднее планировать добычу не по второй, а по третьей шахте. Однако интуиция здесь подводит. Из полученного решения следует, что любой допустимый в данных условиях вариант плана добычи приведет к меньшей суммарной прибыли по объединению. Это свидетельствует о силе методов линейного программирования, позволяющих находить иногда неочевидные варианты планирования.
Ненулевые значения полученных оценок угля обоих видов свидетельствуют о том, что они дефицитны: они находят полный сбыт у данного круга потребителей, обеспечивая их полностью; увеличение спроса в некоторых пределах как на энергетический, так и на коксующийся уголь позволит увеличить максимальную прибыль объединения.
Пусть, например, потребность в энергетическом угле возрастает на 1000 т. Тогда максимальная прибыль увеличится на 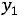

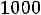
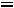
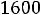
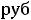
 т.е. на
т.е. на
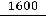

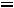
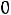
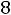
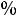 . Прирост на 1000 т потребности в коксующемся угле при
. Прирост на 1000 т потребности в коксующемся угле при
оптимальном планировании добычи вызовет увеличение прибыли по объединению на 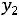

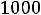
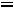
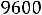
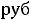
 , т. е. на
, т. е. на 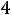
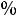 .
.
Отметим, что если в условиях задачи задать иные соотношения объемов добычи энергетического и коксующегося углей на шахтах или существенно из-
26
менить спрос на них, то после решения двойственной задачи одна из оценок может оказаться равной нулю.
Это будет означать недефицитность спроса для соответствующего вида углей: увеличение спроса на него не приводит к увеличению прибыли объединения, поскольку уголь и так находит полный сбыт, а потребности данного круга потребителей удовлетворяются не полностью.
Следует отдельно остановиться на том, что в соответствии с полученным решением, по третьей шахте добыча угля не должна планироваться совсем. Если шахты — проектируемые, то такое решение не вызывает особых возражений, если же шахта — действующая, то это означает ее фактическое закрытие, что на практике может оказаться неприемлемым с учетом факторов, не принятых во внимание при постановке данной задачи. Это свидетельствует о том, что получаемые математическими методами решения являются оптимальными только в пределах условий рассмотренных при постановке задачи.
Таким образом, возможный недостаток полученного решения свидетельствует не о слабости методов линейного программирования, а о том, что постановке задачи не было уделено необходимого внимания.
Глава 4. Транспортная задача
При планировании объемов перевозок, определении загрузки оборудования, распределении трудовых ресурсов, построении сетей вскрывающих и подготовительных выработок и при решении других задач горного производства возникает одна из типичных задач линейного программирования, которую относят к классу транспортных задач. В одних случаях это означает определение такого плана перевозок, при котором стоимость последних была бы минимальна, а в других более важным является выигрыш во времени. Первая задача получила название транспортной задачи по критерию стоимости, а вторая - транспортной задачи по критерию времени.
Транспортная задача является частным случаем задачи линейного программирования и может быть решена симплексным методом. Однако в силу особенностей переменных этой задачи для ее решения разработаны специальные методы. Наиболее применяемым является метод потенциалов.
Пусть в р пунктах отправления находятся соответственно a1, а2, ... , ар единиц однородного груза, который должен быть доставлен q потребителям в количествах b1, b2, ... bq единиц. Заданы стоимости сik перевозок единицы груза из i-го пункта отправления k-му пункту потребления. Обозначим через хik (i = l, 2,...,р; k = 1, 2, ... , q) количество единиц груза, перевозимого из i-го склада k-му потребителю. Переменные хik должны удовлетворять следующим ограничениям:
а) |
|
(4.1) |
|
27
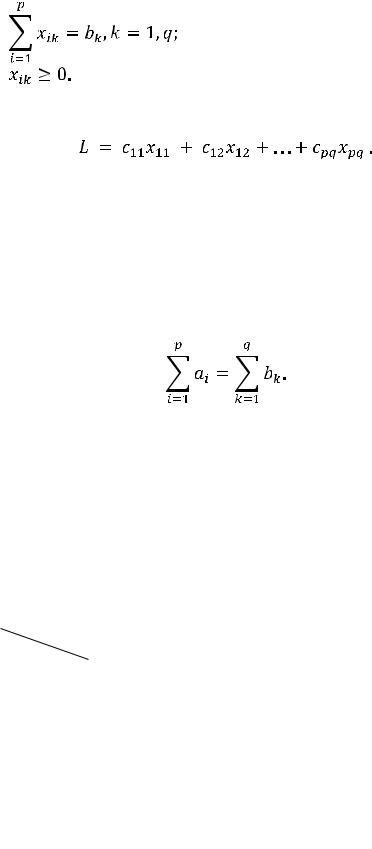
б) |
|
|
(4.2) |
|
|||
в) |
(4.3) |
||
Суммарные затраты на перевозки равны |
|
||
Следовательно, требуется найти pq переменных 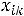 , удовлетворяющих указанным условиям и минимизирующих целевую функцию L.
, удовлетворяющих указанным условиям и минимизирующих целевую функцию L.
Решение такой задачи разбивается на два этапа:
1)определение допустимого исходного базисного решения;
2)построение последовательных итераций,
т.е. приближение к оптимальному решению.
В рассматриваемой задаче предполагается, что сумма запасов равна сумме потребностей:
Такая задача называется закрытой. Если это условие не выполняется, то задача называется открытой. Для сведения открытой задачи к закрытой вводится или фиктивный пункт отправления или фиктивный пункт потребления.
Определение допустимого исходного базисного решения
Пусть исходные данные задачи занесены в таблицу (табл. 4.1). Наиболее простым из методов построения допустимого исходного базисного решения является метод северо-западного угла.
Таблица 4.1
bk |
|
b1 |
|
b2 |
|
|
bk |
|
|
bq |
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
c11 |
|
c12 |
... |
|
c1k |
... |
|
c1q |
|
x11 |
x12 |
x1k |
x1q |
||||||||
|
|
|
|||||||||
a2 |
|
c21 |
|
c22 |
... |
|
c2k |
... |
|
c2q |
|
x21 |
x22 |
x2k |
x2q |
||||||||
|
|
|
|||||||||
|
.... |
.... |
|
.... |
|
.... |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
аi |
|
ci1 |
|
ci2 |
... |
|
cik |
... |
|
ciq |
|
xi1 |
xi2 |
xik |
xiq |
||||||||
|
|
|
|||||||||
|
|
|
.... |
|
|
|
|
.... |
|||
|
|
|
|
|
|
|
|
|
|
|
|
аp |
|
cp1 |
|
cp2 |
... |
|
cpk |
... |
|
cpq |
|
xp1 |
xp2 |
xpk |
xpq |
||||||||
|
|
|
|||||||||
Заполним таблицу, начиная с левого верхнего угла, двигаясь далее или по строке вправо, или по столбцу вниз. В клетку (1, 1) занесем меньшее из чисел а1
и b1, т.е. x11 = min{а1, b1}.
28

Если а1 > b1, то x11 = b1 и первый столбец «закрыт», т.е. потребности первого потребителя удовлетворены полностью. Двигаемся далее по первой строке, записывая в соседнюю клетку (1, 2) меньшее из чисел а1 - b1 и b2, т.е. . x12 =
min{ а1 - b1 , b2}.
Если же b2 > a1, то аналогично «закрывается» первая строка и далее переходим к заполнению соседней клетки (2, 1), куда заносим x21 = min{а2, b1-a1}. Будем продолжать этот процесс до тех пор, пока на каком-то этапе не исчерпываются ресурсы ар и потребности bq.
Число базисных переменных транспортной задачи равно рангу системы уравнений (4.1), (4.2): r = p + q - 1. Значит, мы должны заполнить p + q – 1 клеток таблицы. Метод северо-западного угла дает допустимое базисное решение, если на каждом шаге заполнения из рассмотрения выпадает или одна строка, или один столбец.
Иногда на некотором шаге из рассмотрения выпадают одновременно и строка и столбец. Допустим, что после заполнения клетки (i, k) из рассмотрения выпадает i-ая строка и k-ый столбец. Для того чтобы получаемое распределение перевозок было допустимым, следует поместить фиктивную (нулевую) перевозку или в клетку (i+1, k), или в клетку (i, k+1).
Допустимое базисное решение, достаточно близкое к оптимальному, можно построить с помощью метода минимальной стоимости.
Сначала заполняется клетка таблицы, соответствующая минимальной стоимости 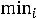
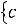
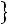 , и исключается из рассмотрения только одна строка или один столбец. Остальные клетки заполняют аналогично методу северозападного угла. Поставщик исключается из рассмотрения, если его ресурсы использованы полностью. Потребитель исключается из рассмотрения, когда его запросы полностью удовлетворены. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда требуется поставить груз от данного поставщика, в соответствующую клетку таблицы записывают базисный нуль, и лишь затем поставщик исключается из рассмотрения. Аналогично поступают и с потребителем.
, и исключается из рассмотрения только одна строка или один столбец. Остальные клетки заполняют аналогично методу северозападного угла. Поставщик исключается из рассмотрения, если его ресурсы использованы полностью. Потребитель исключается из рассмотрения, когда его запросы полностью удовлетворены. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда требуется поставить груз от данного поставщика, в соответствующую клетку таблицы записывают базисный нуль, и лишь затем поставщик исключается из рассмотрения. Аналогично поступают и с потребителем.
Построение последовательных итераций
Получив допустимое исходное базисное решение, перейдем теперь к построению новых базисных решений, улучшающих друг друга: для этого применим метод потенциалов.
Итак, после построения исходного опорного решения все переменные разбиты на две группы: хjl - базисные и хik - свободные; линейная функции стоимости перевозок выразится через свободные переменные так:
(4.4)
Для нахождения коэффициентов 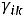 при свободных переменных, сопоставим каждому пункту отправления аi некоторую величину ui (i=1, 2, ... , p), ко-
при свободных переменных, сопоставим каждому пункту отправления аi некоторую величину ui (i=1, 2, ... , p), ко-
29
