Нормальные радиусы скруглений в мм.
0,2 |
0,4 |
0,6 |
1 |
1,6 |
2,5 |
4 |
6 |
10 |
16 |
25 |
40 |
60 |
100 |
160 |
250 |
0,3 |
0,5 |
0,8 |
1,2 |
2 |
3 |
5 |
8 |
12 |
20 |
32 |
50 |
80 |
125 |
200 |
|
К
вадрат.
Перед размерным числом, определяющим
ширину квадрата, ставят знак
,
высота которого равна высоте размерных
чисел. Этот знак наносят, как правило,
на том изображении, на котором квадрат
не проецируется в натуральном виде
(рис. 2.94). Плоская грань поверхности
отмечается на чертеже диагоналями,
проведенными тонкими линиями. На
изображении квадрата, спроецированного
в натуральном виде, предпочтительно
указывать размеры двух его сторон (рис.
2.95, а). Допускается также нанесение
размера квадрата, как показано на
рис. 2.95, б.
Рис. 2.95
Конусность. Перед размерным числом, определяющим конусность, ставят знак , который представляет собой равнобедренный треугольник, острый угол которого направлен в сторону вершины конуса; основание знака равно 4/10 h, а высота – 6/10 h. Построение конусности и примеры ее обозначения будут рассмотрены далее.
У
Рис. 2.100
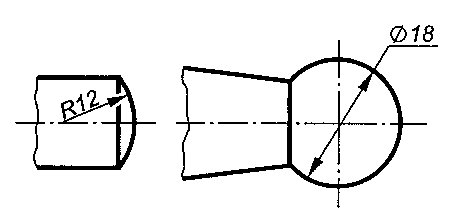
Рис. 2.96
Сфера. Перед размерными числами диаметра или радиуса сферы наносятся знаки ΟR или R без дополнительного знака сферы (рис. 2.96). Знак сферы, представляющий собой окружность с диаметром, равным высоте размерных чисел, наносится перед размерным числом в том случае, если на чертеже трудно отличить сферу от других поверхностей. Тогда размер пишут в виде ΟR10 или R10. Допускается знак сферы заменять словом, например "Сфера R10".
Дуга. При нанесении размера длины дуги окружности над размерным числом всегда ставится знак (см. рис. 2.74).
Н
анесение
размеров фасок. Фасками называются
сплошные (притупленные) кромки стержня,
отверстия, бруска, листа. На чертежах
фаска определяется двумя линейными
(рис. 2.97) или одним линейным и одним
угловым размерами (рис. 2.98).
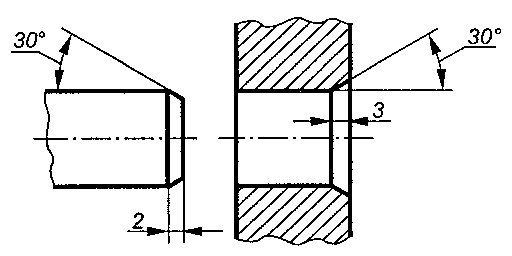
Рис. 2.98
Фаска с углом наклона 45° обозначается двумя размерами: линейным и угловым (рис. 2.99).
Рис. 2.99
Построение и обозначения уклона, конусности
Уклоном называется величина, характеризующая наклон одной прямой по отношению к другой. На рис. 2.100 уклон S прямой ОВ, проведенной под углом к горизонтальной прямой ОА, определяется отношением катетов прямоугольного треугольника АВО (точка В для построения треугольника выбирается произвольно):
S АВ: АО b: a.
Рис. 2.100
Уклон можно также представить в виде дроби, числитель которой должен быть равен единице, или в процентах. Уклон, выраженный в процентах, связан с уклоном, выраженным дробью, формулой:
S % S 100.
Так, например, если S 1:5, то S % 100 20%.
Для проведения некоторой прямой под заданным уклоном к горизонтальной прямой, например 1:3, поступают следующим образом (рис. 2.101, а). На горизонтальной прямой от точки О откладывают три одинаковых отрезка. Из полученной точки А восстанавливают перпендикуляр к ОА и на нем откладывают длину одного отрезка. Уклон полученной прямой ОВ относительно прямой ОА составляет 1:3.
Рис. 2.101
На рис. 2.101, б показано построение уклона, выраженного в процентах (25%), т.е. прямоугольного треугольника, гипотенуза ОВ которого проведена под углом 25% к горизонтальному катету ОА (отношение катета АВ к катету АО равно 1:4, или 25%).
Уклон указывают на полке линии-выноски (см. рис. 2.101, а) либо непосредственно у изображения линии уклона (рис. 2.101, б), при этом перед размерным числом, определяющим уклон, ставят знак , острый угол которого должен быть направлен в сторону уклона. Стандартизованные (ГОСТ 8593–81) значения уклонов приведены в таблице 2.8.
Таблица 2.8