§ 1. Непрерывные одномерные и многомерные случайные величины. Плотность распределения вероятностей.

Случайная величина называется непрерывной, если она может принимать все значения из некоторого конечного или бесконечного промежутка.

Закон распределения вероятностей непрерывной случайной величины определяется функцией - плотностью распределения вероятностей. И вероятность попадания возможных значений непрерывной случайной величины в любой интервал вычисляется по формуле:

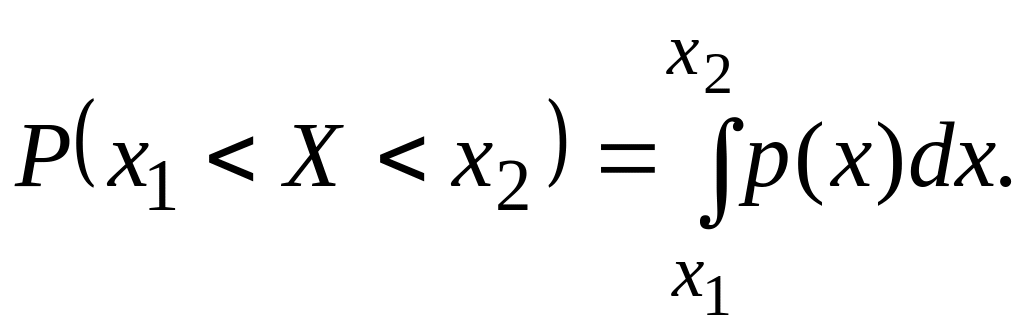
Причем - условие нормировки.

Отметим также, что, в силу определения непрерывной случайной величины, вероятности событий вида:

,

равны между собой.

§ 2. Числовые характеристики непрерывных случайных величин

Если все возможные значения случайной величины X принадлежат интервалу ( ), то

 (X) =

Если же возможные значения непрерывной случайной величины X принадлежат конечному интервалу , то пределы интегрирования в приведенных выше формулах заменяются соответственно: на  , на  .

§ 3. Функция распределения вероятностей и ее свойства

Функцией распределения вероятностей называют функцию , определяемую формулой:

.

Если - непрерывная случайная величина, то

.

Если - дискретная случайная величина, то

.

Функция распределения вероятностей позволяет вычислять вероятность попадания возможных значений непрерывной случайной величины в интервал по формуле:

.

В некоторых приложениях теории вероятностей, в частности, в страховой математике, широко используется характеристика, называемая функцией выживания:

,

которая определяет вероятность того, что случайно взятый человек проживет по крайней мере х лет. Здесь случайная величина означает продолжительность жизни случайно взятого человека.

Например, наглядное представление о продолжительности жизни населения США дает следующая таблица:

0	1	30	0,965	60	0,837	90	0,142
10	0,983	40	0,949	70	0,682	100	0,012
20	0,977	50	0,915	80	0,432	110	0

№ 100. Дискретная случайная величина задана законом распределения вероятностей

	3	5	7
	0,3	0,2	0,5

Найти функцию распределения вероятностей и построить ее график.

Решение. По формуле

получаем:

Построим график этой функции:

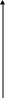
1

0,5

0,3

0 3 5 7 х

№ 101. Непрерывная случайная величина задана функцией распределения вероятностей . Требуется:

а) найти плотность распределения вероятностей ;

б) найти математическое ожидание ;

в) найти дисперсию и среднее квадратическое отклонение ;

г) вычислить вероятность попадания значений случайной величины в интервал (-2, 6);

д) построить графики функции распределения и плотности распределения вероятностей .

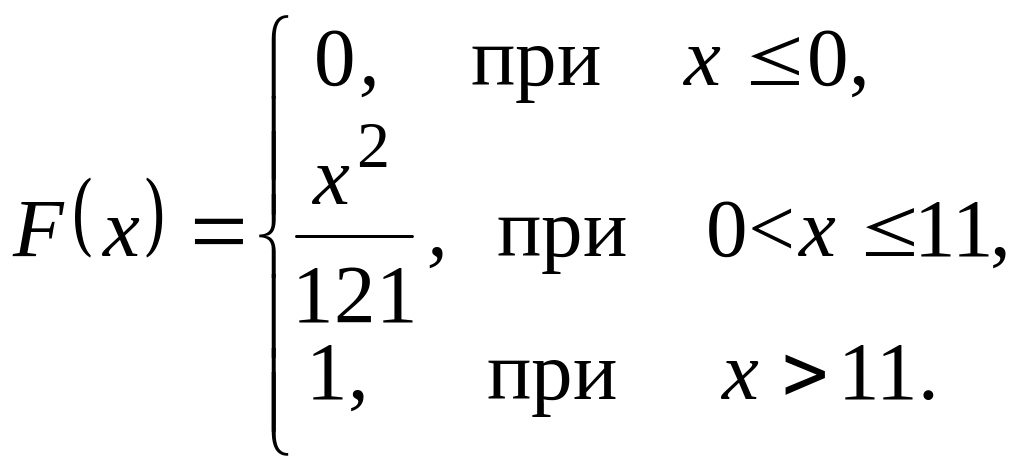
Решение. а) Так как , то

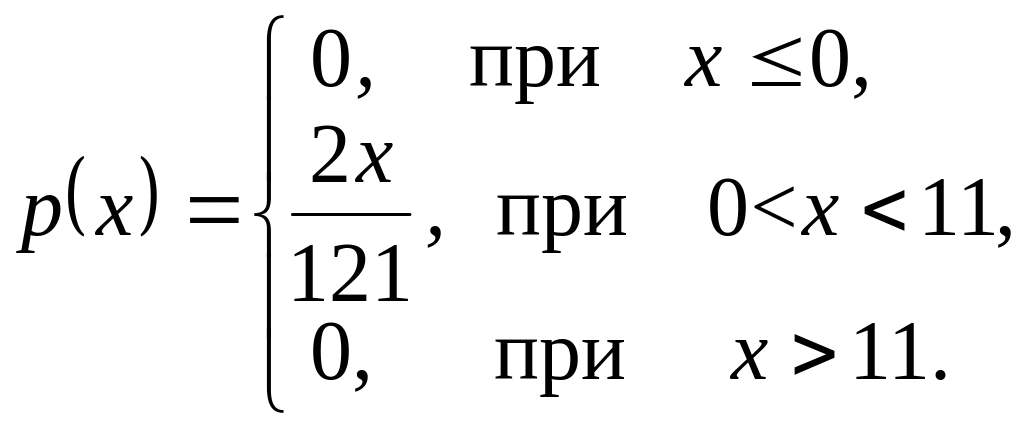
б) Найдем математическое ожидание:

.

в) Вычислим дисперсию:

.

и среднее квадратическое отклонение

.

г) Вероятность может быть вычислена по формулам:

,

или

.

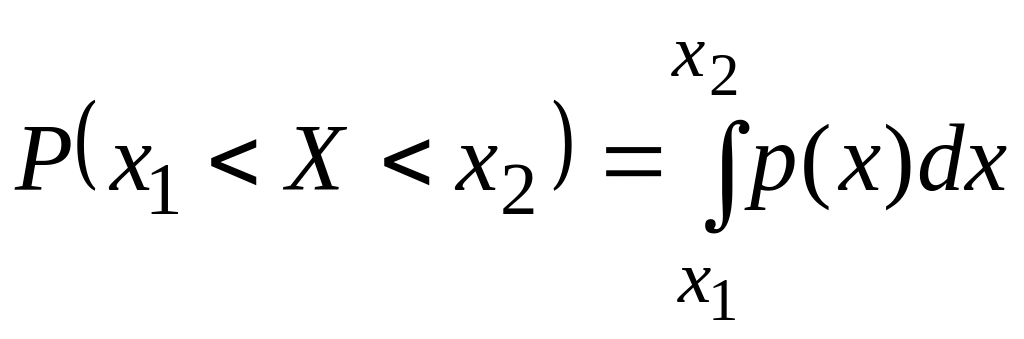Тогда имеем

,

так как , при .

Или

д) График функции :

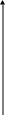
1

0 11

График функции :

0 11

Ответ: б) M(X)=7,33; в) D(X)=6,72;  (X)=2,59; г) 0,3.

№ 102 - 103. Задана плотность распределения вероятностей непрерывной случайной величины X. Найти функцию распределения вероятностей F(x) и построить ее график.

№ 102. 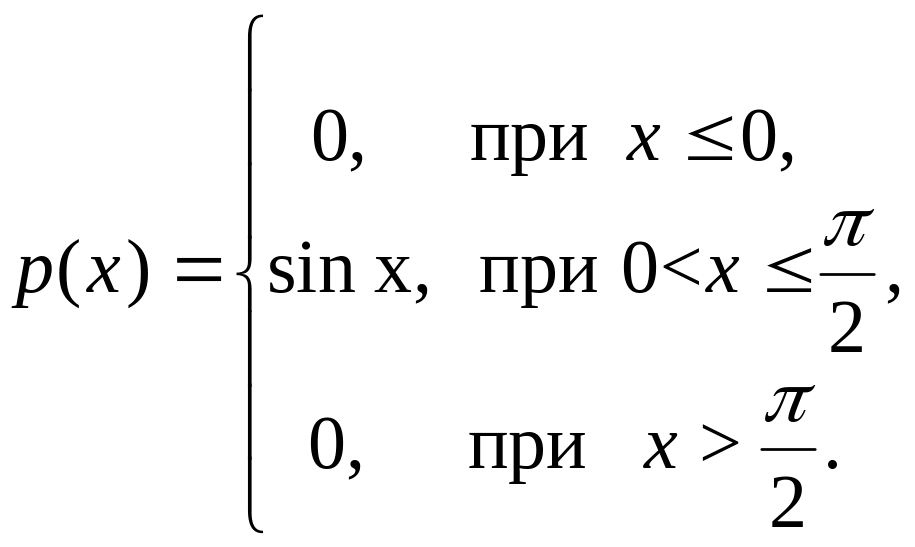№ 103.

№ 104. Случайная величина X задана плотностью распределения в интервале , вне этого интервала . Найти:

а) параметр c; б) числовые характеристики; в) вероятность попадания случайной величины в интервал .

№ 105. Случайная величина X задана плотностью распределения в интервале ; вне этого интервала . Найти числовые характеристики X.

№ 106. Плотность распределения непрерывной случайной величины X равна в интервале ; вне этого интервала . Найти вероятность того, что в трех независимых испытаниях X примет значение, заключенное в интервале : а) ровно два раза; б) хотя бы один раз.

№ 107. По данным таблицы функции выживания вычислите: а) вероятность смерти случайно взятого человека в промежутках и лет; б) условную вероятность смерти для лиц в промежутках и лет, доживших соответственно до 60 и 90 лет. Проанализируйте полученные результаты.