§ 3. Теорема бернулли. Понятие о пределе по вероятности

Частным случаем неравенства Чебышева является неравенство Бернулли:

,

где - относительная частота появления события A в n испытаниях, проводимых по схеме Бернулли с вероятностью появления события A в одном испытании.

Из этого неравенства следует теорема Бернулли вида:

,

или в виде так называемого предела по вероятности:

.

№ 156. Из 1000 изделий, поступивших на склад, были подвергнуты исследованию 200, отобранных случайным образом. Среди них оказалось 25 бракованных. Приняв долю бракованных изделий среди отобранных за вероятность изготовления бракованного изделия, оценить вероятность того, что во всей партии бракованных изделий окажется от 10% до 15%.

Решение. Определим вероятность изготовления бракованного изделия

.

Так как

,

или

,

то, согласно неравенству Бернулли, получаем:

Ответ. .

№ 157. Сколько следует проверить деталей, чтобы с вероятностью не меньшей 0,98 можно ожидать, что абсолютная величина отклонения относительной частоты годных деталей от вероятности деталей быть годной (равной 0,95) не превысит: а) 0,01; б) 0,03; в) 0,05? Проанализируйте полученные результаты.

§4. Асимптотически нормальные распределения и понятие о центральной предельной теореме ляпунова

Пусть дана бесконечная последовательность случайных величин Z₁, Z₂, ... , , ... , где и - независимые случайные величины.

Говорят, что случайные величины имеют асимптотически нормальные распределения с параметрами и , если закон распределения случайной величины , при стремится к стандартному нормальному распределению.

В центральной предельной теореме Ляпунова рассматриваются суммы , и устанавливаются условия, при которых эта сумма имеет асимптотически нормальное распределение.

§ 5. Теорема муавра-лапласа и асимптотика биномиального распределения

Для биномиального распределения вероятностей существует предельное (при ) распределение и это распределение является нормальным.

Значение этой теоремы определяется тем, что при больших n расчет по формуле Бернулли

становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события) , а неравенств вида .

По теореме Муавра-Лапласа следует, что:

,

где

,

- плотность стандартного нормального распределения (приложение 1).

А вероятность сложного события вычисляется как:

,

где - функция Лапласа (приложение 2),

, .

В частности, по теореме Муавра-Лапласа можно оценить отклонение относительной частоты появления события A от вероятности в n независимых испытаниях:

.

№ 158. Вероятность появления некоторого события в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появится: а) ровно 75 раз; б) не менее 50 раз, но не более 85 раз.

Решение. а) Применим формулу

где

По таблице (приложение 1) находим

.

Следовательно,

.

б) Применим формулу:

,

где ,

Следовательно,

.

Ответ: а) 0,04565; б) 0,8944.

№ 159. Страховая компания заключила 1500 договоров краткосрочного (сроком на 1 год) страхования жизни, согласно которым она выплачивает 10 000 руб. в случае смерти застрахованного в течение года и не платит ничего в противном случае. Найти величину индивидуального страхового взноса, обеспечивающего вероятность не разорения компании в 95%. Предполагается, что вероятность смерти, каждого из застрахованных в течение года, постоянна и равна 0,005.

Решение. Будем считать индивидуальные иски , :

	0	10000
	0,995	0,005

к страховой компании независимыми, так как вероятность смерти каждого застрахованного одна и та же. То есть, исключаем экстремальные ситуации (эпидемии, землетрясения и т.д.). Тогда суммарный иск к страховой компании

будет иметь асимптотически нормальное распределение с параметрами:

руб.,

руб.

Следовательно, капитал компании (сумма страховых взносов), обеспечивающая ей вероятность неразорения в 95% будет вычисляться из условия:

,

или

Воспользовавшись приложением № 2, получаем

руб.

Таким образом, индивидуальный страховой взнос, обозначаемый как будет равен:

руб.

Ответ: 79,96 руб.

№ 160. Вероятность того, что деталь не пройдет проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется не прошедших проверку ОТК: а) ровно 85 деталей; б) не менее 70, но не более 95 деталей.

№ 161. Решите № 152 по теореме Муавра-Лапласа и сравните полученные результаты.

№ 162. Решите № 156 по теореме Муавра-Лапласа и сравните полученные результаты.

№ 163. При установившемся технологическом процессе вероятность изготовления бракованных гильз равна 0,05. Для обоснования введения автоматического контроля необходимо определить количество гильз n, которое нужно направлять на контроль, чтобы с вероятностью 0,95 быть уверенным в стабильности технологического процесса, если допускается: а)7% брака; б) 10% брака. Проанализируйте результаты.

№ 164. Накануне референдума было принято решение о проведении социологического опроса. Примерное распределение голосов было известно – около 20% воздержавшихся, остальные примерно поровну “за” и ”против”. Сколько человек надо опросить, чтобы гарантировать отклонение числа ответивших “за” от истинного значения не более чем на 4%, с надежностью в: а) 95%; б) 99%. Проанализируйте результаты.

№ 165. Страховая компания заключила 1000 договоров краткосрочного страхования жизни, согласно которым она выплачивает 15000 руб. в случае смерти застрахованного в течение года и не платит ничего в противном случае. Найти величину индивидуального страхового взноса, обеспечивающего вероятность не разорения компании в а) 95 %; б) 99 %. Предполагается, что вероятность смерти, каждого из застрахованных в течение года, постоянна и равна 0,004.

Г Л А В А VI

Ц Е П И М А Р К О В А

Цепью Маркова называется последовательность испытаний, в каждом из которых система принимает только одно из n состояний полной группы, причем условная вероятность того, что в -ом испытании система будет находиться в состоянии при условии, что после - го испытания она находилась в состоянии , не зависит от результатов ранее проведенных испытаний.

Если вероятности не зависят от номера испытания k, то цепь Маркова называется однородной, а вероятности называются переходными вероятностями.

Матрицей перехода системы называется матрица, составленная из переходных вероятностей вида

.

Здесь сумма вероятностей по строкам равна 1.

Зная матрицу перехода системы из состояния в состояние за один шаг, можно найти матрицу перехода из состояния в состояние за k шагов по формуле:

.

Если - вектор вероятностей состояний на k-ом шаге , то

,

или

.

№ 166. Задана матрица перехода системы

.

Найти матрицы перехода и .

Решение.

,

.

№ 165. Пусть начальный вектор вероятностей состояний цепи Маркова равен . В условиях № 164 найти векторы вероятностей состояний на 1-м, 2-м и 3-м шагах.

Решение.

,

,

.

Из этих примеров видно, что для некоторых цепей Маркова с увеличением номера испытания k, вектор вероятностей состояний изменяется незначительно, и влияние начального вектора состояний становится ничтожно малым. Такие цепи Маркова называются эргодическими.

В этом случае вектор состояний , при , будет вычисляться по формуле:

,

или в виде системы уравнений:

№. 168. Найти вектор предельных вероятностей в условиях № 166.

Решение. Для вычисления вектора предельных вероятностей составим систему уравнений

решив которую, получаем

.

Сравнение с из № 167 показывает, что действительно вектор вероятностей состояний меняется мало.

№ 169. Зная и , найти , , , , , .

№ 170. Завод выпускает телевизоры определенной марки. В зависимости от того, находит ли данный тип телевизора спрос у населения, завод может в конце года находится в одном из двух состояний: – спрос есть, – спроса нет. С течением времени спрос изменяется, так что имеется вероятность 0,8 того, что в конце года завод останется в состоянии . С другой стороны, если завод оказался в состоянии , то принимаются меры к улучшению качества выпускаемой модели, так что с вероятностью 0,6 к концу следующего года завод перейдет в состояние .определить динамику изменения вектора состояний завода, если в начальный момент времени он находился в состоянии: а) ; б) .

№ 171. В учениях участвуют два корабля, которые одновременно производят выстрелы друг в друга через равные промежутки времени. При каждом обмене выстрелами корабль А поражает корабль В с вероятностью 0,5, а корабль В поражает корабль А с вероятностью 0,375. Рассматриваются результаты серии выстрелов. Найти матрицу вероятностей перехода, если состояниями цепи являются: - оба корабля в строю, - в строю корабль А, - в строю корабль В, - оба корабля поражены.

ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ

№ 1. Брошены две игральные кости. Найти вероятности того, что сумма выпавших очков: а) равна k₁; б) равна k₁, а разность k₂; в) равна k₁, если известно, что их разность равна k₂; г) равна k₁, а произведение - k₃; д) не менее k₄.

1.1. k₁=5, k₂=2, k₃=6, k₄=9.

1.2. k₁=6, k₂=3, k₃=5, k₄=10.

1.3. k₁=7, k₂=3, k₃=10, k₄=11.

1.4. k₁=8, k₂=4, k₃=12, k₄=9.

1.5. k₁=9, k₂=4, k₃=8, k₄=10.

1.6. k₁=10, k₂=5, k₃=25, k₄=11.

1.7. k₁=6, k₂=2, k₃=6, k₄=9.

1.8. k₁=7, k₂=2, k₃=12, k₄=10.

1.9. k₁=8, k₂=3, k₃=16, k₄=11.

1.10. k₁=9, k₂=3, k₃=20, k₄=9.

№ 2. Среди n лотерейных билетов k выигрышных. Наудачу взяли m билетов. Определить вероятность того, что среди них l выигрышных.

2.1. n=10, k=3, m=5, l=2. 2.6. n=10, k=4, m=5, l=4.

2.2. n=11, k=4, m=6, l=3. 2.7. n=11, k=5, m=6, l=2.

2.3. n=12, k=5, m=5, l=4. 2.8. n=12, k=6, m=5, l=3.

2.4. n=13, k=6, m=5, l=3. 2.9. n=13, k=7, m=6, l=4.

2.5. n=15, k=7, m=6, l=2. 2.10. n=14, k=4, m=5, l=2.

№ 3. Моменты начала двух событий наудачу распределены в промежутке времени от T₁ до T₂ (час.). Одно из событий длится 10 мин., другое - t мин. Определить вероятность того, что: а) события “перекрываются” по времени; б) “не перекрываются” по времени.

3.1. T₁=9, T₂=10, t=20. 3.6. T₁=14, T₂=16, t=10.

3.2. T₁=10, T₂=11,5, t=15. 3.7. T₁=15, T₂=16,5, t=15.

3.3. T₁=11, T₂=13, t=10. 3.8. T₁=8, T₂=9, t=20.

3.4. T₁=12, T₂=14,5, t=5. 3.9. T₁=7, T₂=7,5, t=25.

3.5. T₁=13, T₂=16, t=5. 3.10. T₁=6, T₂=9,5, t=30.

№ 4. Курс акций каждого из двух предприятий возрастает на 10 пунктов с вероятностью p₁ и убывает на 10 пунктов с вероятностью p₂. Каковы вероятности выигрыша и проигрыша при покупке двух акций различных предприятий.

4.1. p₁=0,30, p₂=0,25. 4.6. p₁=0,15, p₂=0,25.

4.2. p₁=0,25, p₂=0,20. 4.7. p₁=0,20, p₂=0,30.

4.3. p₁=0,20, p₂=0,15. 4.8. p₁=0,25, p₂=0,10.

4.4. p₁=0,15, p₂=0,10. 4.9. p₁=0,30, p₂=0,15.

4.5. p₁=0,10, p₂=0,20. 4.10. p₁=0,10, p₂=0,30.

№ 5. Стрелок производит n выстрелов по удаляющейся цели, причем вероятность поражения цели первым выстрелом равна p₁, а при каждом следующем выстреле уменьшается на p₂. Найти вероятность того, что: а) цель будет поражена только k-м выстрелом; б) цель будет поражена.

5.1. n=4, p₁=0,7, p₂=0,1, k=2.

5.2. n=3, p₁=0,6, p₂=0,2, k=3.

5.3. n=4, p₁=0,8, p₂=0,2, k=3.

5.4. n=3, p₁=0,9, p₂=0,1, k=2.

5.5. n=4, p₁=0,6, p₂=0,1, k=4.

5.6. n=3, p₁=0,7, p₂=0,2, k=3.

5.7. n=4, p₁=0,8, p₂=0,2, k=2.

5.8. n=3, p₁=0,8, p₂=0,1, k=4.

5.9. n=4, p₁=0,9, p₂ =0,2, k=3.

5.10. n=3, p₁=0,5, p₂=0,2, k=2.

№ 6. По оценкам экспертов вероятности банкротства для выделенных трех предприятий, производящих однотипную продукцию, равны p₁, p₂ и p₃. Найти вероятность банкротства: а) только одного предприятия; б) не менее двух предприятий; в) хотя бы одного предприятия.

6.1. p₁=0,10, p₂=0,15, p₃=0,20.

6.2. p₁=0,15, p₂=0,10, p₃=0,05.

6.3. p₁=0,20, p₂=0,15, p₃=0,20.

6.4. p₁=0,05, p₂=0,10, p₃=0,25.

6.5. p₁=0,10, p₂=0,05, p₃=0,10.

6.6. p₁=0,15, p₂=0,05, p₃=0,15.

6.7. p₁=0,20, p₂=0,10, p₃=0,05.

6.8. p₁=0,25, p₂=0,20, p₃=0,10.

6.9. p₁=0,10, p₂=0,25, p₃=0,15.

6.10. p₁=0,05, p₂=0,30, p₃=0,05.

№ 7. a₁% рабочих не выполняют норму выработки, a₂% рабочих выполняют норму выработки до 110%, a₃% рабочих выполняют норму выработки более, чем на 110%. Определить вероятность того, что: а) взятый наудачу рабочий выполняет или перевыполняет норму выработки; б) три наудачу взятых рабочтх выполняют или перевыполняют норму выработки; в) хотя бы один из трех рабочих не выполняет норму выработки.

7.1. a₁=20%, а₂=45%, а₃=35%.

7.2. а₁=25%, а₂=40%, а₃=35%.

7.3. а₁=30%, а₂=35%, а₃=35%.

7.4. а₁=35%, а₂=50%, а₃=15%.

7.5. а₁=40%, а₂=45%, а₃=15%.

7.6. а₁=20%, а₂=40%, а₃=40%.

7.7. а₁=25%, а₂=35%, а₃=40%.

7.8. а₁=30%, а₂=30%, а₃=40%.

7.9. а₁=35%, а₂=40%, а₃=25%.

7.10. а₁=40%, а₂=35%, а₃=25%.

№ 8. Вероятность появления брака на первом станке равна р₁, на втором - р₂, на третьем - р₃. Производительность первого станка в k раз больше, чем второго, а производительность третьего станка в l раз больше, чем первого. Определить вероятность того, что взятая наудачу деталь окажется бракованной. Взятая наудачу деталь оказалась бракованной. Определить вероятность того, что она изготовлена на первом станке.

8.1. p₁=0,010, p₂=0,020, p₃=0,030, k=2, l=2.

8.2. p₁=0,015, p₂=0,015, p₃=0,025, k=3, l=5.

8.3. p₁=0,020, p₂=0,010, p₃=0,020, k=4, l=3.

8.4. p₁=0,025, p₂=0,030, p₃=0,015, k=2, l=4.

8.5. p₁=0,030, p₂=0,025, p₃=0,010, k=3, l=2.

8.6. p₁=0,025, p₂=0,020, p₃=0,010, k=4, l=3.

8.7. p₁=0,020, p₂=0,015, p₃=0,015, k=5, l=4.

8.8. p₁=0,015, p₂=0,010, p₃=0,020, k=2, l=5.

8.9. p₁=0,010, p₂=0,030, p₃=0,025, k=3, l=3.

8.10. p₁=0,030, p₂=0,025, p₃=0,030, k=4, l=2.

№ 9. В первой урне n₁ белых и m₁ черных шаров, во второй n₂ белых и m₂ черных шаров. Из первой урны во вторую переложено k шаров, затем из второй урны извлечен один шар. Определить вероятность того, что этот шар белый.

9.1. n₁=5, m₁=2, n₂=6, m₂=3, k=3.

9.2. n₁=6, m₁=3, n₂=7, m₂=2, k=2.

9.3. n₁=7, m₁=2, n₂=8, m₂=3, k=3.

9.4. n₁=8, m₁=3, n₂=9, m₂=2, k=2.

9.5. n₁=9, m₁=2, n₂=5, m₂=3, k=3.

9.6. n₁=5, m₁=3, n₂=6, m₂=2, k=2.

9.7. n₁=6, m₁=2, n₂=7, m₂=3, k=3.

9.8. n₁=7, m₁=3, n₂=8, m₂=2, k=2.

9.9. n₁=8, m₁=2, n₂=9, m₂=3, k=3.

9.10. n₁=9, m₁=3, n₂=5, m₂=2, k=2.

№ 10. Вероятность того, что кредит размером до 10 млн. руб. не будет возвращен, равна р₁, для кредита размером свыше 10 млн.руб. эта вероятность равна р₂. Банк выдал n₁ кредитов в 5 млн.руб. и n₂ кредитов в 20 млн.руб. Составить закон распределения случайной величины – числа невозвращенных кредитов из этих выданных. Найти наивероятнейшее число невозвращенных кредитов.

10.1. p₁=0,10, p₂=0,15, n₁=1, n₂=2.

10.2. p₁=0,05, p₂=0,20, n₁=2, n₂=1.

10.3. p₁=0,15, p₂=0,10, n₁=1, n₂=2.

10.4. p₁=0,20, p₂=0,05, n₁=2, n₂=1.

10.5. p₁=0,10, p₂=0,20, n₁=1, n₂=2.

10.6. p₁=0,05, p₂=0,10, n₁=2, n₂=1.

10.7. p₁=0,15, p₂=0,05, n₁=1, n₂=2.

10.8. p₁=0,20, p₂=0,15, n₁=2, n₂=1.

10.9. p₁=0.10, p₂=0,05, n₁=1, n₂=2.

10.10. p₁=0,05, p₂=0,15, n₁=2, n₂=1.

№ 11. Из n экзаменационных вопросов студент подготовил k вопросов. Составить закон распределения случайной величины - числа подготовленных вопросов среди трех вопросов экзаменационного билета. Найти наивероятнейшее число подготовленных вопросов билета.

11.1. n=40, k=25. 11.6. n=50, k=35.

11.2. n=50, k=30. 11.7. n=60, k=40.

11.3. n=60, k=35. 11.8. n=30, k=25.

11.4. n=30, k=20. 11.9. n=40, k=30.

11.5. n=40, k=35. 11.10. n=50, k=45.

№ 12. При производстве некоторого изделия вероятность брака равна р. В этом случае предприятие терпит убыток в k₁ тыс.руб. При изготовлении не бракованного изделия прибыль составляет k₂ тыс.руб. Составить закон распределения случайной величины - прибыли предприятия, если изготовлено четыре изделия.

12.1. p=0,20, k₁=40, k₂=10.

12.2. p=0,25, k₁=45, k₂=15.

12.3. p=0,30, k₁=50, k₂=20.

12.4. p=0,15, k₁=55, k₂=25.

12.5. p=0,10, k₁=60, k₂=15.

12.6. p=0,05, k₁=65, k₂=10.

12.7. p=0,20, k₁=70, k₂=20.

12.8. p=0,25, k₁=75, k₂=25.

12.9. p=0,15, k₁=80, k₂=35.

12.10. p=0,10, k₁=85, k₂=30.

№ 13. Некоторая компания имеет сеть дилеров на бирже. Вероятность того, что дилер будет играть удачно равна р. Найти вероятность того, что из n дилеров окажутся в убытке: а) ровно k дилеров; б) не менее k₁ дилеров; в) не более k₂ дилеров.

13.1. p=0,7, n=5, k=2, k₁=3, k₂=2.

13.2. p=0,8, n=4, k=3, k₁=3, k₂=2.

13.3. p=0,9, n=8, k=5, k₁=2, k₂=2.

13.4. p=0,6, n=6, k=4, k₁=5, k₂=3.

13.5. p=0,7, n=7, k=5, k₁=6, k₂=3.

13.6. p=0,8, n=8, k=6, k₁=7, k₂=3.

7. p=0,9, n=6, k=3, k₁=4, k₂=2.

8. p=0,6, n=5, k=3, k₁=4, k₂=3.

13.9. p=0,7, n=8, k=5, k₁=6, k₂=2.

13.10. p=0,8, n=7, k=4, k₁=5, k₂=2.

№ 14. В среднем a% студентов группы сдают зачет с первого раза. Найти вероятность того, что из n человек, сдававших зачет, с первого раза сдадут: а) ровно k студентов; б) не менее k₁ студентов; в) не более k₂ студентов.

14.1. a=60%, n=9, k=8, k₁=7, k₂=6.

14.2. а=65%, n=6, k=5, k₁=4, k₂=3.

14.3. а=70%, n=8, k=7, k₁=6, k₂=5.

14.4. а=75%, n=7, k=6, k₁=5, k₂=4.

14.5. а=80%, n=9, k=8, k₁=7, k₂=6.

14.6. а=85%, n=6, k=5, k₁=4, k₂=3.

14.7. а=90%, n=8, k=7, k₁=6, k₂=5.

8. а=85%, n=7, k=6, k₁=5, k₂=4.

14.9. а= 80%, n=9, k=8, k₁=7, k₂=6.

14.10. а=75%, n=6, k=5, k₁=4, k₂=3.

№ 15. Вероятность того, что 100-долларовая купюра фальшивая равна р. Найти вероятность того, что из n купюр: а) ровно k фальшивых купюр; б) не менее k₁ фальшивых купюр; в) хотя бы одна купюра фальшивая.

15.1. p=0,01, n=100, k=2, k₁=3.

15.2. p=0,02, n=200, k=5, k₁=2.

15.3. p=0,03, n=100, k=4, k₁=1.

15.4. p=0,04, n=200, k=7, k₁=2.

15.5. p=0,05, n=100, k=6, k₁=3.

15.6. p=0,01, n=200, k=1, k₁=1.

15.7. p=0,02, n=100, k=3, k₁=1.

15.8. p=0,03, n=200, k=9, k₁=2.

15.9. p=0,04, n=100, k=8, k₁=3.

15.10. p=0,05, n=200, k=7, k₁=2.

№ 16. Семена содержат 0,1% сорняков. Какова вероятность при случайном отборе из n семян обнаружить: а) ровно k семян сорняков; б) не менее k₁ семян сорняков.

16.1. n=4000, k=5, k₁=3. 16.6. n=4000, k=2, k₁=2.

16.2. n=3000, k=6, k₁=2. 16.7. n=3000, k=3, k₁=3.

16.3. n=2000, k=4, k₁=3. 16.8. n=2000, k=4, k₁=2.

16.4. n=1000, k=3, k₁=2. 16.9. n=1000, k=6, k₁=3.

16.5. n=5000, k=2, k₁=3. 16.10. n=5000, k=5, k₁=2.

№ 17.1-17.3. Среднее число самолетов, прибывающих в аэропорт за 1 мин, равно двум. Найти вероятность того, что за 3 мин прибудут: а) ровно k самолетов; б) менее k₁ самолетов; в) не менее k₂ самолетов.

17.1. k=2, k₁=2, k₂=2. 17.3 k=4, k₁=2, k₂=3.

17.2. k=3, k₁=3, k₂=2.

№ 17.4-17.6. Среднее число кораблей, заходящих в порт за 1 час, равно двум. Найти вероятность того, что за 4 часа в порт зайдут: а) ровно k кораблей; б) менее k₁ кораблей; в) не менее k₂ кораблей.

17.4. k=4, k₁=4, k₂=4. 17.6. k=4, k₁=4, k₂=5.

17.5. k=5, k₁=5, k₂=4.

№ 17.7-17.10. Среднее число вызовов, поступающих на АТС за одну минуту, равно двум. Найти вероятность того, что за четыре минуты поступит: а) ровно k вызовов; б) менее k₁ вызовов; в) не менее k₂ вызовов.

17.7. k=3, k₁=4, k₂=4. 17.9. k=3, k₁=4, k₂=3.

17.8. k=4, k₁=3, k₂=4. 17.10. k=4, k₁=3, k₂=3.

№ 18. Задан закон распределения дискретной случайной величины Х. Найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение; г) функцию распределения вероятностей и построить ее график.

18.1.	X	25	27	28	30		18.2	X	19	22	23	25
	p	0,4	0,3	0,2	0,1			p	0,3	0,4	0,2	0,1

18.3.	X	31	32	35	37		18.4.	X	18	24	25	30
	p	0,2	0,2	0,1	0,5			p	0,6	0,1	0,1	0,2

18.5.	X	26	31	32	35		18.6.	X	6	9	15	21
	p	0,4	0,4	0,1	0,1			p	0,2	0,1	0,1	0,6

18.7.	X	15	17	18	21		18.7.	X	17	22	23	25
	p	0,2	0,3	0,2	0,3			p	0,7	0,1	0,1	0,1

18.9.	X	24	25	27	30		18.10.	X	21	22	30	32
	p	0,3	03	0,1	0,3			p	0,2	0,4	0,1	0,3

№ 19. Задана дискретная двумерная случайная величина (X, Y). Найти: а) безусловные законы распределения составляющих; б) условные математические ожидания M(Y|X=x₁) и M(X|Y=y₂).

19.1.	X Y	1	2		19.2.	X Y	1	3
	0	0,10	0,15			-1	0,05	0,15
	2	0,20	0,10			1	0,10	0,25
	3	0,30	0,15			4	0,35	0,10

19.3.	X Y	4	5		19.4.	X Y	4	6
	3	0,10	0,35			4	0,25	0,40
	4	0,15	0,05			5	0,05	0,05
	5	0,20	0,15			6	0,10	0,15
19.5.	X Y	2	5		19.6.	X Y	2	4
	5	0,30	0,05			6	0,15	0,30
	6	0,25	0,10			7	0,20	0,05
	7	0,20	0,10			8	0,25	0,05

19.7.	X Y	-1	3		19.8.	X Y	-1	2
	-2	0,10	0,25			-1	0,50	0,05
	-1	0,15	0,25			0	0,10	0,15
	0	0,05	0,20			1	0,05	0,15

19.9.	X Y	0	5		19.10.	X Y	0	3
	0	0,05	0,30			1	0,15	0,25
	1	0,25	0,15			2	0,20	0,10
	2	0,10	0,15			3	0,10	0,20

№ 20. Непрерывная случайная величина задана функцией распределения вероятностей F(х). Требуется: а) найти плотность распределения вероятностей р(х); б) найти математическое ожидание, дисперсию и среднее квадратическое отклонение; в) вычислить вероятность попадания случайной величины в интервал (а, b); г) построить графики функции распределения F(х) и плотности распределения р(х).

20.1. 20.2.

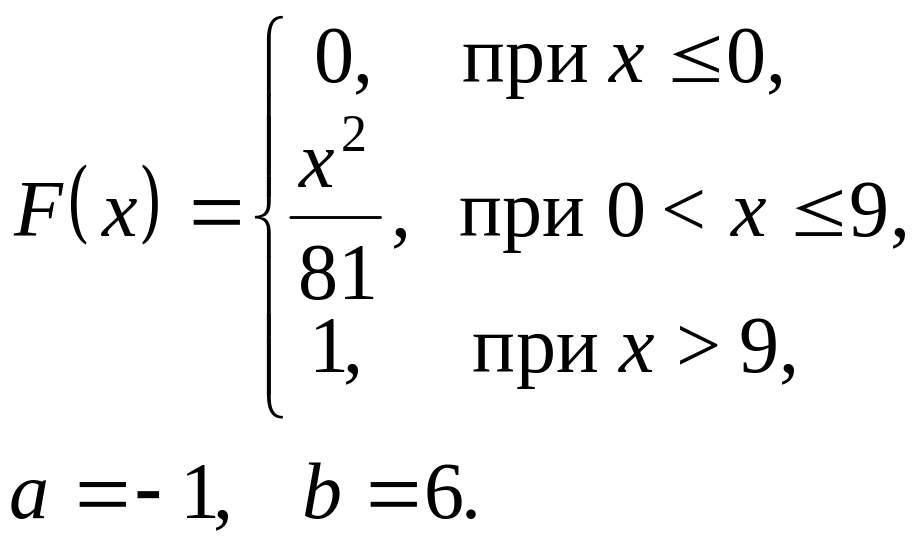
20.3. 20.4.

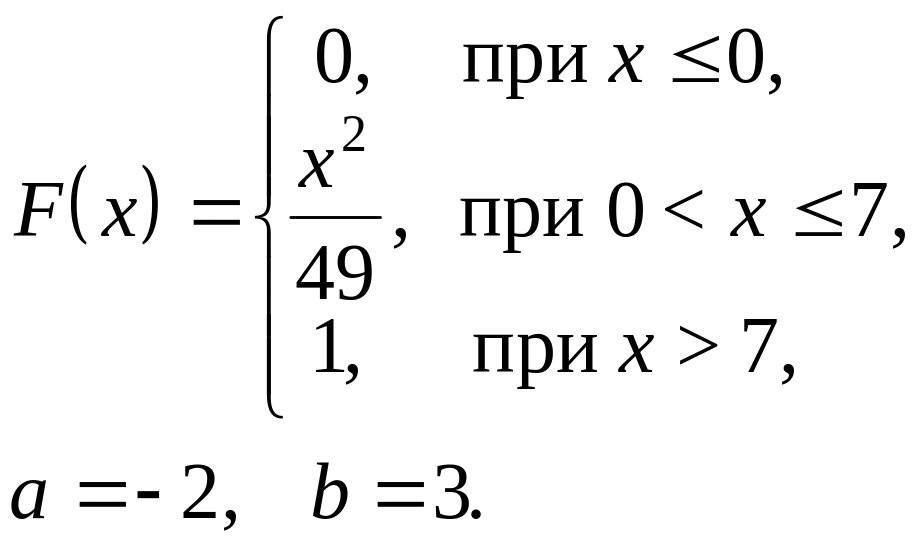
20.5. 20.6.

20.7. 20.8.

20.9. 20.10.

№ 21. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента ; для второго ; для третьего - . Найти вероятности того, что в интервале времени (0, Т) откажут: а) все три элемента; б) только два элемента; в) хотя бы один элемент; г) не менее одного элемента.

21.1. ₁=0,01, ₂=0,02, ₂=0,10, Т=2.

21.2. ₁=0,02, ₂=0,03, ₃=0,04, Т=3.

21.3. ₁=0,03, ₂=0,01, ₃=0,05, Т=4.

21.4. ₁=0,04, ₂=0,04, ₃=0,06, Т=5.

21.5. ₁=0,05, ₂=0,06, ₃=0,07, Т=1.

21.6. ₁=0,06, ₂=0,05, ₃=0,02, Т=5.

21.7. ₁=0,07, ₂=0,08, ₃=0,03, Т=4.

21.8. ₁=0,08, ₂=0,10, ₃=0,09, Т=3.

21.9. ₁=0,09, ₂=0,09, ₃=0,08, Т=2.

21.10. ₁=0,10, ₂=0,07, ₃=0,01, Т=1.

№ 22. Детали, выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина детали равна а мм, среднее квадратическое отклонение -  мм. Найти вероятность того, что: а) диаметр наудачу взятой детали больше  мм и меньше  мм; б) диаметр детали отклонится от стандартной длины не более, чем на  мм.

22.1. а=50, =4, =48, =54, =2.

22.2. а=45, =3, =42, =46, =3.

22.3. а=40, =2, =39, =43, =2,5.

22.4. а=35, =2, =33, =36, =3.

22.5. а=30, =3, =27, =32, =2.

22.6. а=25, =3, =22, =27, =2,5.

22.7. а=20, =4, =17, =22, =2.

22.8. а=55, =5, =54, =58, =3.

22.9. а=60, =5, =56, =62, =2,5.

10. а=65, =6, =63, =66, =3.

№ 23. Средняя масса плодов в одном ящике равна а кг, а среднее квадратическое отклонение в массе плодов одного ящика равно  кг. В магазин поступило n ящиков. Приняв во внимание, что масса плодов в одном ящике – нормально распределенная случайная величина, найти: а) вероятность того, что масса плодов в n ящиках окажется не менее m кг; б) наибольшее значение, которое с вероятностью р не превзойдет масса n ящиков плодов.

23.1. a=10, n=200, =1,5, m=1920, p=0,99.

23.2. a=15, n=100, =2, m=1450, p=0,98.

23.3. a=20, n=150, =2,5, m=2960, p=0,97.

23.4. a=10, n=150, =1, m=1440, p=0,96.

23.5. a=15, n=200, =1,5, m=2920, p=0,95.

23.6. a=20, n=100, =2, m=1980, p=0,94.

23.7. a=10, n=100, =2, m=970, p=0,93.

23.8. a=15, n=150, =1, m=2240, p=0,92.

23.9. a=20, n=200, =1,5, m=3990, p=0,91.

23.10. a=10, n=250, =0,5, m=2490, p=0,90.

№ 24. Даны две независимые случайные величины X и Y. Найти законы распределения случайных величин и , и проверить свойства математических ожиданий , .

24.1.	X	2	3	4		Y	1	3	5
	p	0,2	0,6	0,2		g	0,1	0,5	0,4

24.2.	X	3	5	7		Y	2	4	5
	p	0,3	0,3	0,4		g	0,4	0,2	0,4
24.3.	X	5	8	9		Y	2	3	6
	p	0,7	0,2	0,1		g	0,3	0,5	0,2

24.4.	X	4	5	6		Y	1	2	4
	p	0,5	0,3	0,2		g	0,2	0,6	0,2

24.5.	X	1	3	4		Y	1	5	6
	p	0,4	0,5	0,1		g	0,5	0,3	0,2

24.6.	X	2	4	6		Y	3	4	5
	p	0,2	0,3	0,5		g	0,1	0,3	0,6

24.7.	X	3	4	7		Y	1	4	5
	p	0,3	0,3	0,4		g	0,5	0,1	0,4

24.8.	X	1	3	7		Y	2	5	8
	p	0,3	0,6	0,1		g	0,8	0,1	0,1

24.9.	X	2	6	7		Y	1	4	7
	p	0,4	0,4	0,2		g	0,5	0,4	0,1

24.10	X	4	6	8		Y	1	2	3
	p	0,2	0,2	0,6		g	0,3	0,1	0,6

№ 25.1-25.5. В осветительную сеть включено параллельно n лампочек. Вероятность того, что за время t лампа будет включена равна р. Пользуясь неравенством Чебышева оценить вероятность того, что число включенных ламп будет заключено в пределах от k₁ до k₂.

25.1. n=100, p=0,8, k₁=75, k₂=85.

25.2. n=90, p=0,7, k₁=60, k₂=66.

25.3. n=80, p=0,8, k₁=60, k₂=68.

25.4. n=70, p=0,7, k₁=47, k₂=51.

25.5. n=60, p=0,9, k₁=51, k₂=57.

№ 25.6-25.10. При штамповке пластинок из пластмассы брак составляет а%. Оценить снизу вероятность того, что при просмотре партии в n пластинок выявится отклонение от установленного процента брака меньше, чем на b%.

25.6. а=3%, n=1000, b=2%. 25.9. а=8%, n=250, b=5%.

25.7. а=4%, n=500, b=3%. 25.10. а=2%, n=1500, b=1%.

25.8. а=5%, n=400, b=4%.

№ 26. Завод сортовых семян выпускает гибридные семена кукурузы. Известно, что семена первого сорта составляют а%. Определить вероятность того, что из взятых наудачу n семян: а) ровно k семян будет первого сорта; б) будет не менее k₁, но не более k₂ семян первого сорта.

26.1. а=90%, n=200, k=160, k₁=170, k₂=185.

26.2. а=80%, n=250, k=190, k₁=190, k₂=250.

26.3. а=70%, n=300, k=200, k₁=200, k₂=215.

26.4. а=75%, n=350, k=220, k₁=250, k₂=270.

26.5. а=85%, n=400, k=330, k₁=340, k₂=365.

26.6. а=95%, n=200, k=180, k₁=185, k₂=195.

26.7. а=90%, n=250, k=220, k₁=215, k₂=250.

26.8. а=80%, n=300, k=250, k₁=235, k₂=255.

26.9. а=85%, n=350, k=320, k₁=290, k₂=310.

10. а=75%, n=400, k=310, k₁=280, k₂=305.

№ 27. Пусть имеются три конкурирующих изделия , и . Для определения спроса на эти изделия произведен в некоторый начальный момент опрос человек. Оказалось, что изделие покупают человек, - , а - человек. Предположим, что поведение покупателей в каждый следующий месяц обусловлено только их поведением в предыдущий месяц.

По истечении месяца оказалось, что из человек, покупавших изделие , человек продолжают его покупать, человека стали покупать изделие и - изделие .

Из человек, покупавших изделие , человек продолжают его покупать, - стали покупать изделие , а - изделие .

Из человек, покупавших изделие , человек продолжают его покупать, - стали покупать изделие , а - изделие .

Определить, какое изделие будет пользоваться наибольшим спросом: а) через 1 месяц; б) через 2 месяца; в) через 3 месяца; г) по истечении достаточно продолжительного периода.

№	27.1	27.2	27.3	27.4	27.5	27.6	27.7	27.8	27.9	27.10
n	1000	2000	500	1000	2000	500	1000	2000	500	1000
n1	600	800	200	400	1000	100	300	1200	300	500
n2	200	1000	200	500	300	100	400	200	50	300
n3	200	200	100	100	700	300	300	600	150	200
n11	150	200	100	160	400	20	100	900	60	100
n12	300	200	50	100	250	10	150	150	60	200
n13	150	400	50	140	350	70	50	150	180	200
n21	100	500	20	100	150	30	200	40	10	90
n22	50	200	50	300	90	30	50	100	20	30
n23	50	300	130	100	60	40	150	60	20	180
n31	20	100	10	30	140	30	120	240	30	120
n32	40	50	70	20	280	240	90	60	30	20
n33	140	50	20	50	280	30	90	300	90	60

П Р И Л О Ж Е Н И Я

ПРИЛОЖЕНИЕ 1

Таблица значений функции

	0	1	2	3	4	5	6	7	8	9
0,0	0,3989	3989	3989	3988	3986	3984	3982	3980	3977	3973
0,1	3970	3965	3961	3956	3951	3954	3939	3932	3925	3918
0,2	3910	3902	3894	3885	3876	3867	3857	3847	3836	3825
0,3	3814	3802	3790	3778	3765	3752	3739	3726	3712	3697
0,4	3683	3668	3652	3637	3621	3605	3589	3572	3555	3538
0,5	3521	3503	3485	3467	3448	3429	3410	3391	3372	3352
0,6	3332	3312	3292	3271	3251	3230	3209	3187	3166	3144
0,7	3123	3101	3079	3056	3034	3011	2989	2966	2943	2920
0,8	2897	2874	2850	2827	2803	2780	2756	2732	2709	2685
0,9	2661	2637	2613	2589	2565	2541	2516	2492	2468	2444
1,0	0,2420	3296	2371	2347	2323	2299	2275	2251	2227	2203
1,1	2179	2155	2131	2107	2083	2059	2036	2012	1989	1965
1,2	1942	1919	1895	1872	1849	1826	1804	1781	1758	1736
1,3	1714	1691	1669	1647	1626	1604	1582	1561	1539	1518
1,4	1497	1476	1456	1435	1415	1394	1374	3154	1334	1315
1,5	1295	1276	1257	1238	1219	1200	1182	1163	1145	1127
1,6	1109	1092	1074	1057	1040	1023	1006	0989	0973	0957
1,7	0940	0925	0909	0893	0878	0863	0848	0833	0818	0804
1,8	0790	0775	0761	0748	0734	0721	0707	0694	0681	0669
1,9	0656	0644	0632	0620	0608	0596	0584	0573	0562	0551
2,0	0,0540	0529	0519	0508	0498	0488	0478	0468	0459	0449
2,1	0440	0431	0422	0413	0404	0396	0387	0379	0371	0363
2,2	0355	0347	0339	0332	0325	0317	0310	0303	0297	0290
2,3	0283	0277	0270	0264	0258	0252	0246	0241	0253	0229
2,4	0224	0219	0213	0208	0203	0198	0194	0189	0184	0180
2,5	0175	0171	0167	0163	0158	0154	0151	0147	0143	0139
2,6	0136	0132	0129	0126	0122	0119	0116	0113	0110	0107
2,7	0104	0101	0099	0096	0093	0091	0088	0086	0084	0081
2,8	0079	0077	0075	0073	0071	0069	0067	0065	0063	0061
2,9	0060	0058	0056	0055	0053	0051	0050	0048	0047	0046
3,0	0,0044	0043	0042	0040	0039	0038	0037	0036	0035	0034
3,1	0033	0032	0031	0030	0029	0028	0027	0026	0025	0025
3,2	0024	0023	0022	0022	0021	0020	0020	0019	0018	0018
3,3	0017	0017	0016	0016	0015	0015	0014	0014	0013	0013
3,4	0012	0012	0012	0011	0011	0011	0010	0010	0010	0009
3,5	0009	0008	0008	0008	0008	0007	0007	0007	0007	0006
3,6	0006	0006	0006	0005	0005	0005	0005	0005	0005	0004
3,7	0004	0004	0004	0004	0004	0004	0003	0003	0003	0003
3,8	0003	0003	0003	0003	0003	0002	0002	0002	0002	0002
3,9	0002	0002	0002	0002	0002	0002	0002	0002	0001	0001

ПРИЛОЖЕНИЕ 2

Таблица значений функции

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0,00	0,0000	0,35	0,1368	0,70	0,2580	1,05	0,3531
0,01	0,0040	0,36	0,1406	0,71	0,2611	1,06	0,3554
0,02	0,0080	0,37	0,1443	0,72	0,2642	1,07	0,3577
0,03	0,0120	0,38	0,1480	0,73	0,2673	1,08	0,3599
0,04	0,0160	0,39	0,1517	0,74	0,2703	1,09	0,3621
0,05	0,0199	0,40	0,1554	0,75	0,2734	1,10	0,3643
0,06	0,0239	0,41	0,1591	0,76	0,2764	1,11	0,3665
0,07	0,0279	0,42	0,1628	0,77	0,2794	1,12	0,3686
0,08	0,0319	0,43	0,1664	0,78	0,2823	1,13	0,3708
0,09	0,0359	0,44	0,1700	0,79	0,2852	1,14	0,3729
0,10	0,0398	0,45	0,1736	0,80	0,2881	1,15	0,3749
0,11	0,0438	0,46	0,1772	0,81	0,2910	1,16	0,3770
0,12	0,0478	0,47	0,1808	0,82	0,2939	1,17	0,3790
0,13	0,0517	0,48	0,1844	0,83	0,2967	1,18	0,3810
0,14	0,0557	0,49	0,1879	0,84	0,2995	1,19	0,3830
0,15	0,0596	0,50	0,1915	0,85	0,3023	1,20	0,3849
0,16	0,0636	0,51	0,1950	0,86	0,3051	1,21	0,3869
0,17	0,0675	0,52	0,1985	0,87	0,3078	1,22	0,3883
0,18	0,0714	0,53	0,2019	0,88	0,3106	1,23	0,3907
0,19	0,0753	0,54	0,2054	0,89	0,3133	1,24	0,3925
0,20	0,0793	0,55	0,2088	0,90	0,3159	1,25	0,3944
0,21	0,0832	0,56	0,2123	0,91	0,3186	1,26	0,3962
0,22	0,0871	0,57	0,2157	0,92	0,3212	1,27	0,3980
0,23	0,0910	0,58	0,2190	0,93	0,3238	1,28	0,3997
0,24	0,0948	0,59	0,2224	0,94	0,3264	1,29	0,4015
0,25	0,0987	0,60	0,2257	0,95	0,3289	1,30	0,4032
0,26	0,1026	0,61	0,2291	0,96	0,3315	1,31	0,4049
0,27	0,1064	0,62	0,2324	0,97	0,3340	1,32	0,4066
0,28	0,1103	0,63	0,2357	0,98	0,3365	1,33	0,4082
0,29	0,1141	0,64	0,2389	0,99	0,3389	1,34	0,4099
0,30	0,1179	0,65	0,2422	1,00	0,3413	1,35	0,4115
0,31	0,1217	0,66	0,2454	1,01	0,3438	1,36	0,4131
0,32	0,1255	0,67	0,2486	1,02	0,3461	1,37	0,4147
0,33	0,1293	0,68	0,2517	1,03	0,3485	1,38	0,4162
0,34	0,1331	0,69	0,2549	1,04	0,3508	1,39	0,4177
1,40	0,4192	1,70	0,4554	2,00	0,4772	2,60	0,4953
1,41	0,4207	1,71	0,4564	2,02	0,4783	2,62	0,4956
1,42	0,4222	1,72	0,4573	2,04	0,4793	2,64	0,4959
1,43	0,4236	1,73	0,4582	2,06	0,4803	2,66	0,4961
1,44	0,4251	1,74	0,4591	2,08	0,4812	2,68	0,4963
1,45	0,4265	1,75	0,4599	2,10	0,4821	2,70	0,4965
1,46	0,4279	1,76	0,4608	2,12	0,4830	2,72	0,4967
1,47	0,4292	1,77	0,4616	2,14	0,4838	2,74	0,4969
1,48	0,4306	1,78	0,4625	2,16	0,4846	2,76	0,4971
1,49	0,4319	1,79	0,4633	2,18	0,4854	2,78	0,4973
1,50	0,4332	1,80	0,4641	2,20	0,4861	2,80	0,4974
1,51	0,4345	1,81	0,4649	2,22	0,4868	2,82	0,4976
1,52	0,4357	1,82	0,4656	2,24	0,4875	2,84	0,4977
1,53	0,4370	1,83	0,4664	2,26	0,4881	2,86	0,4979
1,54	0,4382	1,84	0,4671	2,28	0,4887	2,88	0,4980
1,55	0,4394	1,85	0,4678	2,30	0,4893	2,90	0,4981
1,56	0,4406	1,86	0,4686	2,32	0,4898	2,92	0,4982
1,57	0,4418	1,87	0,4693	2,34	0,4904	2,94	0,4984
1,58	0,4429	1,88	0,4699	2,36	0,4909	2,96	0,4985
1,59	0,4441	1,89	0,4706	2,38	0,4913	2,98	0,4986
1,60	0,4452	1,90	0,4713	2,40	0,4918	3,00	0,49865
1,61	0,4463	1,91	0,4719	2,42	0,4922	3,20	0,49931
1,62	0,4474	1,92	0,4726	2,44	0,4927	3,40	0,49966
1,63	0,4484	1,93	0,4732	2,46	0,4931	3,60	0,499841
1,64	0,4495	1,94	0,4738	2,48	0,4934	3,80	0,499928
1,65	0,4505	1,95	0,4744	2,50	0,4938	4,00	0,499968
1,66	0,4515	1,96	0,4750	2,52	0,4941	4,50	0,499997
1,67	0,4525	1,97	0,4756	2,54	0,4945	5,00	0,499997
1,68	0,4535	1,98	0,4761	2,56	0,4948	x>5	0,5
1,69	0,4545	1,99	0,4767	2,58	0,4951

77