§4. Простейший поток событий.

Потоком событий называют последовательность событий, которые наступают один за другим в случайные моменты времени.

Вероятность появления k событий простейшего потока за время t определяется формулой Пуассона

,

где - интенсивность потока - среднее число событий простейшего потока, происшедших за единицу времени.

№ 93. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту равно двум. Найти вероятность того, что за две минуты поступит: а) три вызова; б) менее трех вызовов; в) более трех вызовов.

Решение. По условию задачи , т.е. .

а) Тогда

.

б) Пусть , тогда

.

в) Пусть , тогда

.

Ответ: а) 0,1954; б) 0,2381; в) 0,5665.

№ 94. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно 2. Найти вероятность того, что за 3 часа поступит: а) от одной до шести заявок; б) не менее семи заявок.

№ 95. Анализ информации об индексе FTSE 100 показывает, что на протяжении последних нескольких лет, среднее число ежедневных изменений индекса более, чем на 1%, за каждый шестимесячный период равно 5. Найти вероятность того, что в течение следующих шести месяцев произойдет, по крайней мере, три дневных изменения индекса FTSE 100 на 1% и более.

Формула Пуассона применяется и для решения различных задач массового обслуживания, в которых поток требований является простейшим (пуассоновским).

Рассмотрим применение теории массового обслуживания в задачах маркетинга на примере, так называемых, разомкнутых систем массового обслуживания (СМО), в которых длина очереди поступления требований является неограниченной. Примерами таких СМО могут служить магазины, кассы вокзалов, порты и так далее.

При изучении таких систем рассчитывают различные показатели эффективности обслуживающей системы. Рассмотрим наиболее основные показатели.

Пусть n – количество каналов; - среднее число требований, поступающих в систему за единицу времени; - параметр экспоненциального закона времени обслуживания требований в системе, то есть величина, обратная среднему времени обслуживания одного требования.

Тогда можно определить следующие показатели эффективности

1. Вероятность того, что все обслуживающие каналы свободны:

.

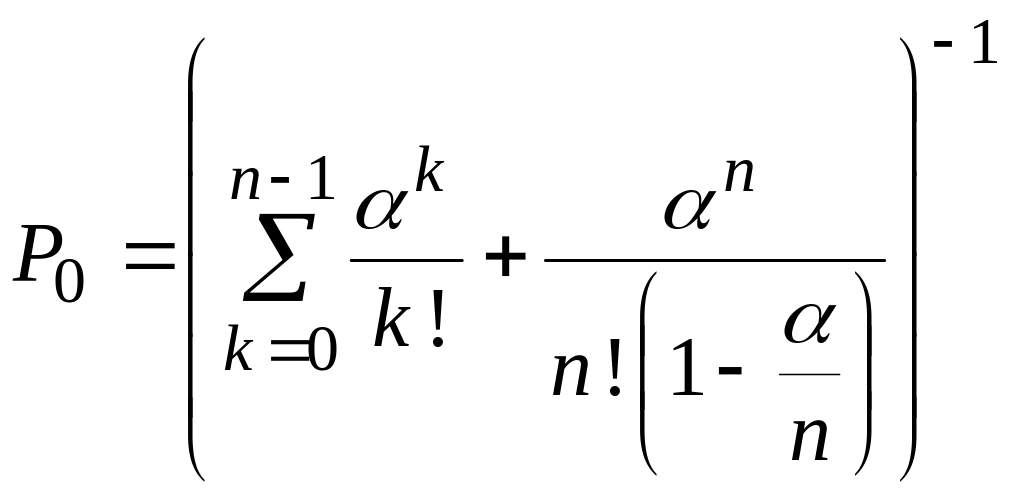2. Вероятность того, что занято ровно 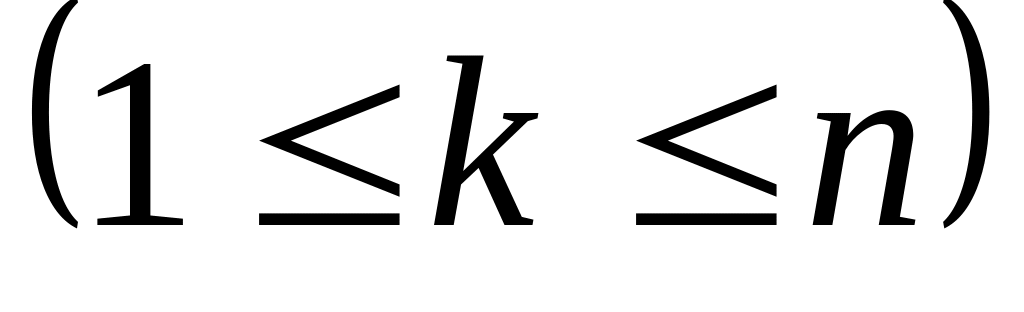обслуживающих каналов:

.

3. Вероятность того, что все обслуживающие каналы заняты:

.

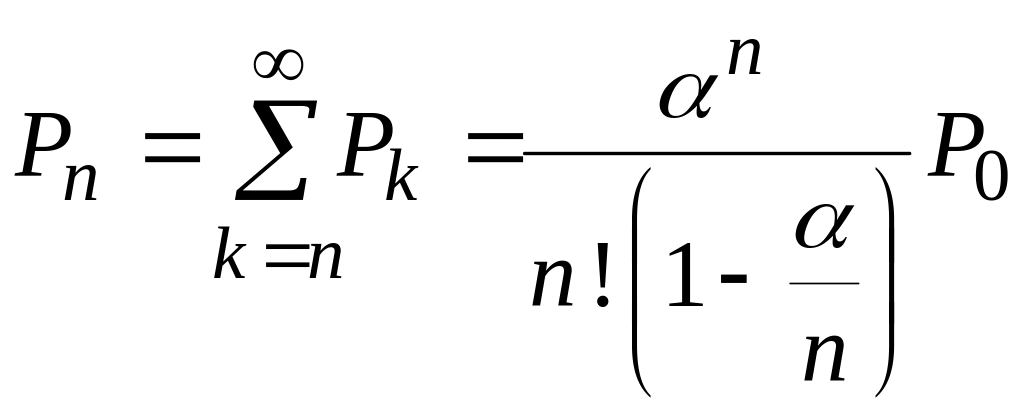4. Среднее время ожидания требованием начала обслуживания в системе:

.

5. Средняя длина очереди:

.

6. Среднее число свободных от обслуживания каналов:

.

Кроме того можно определить и такие показатели, как -коэффициент простоя каналов; коэффициент загрузки каналов , и так далее.

№ 96. Пусть фирма по ремонту теле-радио аппаратуры имеет 5 опытных мастеров. В среднем в течение рабочего дня от населения поступает на ремонт 10 аппаратов. Статистика показывает, что в среднем в течение рабочего дня каждый из мастеров успевает отремонтировать 2,5 аппарата. Оцените характеристики работы фирмы, считая, что поток заявок на ремонт аппаратуры от населения является простейшим.

Решение. Так как , , то:

1. Определим параметр системы :

.

Так как , то очередь не может расти бесконечно, то есть фирма справляется с входящим потоком требований на ремонт аппаратуры.

2. Определим вероятность того, что все мастера свободны от ремонта аппаратуры:

.

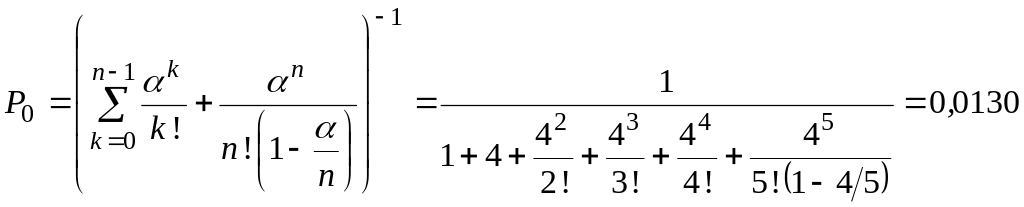Это означает, что 1,30% времени все 5 мастеров свободны от ремонта аппаратуры.

3. Определим вероятность того, что все мастера заняты ремонтом:

.

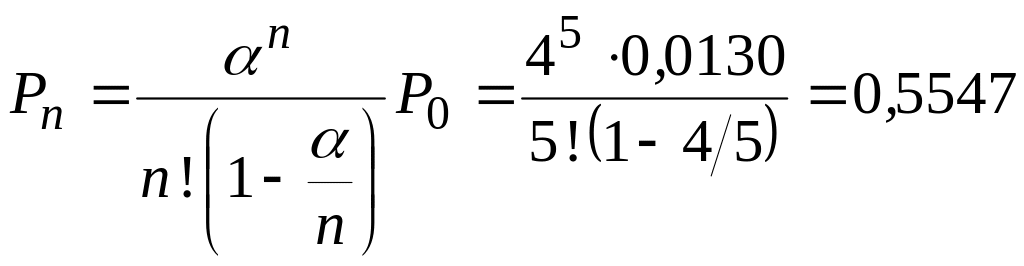Это означает, что 55,47% времени мастера полностью загружены работой.

4. Найдем среднее время ремонта каждым мастером одного аппарата, считая, что продолжительность рабочего дня равна 8 часам:

ч.

5. Определим среднее время ожидания каждым неисправным аппаратом начала ремонта:

ч.

6. Найдем среднюю длину очереди, которая определяет количество места, необходимого для хранения аппаратуры, требующей ремонта:

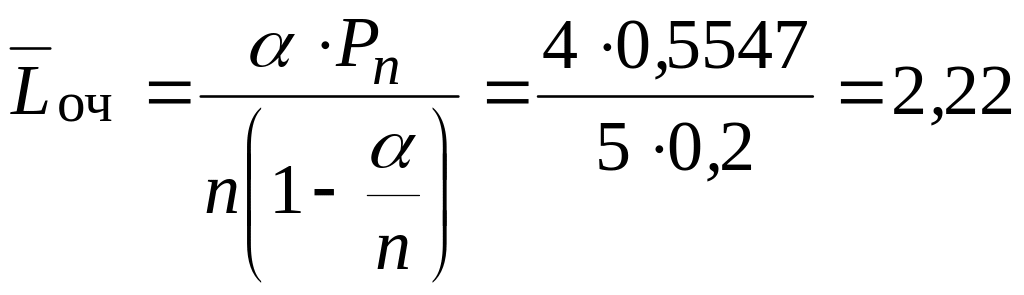аппарата.

7. Определим среднее число мастеров, свободных от работы:

мастера.

8. Можно найти также вероятность того, что будут заняты ремонтом, например, ровно 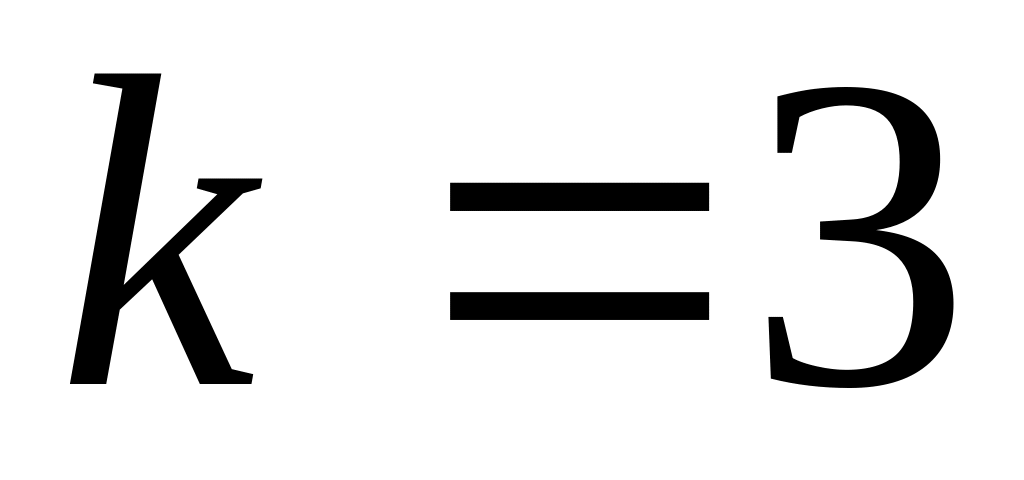мастера из мастеров:

.

Это означает, что два мастера из пяти будут свободны от ремонта аппаратуры 13,87% времени.

№ 97. В порту имеется три причала для разгрузки грузовых судов. Интенсивность потока судов равна 1,4 судна в сутки. Среднее время разгрузки судов составляет двое суток. Оцените характеристики работы порта.

№ 98. На автозаправочной станции установлены четыре колонки для выдачи бензина. На станцию прибывают в среднем 0,8 машины в минуту. Среднее время заправки одной машины составляет 3 минуты. Оцените характеристики работы заправочной станции.

Формула Пуассона наряду с задачей повторения испытаний и простейшего потока используется также для расчета вероятностей появления различного числа событий в какой-либо области (площади, объеме и т.д.). В этом случае заменяют на , где  - среднее число появлений события за какую-либо единицу области (площади, объема и т.д.), а S - размер области (площади, объема и т.д.).

№ 99. При определении зараженности зерна установлено, что в 1 кг содержится в среднем 10 вредителей. Какова вероятность того, что в 100 г зерна: а) не встретится ни одного вредителя; б) встретится не менее двух вредителей.

Г Л А В А III

Н Е П Р Е Р Ы В Н Ы Е С Л У Ч А Й Н Ы Е В Е Л И Ч И Н Ы