§ 7. Классическая задача управления запасами
В качестве приложения законов распределения случайных величин, рассмотрим задачу управления запасами товара на складе в, так называемой, классической форме, выбрав в качестве единичного интервала времени один день. Издержки склада за данный день можно записать в виде
где
- запас товара в начале дня
,
-
спрос на товар в течение этого дня,
-
стоимость издержек хранения единицы
товара,
- стоимость штрафных санкций за
недопоставку единицы товара,
- запас товара в конце дня
.
Полные
издержки (за весь период
работы склада) будут равны:
.
Предположим, что спрос является
непрерывной случайной величиной
,
с плотностью распределения
и функцией распределения вероятностей
.
Тогда полные издержки будут вычисляться
как математическое ожидание:
,
и задача управления запасами товара на
складе ставится следующим образом:
определить объем запаса на пополнение
товара
,
минимизирующий средние полные издержки
.
Рассмотрим решение поставленной задачи в статической постановке:
,
то есть, опускаем индекс
в записи объемов спроса и пополнения.
Тогда для нахождения минимума последнего
выражения по переменной
,
получаем уравнение, решение которого
позволяет найти то значение запаса
,
при котором средние полные издержки
достигают минимального значения, а
именно:
,
где величину называют плотностью убытков из-за неудовлетворенного спроса.
Таким образом, решение
определяет стратегию оптимального
пополнения запасов. А именно, величина
пополнения запасов
,
минимизирующая средние полные издержки,
задается следующим образом:
Если же спрос представляет собой
дискретную случайную величину
с вероятностями
,
,
то затраты будут минимальны при таком
запасе
,
при котором справедливо неравенство:
.
В качестве примера непрерывного закона распределения вероятностей случайного спроса рассмотрим, так называемое “треугольное” распределение, которое можно считать “приближением” нормального распределения:
Тогда оптимальный запас можно легко вычислить по формуле:
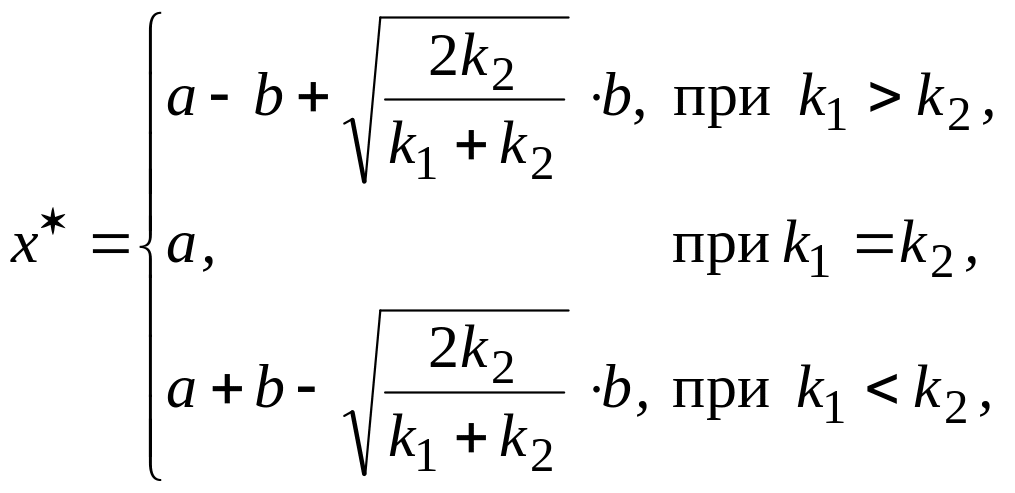
а значение минимума средних полных издержек вычисляется как:
№ 122. Предприятие закупает агрегат
с запасными блоками к нему. Стоимость
одного блока равна 500 руб. В случае выхода
агрегата из строя из-за поломки блока,
отсутствующего в запасе, простой агрегата
и срочный заказ нового блока к нему
обойдется в 5000 руб. Необходимо определить
оптимальное число запасных блоков,
которое необходимо приобрести вместе
с агрегатом, если закон распределения
вероятностей числа блоков
,
которые могут выйти из строя, имеет вид:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
0,57 |
0,24 |
0,10 |
0,06 |
0,02 |
0,009 |
0,001 |
№ 123. Решить задачу № 122, если
закон распределения вероятностей числа
блоков, которые могут выйти из строя,
подчиняется показательному распределению
при: а)
;
б)
;
в)
.
№ 124. Некоторая фирма в соответствии с договором реализует со склада по заявкам холодильники, причем ежедневный спрос является величиной случайной и колеблется от 60 до 90 холодильников в день. Средние издержки хранения одного холодильника в день составляют 200 руб., а штраф за недопоставку одного холодильника в день равен 1000 руб. Определить стратегию оптимального пополнения запаса холодильников и минимальные средние полные издержки.