
- •В.А.Кудинов, э.М.Карташов гидрАвЛика
- •Глава 1 введение
- •§ 1.1. Краткий исторический обзор развития гидравлики
- •§ 1.2. Определение науки «Гидромеханика»
- •§ 1.3. Реальные и идеальные жидкости
- •§ 1.4. Размерности физических величин, применяемых в гидРомеханИке
- •Глава 2 свойства жидкостей
- •§ 2.1. Основные физико-механические свойства жидкости
- •§ 2.2. Вязкость. Закон ньютона для внутреннего трения в жидкости
- •§ 2.3. Зависимость вязкости от температуры и давления. Вискозиметры
- •Глава 3 гидростатика
- •§ 3.1. Силы, действующие в жидкости
- •§ 3.2. Гидростатическое давление и его свойства
- •§ 3.3. Дифференциальные уравнения равновесия жидкости
- •§ 3.4. Потенциал массовых сил
- •§ 3.5. Интеграл уравнений эйлера для несжимаемой жидкости
- •§ 3.6. Уравнение поверхности равного давления
- •§ 3.7. Основное уравнение гидростатики
- •§ 3.8. Методы и приборы для измерения давления. Абсолютное и избыточное давление. Вакуум
- •§ 3.9. Гидростатический напор и энергетический закон для жидкости, находящейся в равновесии
- •§ 3.10 Интегрирование уравнений эйлера для случая относительного покоя жидкости
- •§ 3.11. Сила давления жидкости на криволинейную поверхность произвольной формы
- •§ 3.12. Частные случаи расчета сил, действующих на криволинейные поверхности закономерных форм
- •§ 3.13. Сила давления жидкости на плоскую стенку произвольной формы
- •§ 3.14. Гидростатический парадокс
- •§ 3.15. Центр давления и определение его координат
- •§ 3.16. Простые гидравлические машины. Гидравлический пресс
- •§ 3.17. Гидравлический аккумулятор
- •§ 3.18. Закон Архимеда
- •§ 3.19. Условия плавучести и остойчивости тел, частично погруженных в жидкость
- •Глава 4 Гидродинамика
- •§ 4.1. Основные кинематические понятия и определения. Два метода исследования движения жидкости
- •§ 4.2. Траектории частиц и линии тока
- •§ 4.3. Установившееся движение
- •§ 4.4. Струйчатая модель движения жидкости. Трубка тока. Расход жидкости
- •§ 4.5. Средняя скорость
- •§ 4.6. Уравнение неразрывности в переменных эйлера в декартовой системе координат
- •§ 4.7. Дифференциальные уравнения движения идеальной (невязкой) жидкости (уравнения эйлера)
- •§ 4.8. Дифференциальные уравнения движения вязкой жидкости (уравнения навье-стокса)
- •§ 4.9. Уравнение бернулли для элементарной струйки идеальной жидкости
- •§ 4.10. Физический и геометрический смысл уравнения бернулли. Напор жидкости
- •§ 4.11. Уравнение бернулли для элементарной струйки реальной жидкости
- •§ 4.12. Уравнение бернулли для потока реальной жидкости
- •§ 4.13. ГрафИческая иллюстрация уравнения бернулли для потока реальной жидкости
- •§ 4.14. Практическое применение уравнения бернулли
- •§ 4.15. Трубка прандтля
- •§ 4.16. Трубка вентури, сопло, диафрагма
- •Глава 5 основы теории гидродинамического подобия
- •§ 5.1. Основные понятия и определения теории подобия
- •§ 5.2. Теоремы теории подобия. Критерии подобия
- •§ 5.3. Физический смысл критериев подобия
- •§5.4. Метод анализа размерности
- •Глава 6
- •§ 6.1. Два режима движения жидкости
- •§ 6.2. Равномерное движение жидкости
- •§ 6.3. Основное уравнение равномерного потока. Уравнение динамического равновесия равномерного потока
- •§ 6.4. Ламинарное движение жидкости
- •§ 6.5. Расход жидкости
- •§ 6.6. Коэффициент линейных потерь при ламинарном движении жидкости
- •§ 6.7. Формирование изотермического ламинарного потока
- •§ 6.8. Основы гидродинамической теории смазки
- •§ 6.9. Турбулентное движение жидкости
- •§ 6.10. Турбулентное перемешивание. Пульсация скоростей и напряжений при турбулентном режиме
- •§ 6.11. Осреднение скоростей
- •§ 6.12. Осреднение напряжений
- •§ 6.13. Структура турбулентного потока
- •§ 6.14. Касательные напряжения в турбулентном потоке
- •§ 6.15. Полуэмпирические теории турбулентности
- •§ 6.16. Логарифмический закон распределения скоростей в круглой трубе
- •§ 6.17. Экспериментальные данные для коэффициента гидравлического сопротивления. Опыты Никурадзе и Зегжда
- •§ 6.18. Формулы для определения коэффициента гидравлического сопротивления
- •§ 6.19. Местные сопротивления
- •§ 6.20. Зависимость коэффициента местных потерь от числа Рейнольдса
- •§ 6.21. Принцип наложения потерь напора. Коэффициент сопротивления системы
- •§ 6.22. Основные расчетные формулы для определения потерь напора
- •Глава 7 Гидравлический расчёт трубопроводов
- •§ 7.1. Назначение и классификация трубопроводов
- •§ 7.2. Расчет и проектирование трубопроводов
- •§ 7.3. Гидравлический расчет простого трубопровода
- •§ 7.4. Метод эквивалентных потерь
- •§ 7.5. Гидравлический расчет сложных трубопроводов
- •§ 7.6. Гидравлические характеристики трубопроводов
- •§ 7.7. Гидроэнергетический баланс насосной установки
- •§ 7.8. Сифонные трубопроводы
- •§ 7.9. Гидравлический удар в трубах
- •§ 7.10. Кавитация
- •Глава 8 Истечение жидкости через отверстия и насадки
- •§ 8.1. Истечение через малое отверстие в тонкой стенке
- •§ 8.2. Истечение через большое отверстие
- •§ 8.3. Истечение через затопленное отверстие
- •§ 8.4. Истечение жидкости при переменном напоре
- •§ 8.5. Истечение через насадки
- •Оглавление
- •Средние значения модуля упругости е жидких и твердых тел
- •Средние значения эквивалентной шероховатости э
- •Библиографический список
§ 6.2. Равномерное движение жидкости
Равномерным потоком жидкости называется
такой поток, в котором все частицы
движутся равномерно и прямолинейно. В
таком потоке все живые сечения будут
плоскими и распределения скоростей по
сечениям одинаковыми, т.е.
![]() (рис.6.4).
(рис.6.4).
В равномерном потоке
![]() ,
,
![]() ,
,
![]() ,
,
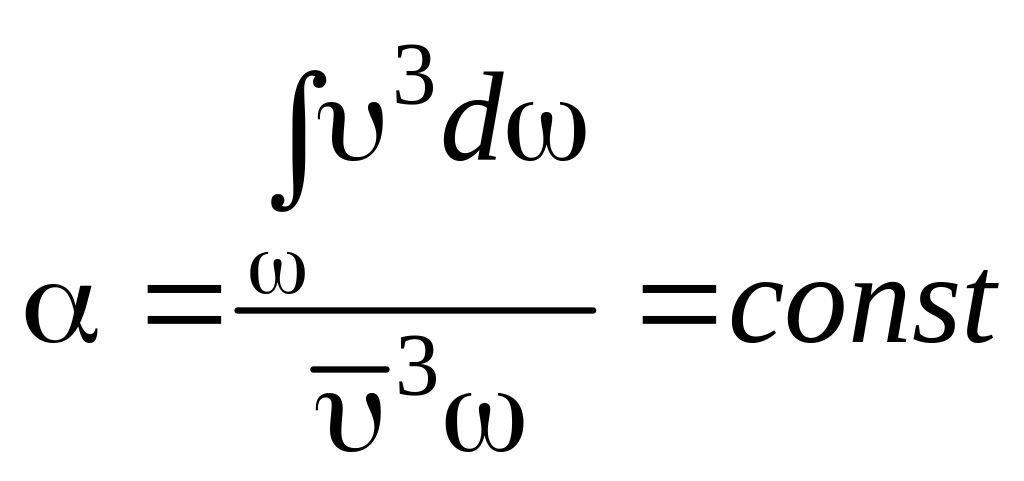 .
.
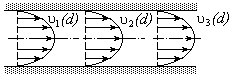
Рис. 6.4
Так как равномерное движение есть предельный случай плавноизменяющегося, то ясно, что давление в живых сечениях потока при равномерном движении будет меняться по гидростатическому закону, т.е.
![]() .
.
Удельная кинетическая энергия при равномерном движении
![]() ,
,
так как
![]() и
и
![]() ,
т.е. удельная кинетическая энергия во
всех живых сечениях потока одинакова.
Следовательно, вдоль равномерного
потока уменьшается лишь потенциальная
энергия, расходуемая на потери.
,
т.е. удельная кинетическая энергия во
всех живых сечениях потока одинакова.
Следовательно, вдоль равномерного
потока уменьшается лишь потенциальная
энергия, расходуемая на потери.
Так как все частицы жидкости в данном сечении обладают одинаковыми запасами удельной потенциальной энергии, то потеря энергии на любой линии тока между двумя сечениями одна и та же. Отсюда следует важный вывод, что в равномерном потоке гидравлический уклон
![]() ,
,
т.е. не зависит от расположения частицы от оси потока.
§ 6.3. Основное уравнение равномерного потока. Уравнение динамического равновесия равномерного потока
Проведем исследование равномерного потока с целью вывода основных уравнений, характеризующих его. При равномерном движении средние скорости во всех поперечных сечениях одинаковы, местные сопротивления отсутствуют и существуют лишь сопротивления трения, проявляющиеся по длине трубопровода и вызывающие соответствующие потери напора.
Выведем сначала уравнение динамического равновесия. Для этого рассмотрим равномерный поток жидкости в цилиндрической трубе (рис.6.5.).
Выделим в потоке отсек длиной l с площадью поперечного сечения . Контур, ограничивающий площадку , обозначим через (хи). обычно называют смоченным периметром. Контур выберем концентрично по отношению к стенкам трубы.
На выделенный отсек действуют следующие силы.
1. Сила тяжести
G = γωl.
2. Силы гидродинамического давления
![]() ;
;![]() ,
,
где p1 и p2- давления в соответствующих сечениях жидкости. (Поскольку в равномерном потоке гидромеханические давления распределяются в сечении по линейному закону, то в этих формулах под p1 и p2 cледует понимать давления, действующие в центре тяжести площадок 1 и 2 ).
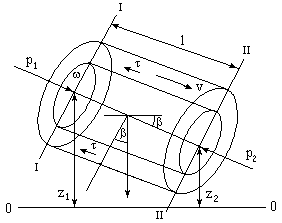
Рис.6.5
3. Силы трения
![]() ,
где (l)
- боковая поверхность выделенного
отсека.
,
где (l)
- боковая поверхность выделенного
отсека.
Составим уравнение движения на направление l. Так как силы инерции в равномерном потоке отсутствуют, то получим
F1 – F2 – T + G sinβ = 0
или
![]() .
.
Так как
![]() ,то
,то
![]() .
.
Поделив обе части уравнения на
и и учитывая, что
![]() ,
находим
,
находим
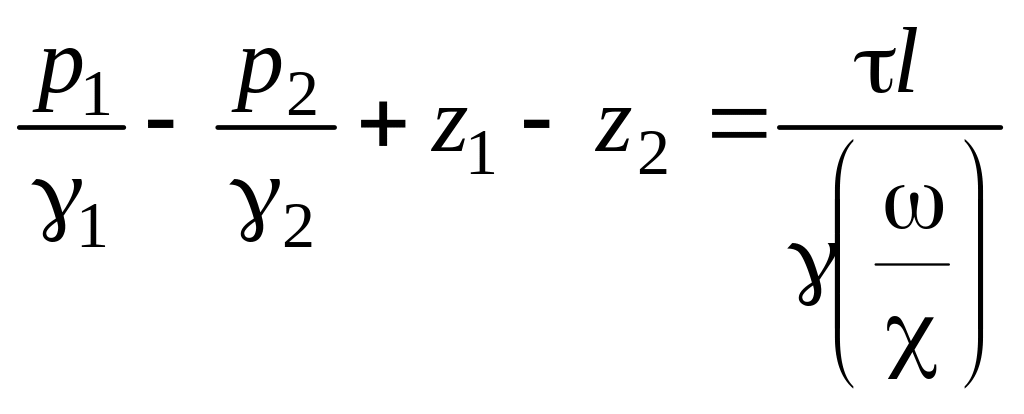 .
.
Обозначив
![]() ,
где R - гидравлический
радиус, будем иметь
,
где R - гидравлический
радиус, будем иметь
![]() .
(6.1)
.
(6.1)
Соотношение (6.1) представляет уравнение динамического равновесия равномерного потока.
Выведем уравнение энергии равномерного потока. Уравнение Бернулли для потока имеет вид
![]() .
.
В равномерном потоке 1
= 2 и
![]() и, следовательно,
и, следовательно,
![]() .
.
Тогда
![]() .
(6.2)
.
(6.2)
Объединяя (6.1) и (6.2), получим общее выражение для потери напора по длине потока
![]() .
.
Последнее уравнение называют основным уравнением равномерного потока. Этому уравнению можно придать несколько иной вид
![]() .
.
Отсюда
![]()
или
![]() ,
,
где J - гидравлический уклон потока. Последние два соотношения также представляют основное уравнение равномерного потока.
Для касательного напряжения на стенке это уравнение принимает вид
![]()
или
![]() .
.
Уравнение равномерного потока показывает, что напряжение силы трения, отнесенное к удельному весу жидкости, равно произведению гидравлического радиуса на гидравлический уклон.
