§ 3.9. Гидростатический напор и энергетический закон для жидкости, находящейся в равновесии

При выводе основного уравнения гидростатики выше (см. п. 3.7) было получено дифференциальное уравнение вида

.

Прежде чем интегрировать это уравнение, представим его в следующем виде

или

.

Проинтегрировав, получим

.

Величина представляет ту высоту, на которую поднялась бы жидкость в пьезометре, если бы верхний конец его находился под нулевым давлением p = 0 (рис. 3.12).

Таким образом, это есть высота, соответствующая абсолютному давлению в жидкости. Она называется приведенной (высота h₂).

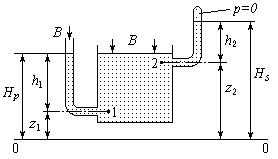
Рис. 3.12

- геометрическая высота выбранной точки над условной плоскостью сравнения 0 - 0. Отсюда

. (3.24)

Уравнение (3.24) показывает, что сумма двух высот и для любой точки жидкости остается постоянной. Эта сумма называется абсолютным (полным) гидростатическим напором.

Если конец пьезометра соединить с атмосферой при давлении B, то уравнение (3.24) примет вид

. (3.25)

Сумма и называется гидростатическим напором, а величина - пьезометрическим напором.

Горизонтальная плоскость, проведенная на высоте , называется плоскостью гидростатического или пьезометрического напора, а - плоскостью абсолютного (полного) напора. Очевидно, что .

Выражениям (3.24) и (3.25) можно придать простой энергетический смысл. Рассмотрим частицу жидкости массой m. Ее потенциальная энергия относительно плоскости 0 - 0 будет mgz. Кроме того, под действием давления p частица может подняться на высоту , т.е. обладает потенциальной энергией давления, равной

.

Таким образом, полный запас потенциальной энергии частицы будет

.

Разделив последнее соотношение на mg, получим

,

где .

Отсюда следует, что высота z - есть удельная потенциальная энергия положения частицы, а - удельная потенциальная энергия давления.

Величина

является полной удельной потенциальной энергией частицы.

Последнее соотношение называется энергетическим законом для жидкости, находящейся в равновесии.

Для всех точек данного объема покоящейся жидкости удельная потенциальная энергия одинакова. Эти утверждения справедливы как для полного , так и для пьезометрического напоров.

§ 3.10 Интегрирование уравнений эйлера для случая относительного покоя жидкости

Пусть жидкость находится в емкости, которая движется прямолинейно и равноускоренно по горизонтальной плоскости с ускорением а (рис. 3.13).

Масса жидкости при движении находится под действием массовой силы тяжести и силы инерции от горизонтального перемещения. Соответствующие проекции массовых сил будут равны .

Уравнение (3.15), учитывая массовые силы, примет вид

.

Переменные в уравнении разделены. Интегрируя его, получим

, (3.26)

где C - постоянная интегрирования, определяемая из граничных условий, которые в данном случае имеют вид при x=0 и z=0.

Отсюда

. (3.27)

Подставляя (3.27) в (3.26), найдем

. (3.28)

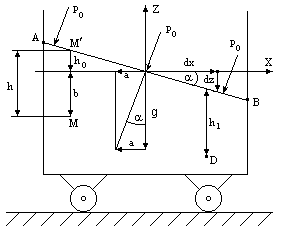
Рис. 3.13

Уравнение (3.28) для свободной поверхности, где p = p₀, примет вид

.

Отсюда

. (3.29)

Так как a/g является константой, то уравнение (3.29) будет уравнением прямой линии. Это означает, что плоскость, проведенная через оси x и z , будет пересекать наружную поверхность жидкости по линии AB.

Отношение a/g представляет тангенс угла наклона прямой AB к горизонтальной плоскости .

Отсюда .

Запишем уравнение (3.28) для некоторой точки M в виде

или

. (3.30)

Согласно (3.29) первый член в правой части уравнения (3.30) будет ,так как точка M находится на поверхности.

Отсюда, учитывая, что , а получим

или

. (3.31)

Уравнение (3.31) представляет формулу гидростатического давления (3.23). Таким образом, давление в любой точке жидкости, движущейся вместе с емкостью прямолинейно и равноускоренно, определяется по формуле гидростатического давления, где h - глубина погружения точки под поверхностью жидкости. Например, давление в точке D будет .

Рассмотрим теперь жидкость, находящуюся в цилиндрической емкости, которая вращается вокруг вертикальной оси с постоянной угловой скоростью  (рис. 3.14 ).

Ц

Рис. 3.14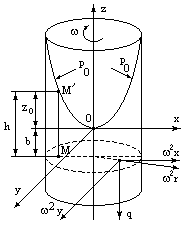

ентробежная сила на единицу массы

,

где V -окружная скорость.

Проекции массовых сил на соответствующие оси координат будут

;

;

.

Подставляя их значения в соотношение

,

получим

.

Интегрируя, найдем

,

где C - постоянная интегрирования. Так как при x = 0, y = 0, z = 0 p = p_0, то C = p₀. Учитывая, что , находим

(3.32)

По формуле (3.32) можно найти давление в любой точке М жидкости по глубине емкости. Для нахождения поверхностей равного давления положим dp=0, тогда будем иметь

.

Интегрируя, получим

.

Отсюда

.

Следовательно, поверхности равного давления представляют собой параболоиды вращения.

При r = 0, z = 0 получаем C = 0 для уравнения свободной поверхности. Тогда уравнение свободной поверхности

.

Найдем давление в некоторой точке М, расположенной на глубине h от поверхности. Обозначив аппликату свободной поверхности через z₀ (точка М), получим

.

Подставляя это выражение в (3.32), находим

или

,

где . Таким образом, вновь получили формулу гидростатического давления.