§ 5.2. Теоремы теории подобия. Критерии подобия
Очевидно,
что подобные явления должны принадлежать
лишь к одному классу, т.е. описываться
одной и той же системой дифференциальных
уравнений. В общем случае дифференциальные
уравнения не могут соблюдаться
одновременно при переменных x,
и т.д. и при новых переменных
,
и т.д. То есть в общем случае дифференциальные
уравнения и уравнения группового
преобразования несовместны.
Покажем, что для того чтобы переменные одновременно удовлетворяли дифференциальным уравнениям и уравнениям группового преобразования, множители Cl, C и т.д. не могут выбираться произвольно, а связаны определенными соотношениями.
Выпишем одно из уравнений Навье-Стокса для 1-го явления (образца)
(5.4)
Для 2-го явления (модели), подобного 1-му, положим
;
;
;
;
;
;
;
;
.
(5.5)
Уравнение Навье-Стокса для модели будет
(5.6)
Подставляя (5.5) в (5.6) и учитывая, что константы подобия С постоянны и при дифференцировании выносятся за знак дифференциала, получим
.
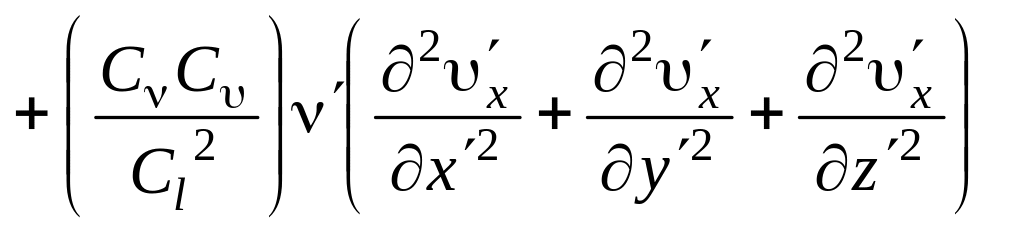(5.7)
Из соотношения (5.7) можно заключить, что для совместности уравнений (5.4) и (5.6), т.е. для того чтобы переменные 1-го и 2-го явлений удовлетворяли бы одному и тому же дифференциальному уравнению, должно быть
.
Или, разделив все на
,
получим
.
Отсюда
.
Учитывая, что из (5.5)
и т.д., получим
или
.
То есть комплекс величин в соответствующих точках образца и модели должен быть неизменен (условие равенства чисел подобия обозначается значком idem)
или
;
или
;
или
.
Величины Ho, Fr, Eu, Re носят название критериев подобия.
Ho - критерий гомохронности;
Fr - критерий Фруда;
Eu - критерий Эйлера;
Re - критерий Рейнольдса.
Первая теорема подобия (теорема Ньютона) при этом будет: у подобных явлений для любой пары соответственных точек критерии подобия численно одинаковы. При переходе от одной пары соответственных точек к другой критерии подобия изменяют значение. Эта теорема дает необходимые условия подобия.
Рассмотрим теперь условия, которые достаточны для того чтобы явления в модели и образце были подобны. Понятие подобия распространяется на все соответственные точки подобных систем, в том числе и на границах систем, а также и в начальный момент времени. Но отдельные явления различаются между собой лишь условиями однозначности. Поэтому, если условия однозначности сделать подобными, то и сами явления окажутся подобными, если они описываются одними и теми же дифференциальными уравнениями. Но для подобия условий однозначности достаточно соблюсти равенство критериев подобия, составленных лишь из величин, входящих в условия однозначности. Поэтому можно сказать: подобны те явления, условия однозначности которых подобны, а критерии подобия, составленные из величин, входящих в условия однозначности, равны. Это утверждение составляет 3-ю теорему подобия (теорему Кирпичева-Гухмана).
Значение этой теоремы состоит в том,
что она позволяет воспроизводить
подобные явления, т.е. моделировать их.
Согласно этой теореме для того чтобы
модель была подобна образцу, достаточно
осуществить пропорциональность всех
величин на границе явления и в начальный
момент времени, выбрав эти величины
так, чтобы критерии, составленные из
них, были численно равны для соответствующих
точек модели и образца. Например, при
течении жидкости в гладкой круглой
трубе в условия однозначности входят
.
Поэтому должно быть
или
.
Отсюда
.
Если
и
,
то на входе должно быть
.
Именно в этом случае условия однозначности
будут подобны.
Все критерии, полученные из данной системы уравнений, можно разбить на 2 категории. К первой категории относятся критерии, составленные из величин, входящих в условия однозначности. Эти критерии называются определяющими, так как они определяют достаточные условия подобия. Ко второй категории относятся все остальные критерии, получающиеся из системы уравнений. Они называются неопределяющими.
Если значения определяющих критериев у 2-х явлений в соответственных точках равны, то явления подобны. Но если они подобны, то по 1-й теореме подобия они имеют в соответственных точках одинаковые значения всех критериев, независимо от того, к которой из 2-х категорий они относятся. Отсюда следует, что равенство определяющих критериев имеет следствием равенство всех остальных критериев. А это означает существование функциональной зависимости между определяющими и неопределяющими критериями.
В самом деле, если мы перейдем от одних
значений определяющих критериев к
другим, то мы перейдем от одной группы
подобных явлений к другой. Но при этом
и все остальные неопределяющие критерии
получат какие-то новые единственные
значения. Таким образом, каждый
неопределяющий критерий есть однозначная
функция определяющих критериев.
Например,
.
Вид этой функции может быть найден из
опыта. Если мы получим из опыта зависимость
и построим эту зависимость в виде
графика, то каждая точка на таком графике
будет отвечать целой группе подобных
явлений, для которых
,
а вся кривая в целом - серии групп.
Между тем одна точка на графике может
быть получена в результате единичного
опыта, а вся кривая в виде небольшой
серии опытов на единственной установке.
Например, после того как найдено число
,
перепад Δp находится
по формуле
.
Таким образом, мы можем обобщить результаты единичного эксперимента на целую серию групп и получить решение или интеграл дифференциального уравнения в виде критериального уравнения. Отсюда вторая теорема подобия (теорема Федермана-Букингема) формулируется следующим образом: решение системы дифференциальных уравнений может быть представлено в виде функции между критериями подобия этой системы.
Значение 2-й теоремы подобия состоит в том, что она позволяет не интегрировать систему дифференциальных уравнений, а получать ее интеграл из опыта в виде критериального уравнения. Кроме того, она указывает на то, что данные опыта должны обрабатываться в виде функциональной зависимости между критериями подобия.