§ 4.16. Трубка вентури, сопло, диафрагма
В промышленных условиях для измерения расхода жидкостей применяются трубки Вентури, сопла и диафрагмы. Более подробно рассмотрим трубку Вентури (рис. 4.25). Трубка Вентури создает в трубопроводе местное сужение потока и по возникающему перепаду давлений p можно определить расход жидкости.
Для сечений I и II запишем уравнение Бернулли (считая распределение скоростей равномерным)
,
где hM
- потеря напора между сечениями I и II,
;
- коэффициент
местных потерь (см. § 6.21).
Уравнение неразрывности для несжимаемой жидкости имеет вид
.
Отсюда
.
Подставляя hM,
1,
и
в уравнение Бернулли и выражая 2,
получим
.
Объемный расход будет определяться по формуле
Рис. 4.25 |
Рис. 4.26
|
,
(4.19)
где C - величина, постоянная для данного расходомера (трубки Вентури).
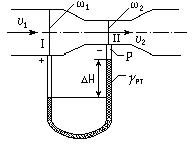
Довольно часто вместо пьезометров 1 и 2 для измерения перепада давления в расходомере применяют дифференциальный трубный манометр (рис. 4.26).
Рис. 4.27 Рис. 4.28
Учитывая, что над ртутью в трубках находится одна и та же жидкость плотностью , можно записать (см. рис. 4.26)
.
(4.20)
Значения
,
полученные по формуле (4.20), можно
использовать для определения расхода
по формуле (4.19).
Аналогично для измерения расхода могут быть использованы диафрагмы (рис. 4.27) и сопла (рис. 4.28).
Задача 1. При ламинарном режиме
движения жидкости по горизонтальному
трубопроводу диаметром
расход жидкости равен
(рис. 4.29). Падение пьезометрической
высоты на участке длиной
составляет
.
Определить коэффициенты кинематической
и динамической
вязкости жидкости. Исходные данные
задачи:
;
;
;
;
.
Рис. 4.29
Решение.
; 
; 
; 
;
.
(а)
Запишем уравнение Бернулли для сечений 1 и 2 трубы
.
Так как
и
,
то уравнение Бернулли примет вид
,
где
; 
.
Учитывая, что
,
получим
.
Отсюда
.
Известно, что λ = 64/ Re – формула Пуазейля. Отсюда Re = 64/λ.
Подставляя последнее соотношение в (а), получим
.
Отсюда
.
Учитывая, что
м2,
получим
.
Так как
,
то
.
Глава 5 основы теории гидродинамического подобия
Существует два метода исследования физических явлений – аналитический и экспериментальный. При аналитическом исследовании движения жидкости задача сводится к интегрированию сиcтемы дифференциальных уравнений при заданных условиях однозначности. Например, для вязкой несжимаемой жидкости имеем следующую сиcтему дифференциальных уравнений
;
(5.1)
,
(5.2)
где (5.1) – система уравнений Навье – Стокса, записанных в векторной форме (см. § 4.8); (5.2) - уравнение неразрывности. Кроме того, должны быть заданы начальные и граничные условия и значения физических постоянных и .
В принципе, совокупностью системы основных дифференциальных уравнений и условий однозначности конкретное единичное явление определено вполне. Однако эти уравнения чрезвычайно сложны (являются уравнениями в частных производных) и решения найдены лишь для небольшого числа частных случаев, к тому же при весьма существенных упрощающих предпосылках.
Другим методом исследования является непосредственный эксперимент. При этом измеряются те величины, которые представляют прямой практический интерес и находятся связи, допускающие непосредственное приложение. Однако данные, полученные из опыта, будут относиться только к тому частному случаю, который подвергался эксперименту. Необходимо найти пути обобщения данных опыта на другие родственные явления. Это позволило бы на основании немногих экспериментов судить о параметрах жидкости в многочисленных родственных явлениях. Задача нахождения научно обоснованного метода обобщения данных опыта решается теорией подобия, которая является учением о методах обобщения данных опыта.