
- •В.А.Кудинов, э.М.Карташов гидрАвЛика
- •Глава 1 введение
- •§ 1.1. Краткий исторический обзор развития гидравлики
- •§ 1.2. Определение науки «Гидромеханика»
- •§ 1.3. Реальные и идеальные жидкости
- •§ 1.4. Размерности физических величин, применяемых в гидРомеханИке
- •Глава 2 свойства жидкостей
- •§ 2.1. Основные физико-механические свойства жидкости
- •§ 2.2. Вязкость. Закон ньютона для внутреннего трения в жидкости
- •§ 2.3. Зависимость вязкости от температуры и давления. Вискозиметры
- •Глава 3 гидростатика
- •§ 3.1. Силы, действующие в жидкости
- •§ 3.2. Гидростатическое давление и его свойства
- •§ 3.3. Дифференциальные уравнения равновесия жидкости
- •§ 3.4. Потенциал массовых сил
- •§ 3.5. Интеграл уравнений эйлера для несжимаемой жидкости
- •§ 3.6. Уравнение поверхности равного давления
- •§ 3.7. Основное уравнение гидростатики
- •§ 3.8. Методы и приборы для измерения давления. Абсолютное и избыточное давление. Вакуум
- •§ 3.9. Гидростатический напор и энергетический закон для жидкости, находящейся в равновесии
- •§ 3.10 Интегрирование уравнений эйлера для случая относительного покоя жидкости
- •§ 3.11. Сила давления жидкости на криволинейную поверхность произвольной формы
- •§ 3.12. Частные случаи расчета сил, действующих на криволинейные поверхности закономерных форм
- •§ 3.13. Сила давления жидкости на плоскую стенку произвольной формы
- •§ 3.14. Гидростатический парадокс
- •§ 3.15. Центр давления и определение его координат
- •§ 3.16. Простые гидравлические машины. Гидравлический пресс
- •§ 3.17. Гидравлический аккумулятор
- •§ 3.18. Закон Архимеда
- •§ 3.19. Условия плавучести и остойчивости тел, частично погруженных в жидкость
- •Глава 4 Гидродинамика
- •§ 4.1. Основные кинематические понятия и определения. Два метода исследования движения жидкости
- •§ 4.2. Траектории частиц и линии тока
- •§ 4.3. Установившееся движение
- •§ 4.4. Струйчатая модель движения жидкости. Трубка тока. Расход жидкости
- •§ 4.5. Средняя скорость
- •§ 4.6. Уравнение неразрывности в переменных эйлера в декартовой системе координат
- •§ 4.7. Дифференциальные уравнения движения идеальной (невязкой) жидкости (уравнения эйлера)
- •§ 4.8. Дифференциальные уравнения движения вязкой жидкости (уравнения навье-стокса)
- •§ 4.9. Уравнение бернулли для элементарной струйки идеальной жидкости
- •§ 4.10. Физический и геометрический смысл уравнения бернулли. Напор жидкости
- •§ 4.11. Уравнение бернулли для элементарной струйки реальной жидкости
- •§ 4.12. Уравнение бернулли для потока реальной жидкости
- •§ 4.13. ГрафИческая иллюстрация уравнения бернулли для потока реальной жидкости
- •§ 4.14. Практическое применение уравнения бернулли
- •§ 4.15. Трубка прандтля
- •§ 4.16. Трубка вентури, сопло, диафрагма
- •Глава 5 основы теории гидродинамического подобия
- •§ 5.1. Основные понятия и определения теории подобия
- •§ 5.2. Теоремы теории подобия. Критерии подобия
- •§ 5.3. Физический смысл критериев подобия
- •§5.4. Метод анализа размерности
- •Глава 6
- •§ 6.1. Два режима движения жидкости
- •§ 6.2. Равномерное движение жидкости
- •§ 6.3. Основное уравнение равномерного потока. Уравнение динамического равновесия равномерного потока
- •§ 6.4. Ламинарное движение жидкости
- •§ 6.5. Расход жидкости
- •§ 6.6. Коэффициент линейных потерь при ламинарном движении жидкости
- •§ 6.7. Формирование изотермического ламинарного потока
- •§ 6.8. Основы гидродинамической теории смазки
- •§ 6.9. Турбулентное движение жидкости
- •§ 6.10. Турбулентное перемешивание. Пульсация скоростей и напряжений при турбулентном режиме
- •§ 6.11. Осреднение скоростей
- •§ 6.12. Осреднение напряжений
- •§ 6.13. Структура турбулентного потока
- •§ 6.14. Касательные напряжения в турбулентном потоке
- •§ 6.15. Полуэмпирические теории турбулентности
- •§ 6.16. Логарифмический закон распределения скоростей в круглой трубе
- •§ 6.17. Экспериментальные данные для коэффициента гидравлического сопротивления. Опыты Никурадзе и Зегжда
- •§ 6.18. Формулы для определения коэффициента гидравлического сопротивления
- •§ 6.19. Местные сопротивления
- •§ 6.20. Зависимость коэффициента местных потерь от числа Рейнольдса
- •§ 6.21. Принцип наложения потерь напора. Коэффициент сопротивления системы
- •§ 6.22. Основные расчетные формулы для определения потерь напора
- •Глава 7 Гидравлический расчёт трубопроводов
- •§ 7.1. Назначение и классификация трубопроводов
- •§ 7.2. Расчет и проектирование трубопроводов
- •§ 7.3. Гидравлический расчет простого трубопровода
- •§ 7.4. Метод эквивалентных потерь
- •§ 7.5. Гидравлический расчет сложных трубопроводов
- •§ 7.6. Гидравлические характеристики трубопроводов
- •§ 7.7. Гидроэнергетический баланс насосной установки
- •§ 7.8. Сифонные трубопроводы
- •§ 7.9. Гидравлический удар в трубах
- •§ 7.10. Кавитация
- •Глава 8 Истечение жидкости через отверстия и насадки
- •§ 8.1. Истечение через малое отверстие в тонкой стенке
- •§ 8.2. Истечение через большое отверстие
- •§ 8.3. Истечение через затопленное отверстие
- •§ 8.4. Истечение жидкости при переменном напоре
- •§ 8.5. Истечение через насадки
- •Оглавление
- •Средние значения модуля упругости е жидких и твердых тел
- •Средние значения эквивалентной шероховатости э
- •Библиографический список
§ 3.19. Условия плавучести и остойчивости тел, частично погруженных в жидкость
Наличие условия
![]() необходимо для равновесия тела,
погруженного в жидкость, но еще
недостаточно. Для равновесия тела,
кроме равенства
,
необходимо также, чтобы линии этих сил
были направлены по одной прямой, т.е.
совпадали (рис. 3.25 а).
необходимо для равновесия тела,
погруженного в жидкость, но еще
недостаточно. Для равновесия тела,
кроме равенства
,
необходимо также, чтобы линии этих сил
были направлены по одной прямой, т.е.
совпадали (рис. 3.25 а).
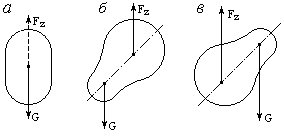
Рис. 3.25
Если тело однородно, то точки приложения указанных сил всегда совпадают и направлены по одной прямой. Если тело неоднородно, то точки приложения этих сил не совпадут и силы G и Fz образуют пару сил (см. рис. 3.25 б, в). Под действием этой пары сил тело будет вращаться в жидкости до тех пор, пока точки приложения сил G и Fz не окажутся на одной вертикали, т.е. момент пары сил будет равен нулю (рис.3.26).
Н
Рис.
3.26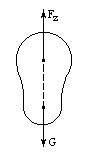
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется остойчивостью.
Рассмотрим условия, при которых плавающее на поверхности жидкости тело остойчиво.
На рис. 3.27 (а, б) C - центр тяжести (точка приложения равнодействующей сил веса G); D - точка приложения равнодействующей выталкивающих сил Fz; M - метацентр (точка пересечения равнодействующей выталкивающих сил с осью плавания 00).
Дадим некоторые определения.
Вес жидкости, вытесненной погруженным в нее телом, называется водоизмещением.
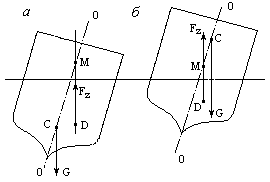
Рис. 3.27
Точка приложения равнодействующей выталкивающих сил называется центром водоизмещения (точка D).
Расстояние MC между метацентром и центром водоизмещения называется метацентрическим радиусом.
Таким образом, плавающее тело имеет три характерные точки:
1. Центр тяжести C, не меняющий своего положения при крене.
2. Центр водоизмещения D, перемещающийся при крене тела, так как очертания объема, вытесняемого в жидкости, при этом меняются.
3. Метацентр M, также изменяющий свое положение при крене.
При плавании тела могут представиться следующие 3 основных случая в зависимости от относительного расположения центра тяжести C и метацентра M.
Случай остойчивого равновесия. В этом случае метацентр лежит выше центра тяжести (рис.3.27,а) и при крене пара сил G и Fz стремится возвратить тело в первоначальное состояние (тело вращается против часовой стрелки).
Случай безразличного равновесия. В этом случае метацентр и центр тяжести совпадают и тело, выведенное из состояния равновесия, остается неподвижным.
Случай неостойчивого равновесия. Здесь метацентр лежит ниже центра тяжести (рис. 3.27,б) и образовавшаяся при крене пара сил вызывает вращение тела по часовой стрелке, что может привести к опрокидыванию плавающего средства.
Задачи
Задача 1. Паровой прямодействующий
насос подает жидкость Ж на высоту
Н (рис. 3.28). Найти рабочее давление
пара при следующих исходных
данных:![]() ;
; ![]() ;
; ![]() . Жидкость – вода (
. Жидкость – вода (![]() ).
Найти также силу, действующую на малый
и большой поршни.
).
Найти также силу, действующую на малый
и большой поршни.
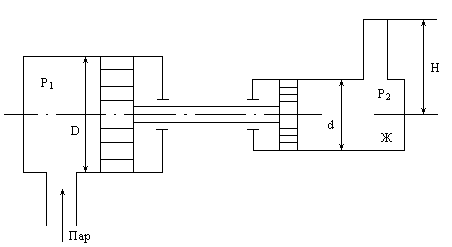
Рис. 3.28
Решение. Найдем давление
![]() на малом поршне
на малом поршне
![]() .
.
Сила
![]() ,
действующая на малый поршень, будет
,
действующая на малый поршень, будет
![]() .
.
Эта же сила действует на большой поршень, т.е.
![]() .
.
Отсюда
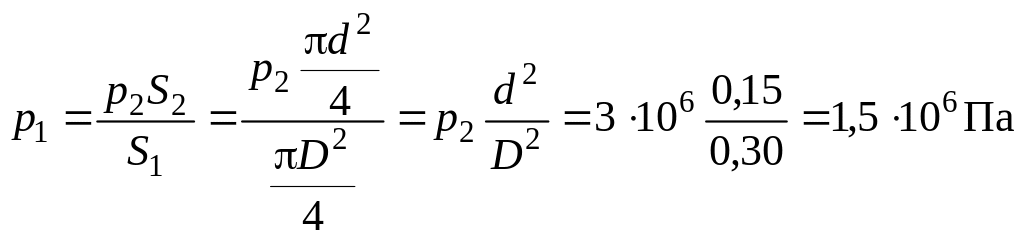 .
.
Задача 2. Определить силу
прессования
,
развиваемую гидравлическим прессом,
у которого диаметр большого поршня
![]() ,
а малого –
,
а малого –
![]() ,
при следующих исходных данных (рис.
3.29):
,
при следующих исходных данных (рис.
3.29):
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
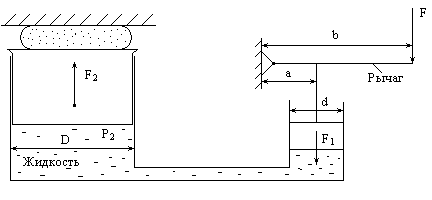
Рис. 3.29
Решение. Найдем силу
![]() ,
действующую на малый поршень. Для этого
составим условие равновесия рычага
пресса
,
действующую на малый поршень. Для этого
составим условие равновесия рычага
пресса
![]() .
.
Отсюда
![]()
Давление жидкости под малым поршнем будет
![]() ,
,
где
![]() .
.
Давление жидкости под большим поршнем
![]() ,
,
где
![]() .
.
По закону Паскаля давление в жидкости
передается по всем направлениям без
изменения. Отсюда
![]() или
или
![]() .
.
Отсюда
![]() .
.
