3.4. Теорія корисності та її основні елементи

Проблема раціонального вибору є однією з основних економічних задач. її постійно розв'язують усі суб'єкти економічних відносин: виробники намагаються найвигідніше вкласти капітал у виробництво продукції, яка приносить дохід; споживачі прагнуть придбати товари з високою споживчою цінністю за прийнятною ціною; інвестори намагаються зробити вкладення, які б підвищили вартість капіталу фірми, тощо. Кожна з цих задач розв'язується в умовах ризику та невизначеності. Принцип оптимальності прийняття рішень для цих задач нерідко описується функцією корисності.

Корисність — ступінь задоволення суб'єкта від споживання това­ру (отримання послуги) чи виконання будь-якої дії.

В економічному аналізі корисність часто застосовують для того, щоб описати пріоритети у ранжуванні наборів споживчих товарів та послуг (за припущення, що людина завжди робить раціональний вибір, тобто обирає той варіант, корисність якого, на її думку, максимальна). Поняття функції корисності дає змогу порівняти споживчий ефект від купівлі (продажу) різних, навіть фізично несумісних, товарів. Корисність розглядають як узагальнені у певний спосіб витрати чи виграші, коли всі цінності зведено до однієї шкали. Для вимірювання корисності можна використовувати універсальну одиницю «ютил» (від англ. utility — корисність) або приводити показник до довільних одиниць (наприклад, грошових).

Для визначення корисності в умовах ризику вводять загальноприйняте поняття лотереї, де експерту пропону­ють порівняти дві альтернативи:

1) значення показника X;

2) лотерею — отримати Хmin з імовірністю (1-р) або Xmax з імовірністю р. Величину імовірності р змінюють доти, до­ки, на погляд експерта, значення показника X і лотерея L(Хmin, р, Xmax) не стануть еквівалентними (X L(Хmin, р, Xmax)). Корисність найгіршого результату зазвичай оціню­ється як 0 (U(Xmin) = 0), а найкращого — 1 або 100 (можуть бути довільні значення, але завжди U(Xmin) < U(Xmax)).

Приклад 1

Розглядають два варіанти інвестування коштів (20 тис. грн.):

1)придбання державних безризикових облігацій із доходом 1000 грн. (імовірність 1);

2) гра (лотерея): виграш 2100 грн. з імовірністю 0,5 і програш 50 грн. (накладні витрати на організацію) з імо­вірністю 0,5.

Необхідно дати рекомендації щодо напряму інвестування.

Розв’язання

1. Середній виграш:

— придбання державних облігацій 1000 × 1=1000 грн.;

• гра (лотерея) 2100×0,5-50×0,5 = 1025 грн.

Висновок: стосовно середнього виграшу розглянуті альтернативи майже еквівалентні, і якщо гравець нейтральний до ризику, він вибере другий варіант. Якщо він схильний чи несхильний До ризику, то вибір буде залежати від фінансового стану гравця. Гравці з незначним грошовим доходом не будуть ризикувати, віддадуть перевагу гарантованому виграшу. Для осіб із достатнім капіталом програш 50 грн. незначний, і вони ризикуватимуть. Обов'язково ризикуватимуть авантюристи (особи з патологічною схильністю до ризику).

Раціональну поведінку дослідили американські економісти Джон фон Нейман (1903—1957) та Оскар фон Моргенштерн (1902—1977)1. Вони вивели її основні аксіоми.

Аксіома 1 (повноти). Коли підприємець стикається з двома будь-якими низками подій, він завжди може визначити, чи якась із них йому більше до вподоби, або йому байдуже, яку послідовність подій вибрати: X > У (X більше до вподоби, ніж У); X ≥ У (X більше до вподоби або байдуже X чи У); X У (X і У рівноцінні). Ця аксіома є основою класифікації чи порівнювання послідовності подій, тобто дає змогу порівнювати всі альтернативи.

Аксіома 2 (транзитивності). Перевага різних низок подій послідовна, тобто, якщо X > У, У > Z, то X > Z. Це дає змогу уникнути фактора мінливості смаків суб'єкта (правильний вибір можливий лише за наявності усталеного смаку).

Аксіома 3 (неперервності). За умов дотримання аксіоми транзитивності, якщо суб'єкт з імовірністю 1 може отримати альтернативу X, імовірністю p і (1-р) — відповідно альтернативи У та Z, існує таке р, за якого набори X та У + Z рівноцінні.

Аксіома 4 (незалежності). Нехай існують блага X та У, які, за оцінкою суб'єкта, однакові, та дві лотереї, які відрізняються лише тим, що одна містить X, а друга — У, тоді ці дві лотереї для суб'єкта однакові.

Аксіома 5 (нерівних ймовірностей). Якщо суб'єктові запропонувати дві лотереї, які дають однаковий виграш із різною ймовірністю, то він обирає ту, ймовірність виграшу якої більша.

Аксіома 6 (складеної лотереї). Коли виграшем однієї лотереї є білет іншої лотереї, то суб'єкт приймає рішення лише з міркувань ймовірності кінцевого виграшу.

За Нейманом корисність варіанта X визначається імовірністю р(Х), при якій особі байдуже, що обирати: X — гарантовано, чи лотерею L(Хmin, р, Xmax).

Нехай лотерея L забезпечує виграш (події) Х1, Х2,..., Xn із відповідними ймовірностями p1, р2, …. рn і корисностями U(X1), U(Х2), ... U(Xn). Середній виграш (математичне сподівання) і очікувану (середню, найбільш імовірну) корисність визначають відповідно за формулами:

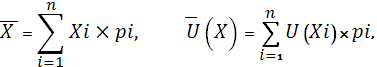
де X, U (Х) — середній виграш і очікувана (середня) корисність виграшу; Xi, — і-й варіант виграшу (події); рi — ймовірність і-го варіанта виграшу; U(Хi) — корисність і-го варіанта виграшу.

Взаємозв’язок ризику з функціями корисності визначається поняттям детермінованого еквіваленту. Детермінований еквівалент лотереї — це гарантована сума отримання якої еквівалентно участі в лотереї і гарантує особі таку саму корисність, як і участь у ризикованій справі, тобто

. (3.1)

Особу, що приймає рішення, називають несхильною до ризику, коли для неї найбільш пріоритетною є можливість одержати гарантовано очікуваний виграш у лотереї, ніж узяти в ній участь.

Із теорії корисності можна зробити висновок, що корисність лотереї збігається з математичним сподіванням корисності її випадкових результатів. Відповідно до цього умова несхильності до ризику набуває такого вигляду:

, (3.2)

тобто корисність сподіваного доходу більше сподіваної корисності. ОПР не схильна до ризику тоді й тільки тоді, коли її функція корисності увігнута.

Для функції корисності можна розрахувати премію за ризик у лотереї ((х)) як різницю між очікуваним виграшем і детермінованим еквівалентом:

. (3.3)

За своїм фізичним змістом премія за ризик (надбавка за ризик) — це сума в одиницях виміру показника X, якою суб’єкт управління згоден поступитися із середнього виграшу, щоб уникнути ризику, пов’язаного з лотереєю, і отримати гарантований дохід без ризику.

Коли особа, що приймає рішення, натрапляє на лотерею, менш пріоритетну, ніж стан, у якому вона в даний момент перебуває, то постає питання, скільки б вона заплатила (в одиницях вимірювання критерію X) за свою неучасть у цій лотереї (уникнення її).

Страхова сума (CC) — це величина детермінованого еквівалента з протилежним знаком:

. (3.4)

Умова схильності до ризику набуває такого вигляду:

, (3.5)

тобто корисність сподіваного доходу менше сподіваної корисності. ОПР схильна до ризику тоді й тільки тоді, коли її функція корисності опукла, а графік розгорнутий дзвоном униз. Премія за ризик у випадку схильності до ризику показує, скільки коштів інвестор може додатково отримати або втратити, ризикуючи.

Умова байдужості до ризику набуває такого вигляду:

. (3.6)

ОПР байдужа до ризику тоді й тільки тоді, коли її функція корисності лінійна, а графік — пряма. Премія за ризик у випадку байдужості до ризику завжди дорівнює нулю.

Розглянемо приклади функцій корисності:

Приклади різних функцій корисності:

1. U(Х) = а + bХ— зростаюча (при b > 0) або спадаюча (при b<0) функція корисності для суб'єкта, нейтрального до ризику (рис. 3.7);

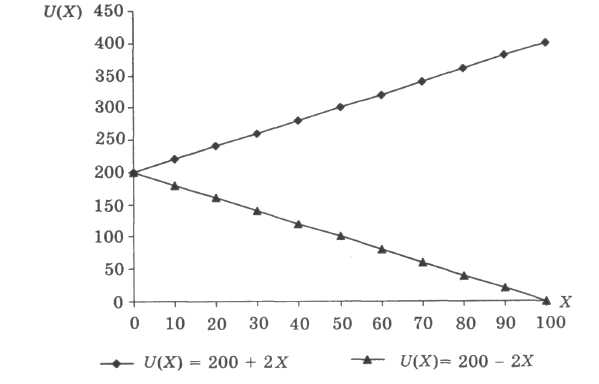
Рисунок 3.7. Зростаюча і спадаюча функція корисності для суб'єкта, нейтрального до ризику

2)U(Х) = 1оg_a(Х+b)— функція корисності для суб'єкта, несхильного до ризику, із зменшуваною корисністю (X > - b) (рис. 3.8);

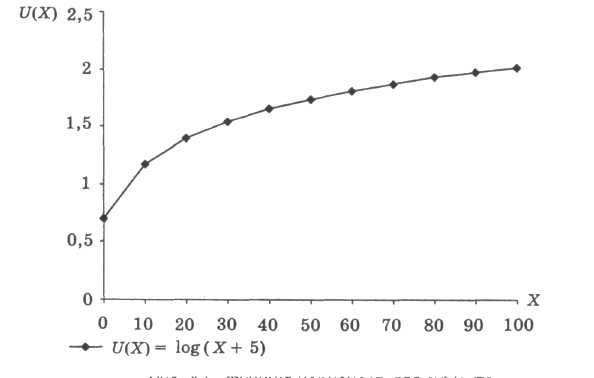
Рисунок 3.9. Функція корисності для суб'єкта, несхильного до ризику із зменшуваною корисністю

3) U(X) = e^cX — функція корисності для суб'єкта, постійно несхильного (при с>0) чи схильного (при с<0) до ризику (рис. 3.10);

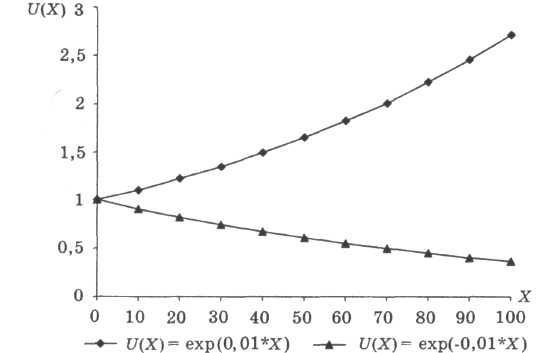
Рисунок 3.10. Функція корисності для суб'єкта, постійно несхильного чи схильного до ризику

4) U(Х) = сХ²— зростаюча функція корисності для суб'єкта, схильного (при c< 0) чи несхильного (при с < 0) до ризику (рис. 3.11);

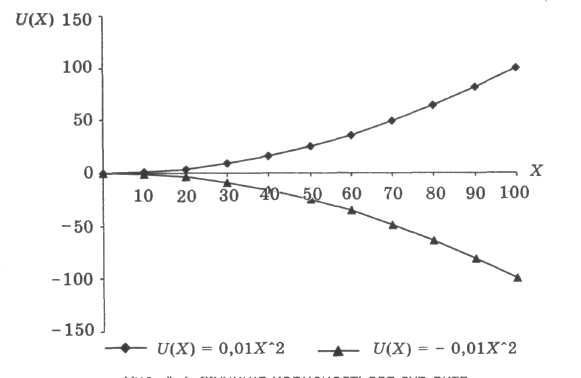
Рисунок 3.11. Функція корисності для суб'єкта із зростаючою схильністю чи несхильністю до ризику

5) U(Х) = а + bХ + СХ² (Х<b/с) — функція корисності для суб'єкта із зростаючою (при с < 0) або зменшуваною (при с>0) схильністю до ризику (рис. 3.12);

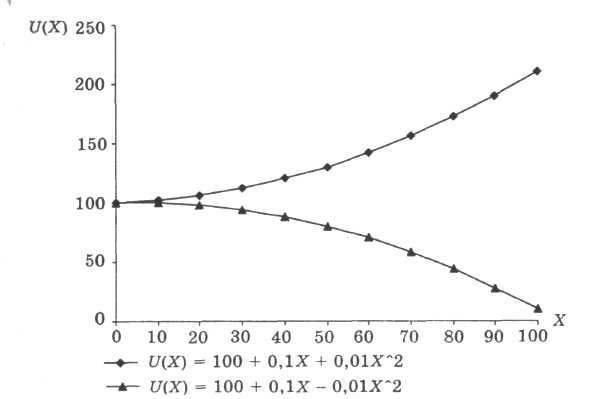
Рисунок 3.12. Функція корисності для суб'єкта із зростаючою або зменшуваною схильністю до ризику

6) U(X)= – функція з інтервальною нейтральністю (схильністю — несхильністю) до ризику (рис. 3.13).

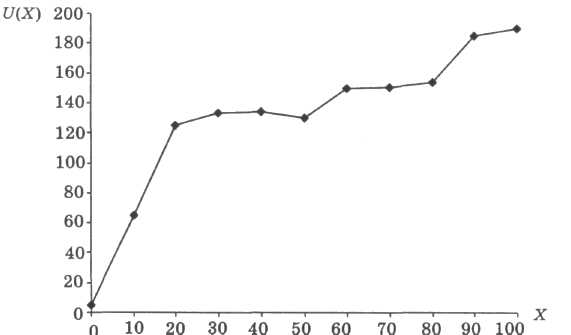
Рисунок 3.13. Функція корисності з інтервальною нейтральністю до ризику

На рис. 3.13 можна виокремити кілька зон схильності особи до ризику: (0;20) — нейтральність; (20;40) — несхильність; (40;60) — схильність; (60;80) — нейтральність; (80; 100) — несхильність; (0;50) — глобальна несхильність.

У теорії ринку цінних паперів широко використовується квадратична функція корисності вигляду:

, (3.7)

де А — задане число.

Зміст цієї функції такий: інвестор вважає корисним для себе збільшити значення ефективності, але бажає уникнути відхилення цієї ефективності від сподіваного значення. Чим більше А, тим більше тенденція запобігання ризику, тобто А — міра несхильнос­ті до ризику, а 1/А — міра схильності до ризику.

За допомогою функції корисності можна розраховувати ймовірність банкрутства:

, якщо ,

або 0, якщо ,

де K — початковий капітал.

Методика побудови функції корисності для будь-якого економічного показника складається з таких кроків:

Крок 1. Виявити найкращі та найгірші з можливих допустимих показників і присвоїти їм значення корисності відповідно 100 і 0 (якщо корисність оцінюється за 100-бальною шкалою).

Крок 2. Розглянути кілька проміжних показників і вказати їхнє значення корисності (кожним експертом окремо).

Крок 3. Розрахувати середні оцінки корисності проміжних значень, вказаних експертами.

Крок 4. Якщо спостерігається розсіювання значень якогось із показників, то потрібно повернутися до кроку 2, аби узгодити думки експертів для досягнення прийнятного діапазону розсіювання оцінок (кроки 2—4 можуть повторюватися кілька разів).

Крок 5. Визначення функції корисності через побудову функції регресії методом найменших квадратів (простіша функція корисності — рівняння прямої). Вид і аналітична форма функції корисності свідчить про відношення суб’єкта, що приймає рішення, до ризику.

Приклад 2

Визначення корисності за допомогою математичних функцій.

Фірма має прийняти рішення на основі трьох показників ефективності, застосовуючи різне відношення до ризику: несхильність, схильність, нейтральність. Показники ефективності задано лотереями: L1 = (20; 0,4; 10), L2 = (5; 0,5; 6), L3 = (10; 0,7; 30).

Несхильність до ризику задана функцією корисності: U(x) =

= 1 – 2e– 0,1x.

Схильність задано функцією корисності: U(x) = 0,4х.

Нейтральність задано функцією корисності: U(x) = 4 + 1,2х.

Розрахувати премію за ризик (надбавку) та визначити, яким відношенням до ризику має скористатися фірма.