2. Решение системы линейных уравнений

Теорема Кронекера – Капели

Пусть дана произвольная система m линейных уравнений с n неизвестными

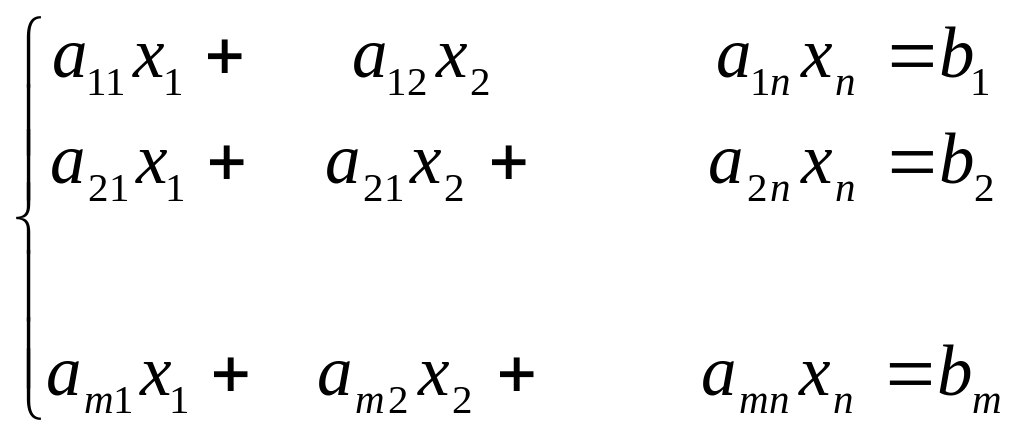
Исчерпывающий ответ на вопрос о совместимости этой системы дает теорема Кронекера – Капели (даю без доказательства)

Терема 1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Правила практического отыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.

Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Схема решения произвольной системы линейных уравнений:

1. Найти ранги основной и расширительной матриц системы, если r(A) ≠ r(Ā), то система не совместна.

2. Если r(A) = r(Ā) = r система совместна. Найти какой либо базисный минор порядка r (минор, порядок которого определяет ранг матрицы, называют базисным). Взять r уравнений из коэффициентов, которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называются главными, их оставляют слева, остальные n-r неизвестных называют свободными и переносят в правые части уравнений.

3. Найти выражение главных неизвестных через свободные. Получено общее решение системы.

4. Придавая свободным неизвестным произвольные значения получим соответствующие значения главных неизвестных. Таким образом, можно найти частные решения исходной системы уравнений.

Пример:

Решение: A= ,r(A)=1 A= ,r(A)=2

Таким образом, r(A) ≠ r(Ā), т.е. система не совместна.

3. Решение не вырожденных линейных систем.

Формулы Крамера

Пусть дана система п – линейных уравнений с п – неизвестными:

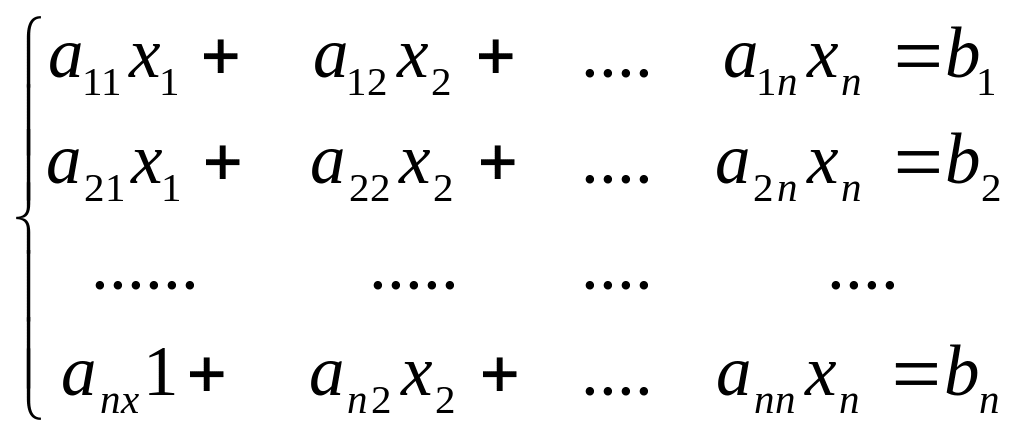
или в матричной форме АХ=В. Основная матрица А такой системы квадратная. Определитель этой матрицы:

∆=

называется определителем системы. Если ∆≠0, то система называется невырожденной.

Найдем решение данной системы уравнений в случае ∆≠0. Умножив, обе части уравнения =В на матрицу А^-1 получим . Поскольку =E и =Х, то Х=

Отыскание решения подобным образом называется матричным способом решения системы. Матричное решение запишем в виде:

= ∙

То есть

=

Отсюда следует, что ;

= ,

но А₁₁b₁+A₂₁b₂+…A_n1b_n есть разложение определителя

по элементам первого столбца. Определитель ∆₁ получается из определителя ∆ путем замены первого столбца коэффициентов, столбцом из свободных членов.

Аналогично , x₃= ……..x_n=

Формулы ; i=1,n - называют формулами Крамера.

Это второй способ решения невырожденной системы п – линейных уравнений с п – неизвестными.

Пример:

Решение: ∆= =7≠0, ∆ = =7, ∆ = =14

Значит х₁ = 1, х₂ = 2.