6) Признаки существования пределов.
Не всякая функция, даже ограниченная, имеет предел. Например: y=Sinx при x→∞ предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях удобно пользоваться признаками существования пределов.
Теорема 1. Если функция
f(x)
монотонна и ограничена при x<
x0 или
при x> x0,
то существует соответственно ее левый
предел
или ее правый предел
- без доказательства.
Следствие: если числовая последовательность
монотонна и ограниченна, то она имеет
предел.
Теорема 2.( О пределе
промежуточной функции) Если функция
f(x)
заключена между двумя функциями
(x)
и g(x),
стремящимися к одному и тому же пределу,
то они также стремится к этому пределу,
т.е. если
то
Доказательство: т.к.
и
то для любого
>0
найдется такое
>0,
что для всех x≠
x0 и
удовлетворяющих |x-x0|<
будут одновременно верны два неравенства
и
или
,
но т.к.
получается, что
,
т.е. | f(x)-A|<
,
а это означает, что
.
7) Первый замечательный предел.
Первым замечательным пределом называется:
Доказательство: возьмем круг радиуса 1. Обозначим радианную меру угла MOB через x (рис.3) Пусть 0<x<π/2;
M
C
y
1
B
x
A
O
или
Переходя к пределу при x→0
получим:
тогда по теореме о пределе промежуточной
функции получим:
Рис.3 при x>0
при x<0,
т.е.
при любых x.
Пример. Найти
8) Второй замечательный предел.
Как мы показали, предел числовой последовательности
Докажем, что к числу е стремится и
функция
при x→∞,т.е.
пусть x→+∞. Каждое значение x заключено между двумя целыми положительными числами
, где
-целая часть x. Отсюда
следует
поэтому
если
то и
поэтому
По теореме о пределе промежуточной функции получим:
Пусть
.
Сделаем подстановку –x=t,
тогда
Таким образом
,
если в этом уравнении положить
получим
Этот предел широко используется для вычисления других пределов.
Пример: Найти
.
Обозначив x=2t,
имеем
8) Сравнение бесконечно малых функций.
Отношение двух б.м.ф. может вести себя разным образом: быть конечным числом, бесконечно большой функцией , бесконечно малой или вообще не стремится ни к какому пределу.
Две б.м.ф. сравнивают с помощью их
отношения. Пусть
и
-есть б.м.ф. при x→x0,
т.е.
и
.
Тогда возможны четыре случая:
1. если
,
то α- бесконечно малая более высокого
порядка чем β;
2. если
,
то α и β- бесконечно малые одного порядка;
3. если
,
то α- бесконечно малая более низкого
порядка чем β;
4. если
- не существует, то α и β называют
несравнимыми бесконечно малыми.
9) Непрерывность функций.
Понятие непрерывности функции является фундаментальным в матанализе.
1. Функция f(x)
называется непрерывной в точке
x0,
если предел этой функции, и ее значение
в этой точке равны, т.е.
. (1)
Определение непрерывности можно дать и с позиций теоремы о пределах;
2. Функция f(x) называется непрерывной в точке х0, если для любого >0 существует такое >0, что при всех x удовлетворяющих неравенству |x-x0|< , выполняется неравенство |f(x)-f(x0)|< ;
3. Для практического использования
полезно сформулировать еще одно
определение непрерывности функции.
Назовем разность ∆x=x-x0-
приращением аргумента в точке x0
, а разность ∆y=f(x)-f(x0)-
приращением функции в точке x0,
обусловленное приращением аргумента
∆x. Таким образом,
∆x=x-x0,∆y=f(x)-f(x0),
поскольку условия x →x0
и x-x0
→0 равносильны, то равенство (1) можно
записать
-
еще одно определение непрерывности
функции.
10) Непрерывность функции в интервале и на отрезке.
Функция y=f(x)называется
непрерывной в интервале (a,b),
если она непрерывна в каждой точке этого
интервала. Функция y=f(x)
называется непрерывной на отрезке
[a,b],
если она непрерывна в интервале (
,b),
в точке x=
непрерывна справа(т.е.
),
а в точке x=b
непрерывна слева (т.е.
).
11) Точки разрыва и их классификация
Точка x0 называется точкой разрыва функции f(x) , если эта функция в данной точке не является непрерывной.
Различают точки разрыва:
Первого рода ( когда существуют односторонние конечные пределы функций слева и справа при x→ x0, не равные друг другу);
Второго рода (когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует)
Т
о
а)
+1
-1
б)
y=1/x
в)
ак
точка x1=0 на рис.
-
точка разрыва первого порядка, а на
рис.б)- точка разрыва второго порядка.
К точкам разрыва первого порядка
относятся также точки устранимого
разрыва, когда предел функции
при x→x0
существует, но не равен значению
функции в этой точке.
Н
Рис.4.
(рис.в). Точка x=0 этой
функции является точкой устранимого
разрыва. Положив y(x)=0
вместо y(x)=1,
при x=0, разрыв устранится.
Функция станет непрерывной.
12) Свойства функций.
а) для функций, непрерывных в точке:
Теорема о непрерывности функций вытекают непосредственно из соответствующих теорем о пределах.
Теорема 1. Сумма, произведение и частное двух непрерывных функций в точке x0 есть функция непрерывная( за исключением тех значений аргумента, в которых делитель равен нулю). Доказательство следует из теоремы о непрерывности и аналогичных свойств пределов функций.
Теорема 2. Пусть функция y=f(u) непрерывна в точке u0, а функция u= (x) непрерывна в точке u0=φ(x0). Тогда сложная функция y=f[φ(x)] непрерывна в точке x0.
Доказательство: в силу непрерывности
функции u=
(x),
,
т.е. при
x→ x0 имеем u→ u0. Поэтому вследствие непрерывности y=f(u) имеем:
Это доказывает, что функция y=f(φ(x)) непрерывна в x0.
Теорема 3. Если y=f(x) непрерывна в точке x0 и f(x0)>0, то существует такая окрестность точки x0, в которой f(x)>0.Доказательство основано на том, что малому приращению аргумента ∆x →0, соответствует какое угодно малое приращение ∆y в силу определения непрерывности. Так что знак функции y=f(x) в окрестностях (x0-∆x,x0+∆x) не изменится. Вообще следует отметить, что функция y=f(x) будет непрерывной на промежутке x, если она непрерывна в каждой точке этого промежутка. Можно доказать, что все элементарные функции непрерывны в области из значения.
б) для функций, непрерывных на отрезке:
Т
еорема1.
Если функция y=f(x)
непрерывна на отрезке [a,b],
то она ограничена на этом отрезке.
Теорема 2. Если функция y=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке своего наименьшего и наибольшего значения (теорема Вейерштрасса) (рис. a).
Теорема 3. Если функция y=f(x) непрерывна на отрезке [a,b] и принимает на его концах неравные значения f(a)=A и f(b)=B, то на этом отрезке она принимает все промежуточные значения между A и B.(рис.б)
Рис.5.
7. Производная.
Понятие производной относится к одному из основных понятий в математике. Она широко используется при решении задач, связанных с изменением различных функций во времени.
Пусть нам задана произвольная функция
на
некотором интервале
.
Придадим аргументу
приращение
.
Тогда соответствующее приращение
функции составит
.
Располагая этими значениями мы можем
ввести понятие производной функции в
точке
следующим
образом. Производной функции f(x)
в точке
называется
предел отношения приращения функции в
этой точке к приращению аргумента при
.
Итак, по определению производная
равна
или
Функция , имеющая производную в каждой точке интервала (a,b) называется дифференцируемой на этом интервале, а сама операция нахождения производной – дифференцированием.
Если функция имеет производную в каждой
точке множества Х, то и производная тоже
является функцией от аргумента
,
определенной на Х.
механический и геометрический смысл производной.
а) механический смысл.
Пусть
(t)
– вектор характеризующий положение
точки в различные моменты времени t.
Если мы зададим два момента времени t1
и t2, то вектор
изменится за промежуток
на
величину
,
и мы можем ввести понятие средней
скорости перемещения
.
Если мы возьмем предел от этого соотношения
при условии
,
то получим
,
где V будет определять
значение мгновенной скорости в момент
времени
.
Понятие производной можно использовать
при описании любого процесса зависящего
от времени и везде производная будет
определять скорость того или иного
процесса в какой-то конкретный момент
времени, в этом и состоит физический
смысл производной.
б) Геометрическая интерпретация.
П
Рис.6.
f(x1)
f(x0)
f(x2)
x2
x1
x0
М
усть
нам задана функция
изображенная на рисунке. По определению
производной:
,
но
,
тогда и
будет равен значению углового коэффициента
касательной проведенной к точке М
,в
этом и заключается геометрический смысл
производной.
2) связь между непрерывностью и дифференцируемостью функции.
Теорема. Если функции дифференцируема
в некоторой точке, то она и непрерывна
в ней. Обратное утверждение вообще
говоря не верно, т.е. если функция
непрерывна, то она необязательно
дифференцируема. Пример
в точке
эта функция непрерывна, но не
дифференцируема. Докажем теорему. Пусть
дана функция
дифференцируемая
в точке х0,
следовательно должен существовать
предел
, но в соответствии с теоремой о связи
функции, ее пределах и бесконечно малой
функции
,
где
при
отсюда
переходя к пределу при
получим
, что означает, что
– непрерывно в точке
.
Обратная теорема неверна: Примером
такой функции является
,
эта функция непрерывна в точке
,
но не дифференцируема в ней. Действительно
при
имеем:
Отсюда следует, что
не существует, т.е.
не имеет производной в точке
,
и график функции не имеет касательной
в точке О (0;0). В этом случае говорят, что
функция имеет односторонние производные
(справа и слева). Их обозначают, как
.
Не существует производных и в точках
разрыва функции.
Если функция
имеет непрерывную производную
в
некотором интервале
,
то функцию называют гладкой.
3) Производная суммы, разности и произведения и частного функции.
Нахождение производных функций, исходя из ее определения, иногда связано со значительными трудностями. Поэтому для упрощения процесса дифференцирования на практике используют ряд правил задаваемых с помощью нескольких теорем.
Пусть нам задано две дифференцируемые
на
функции
тогда:
Теорема 1 Производная суммы (разности)
двух функций равна сумме (разности)
производных, т.е.
Доказательство. Пусть
тогда,
или
.
В общем случае теорема справедлива для любого конечного числа слагаемых.
Теорема 2 Производная произведения
двух функций равно произведению
производной первого сомножителя на
второй плюс произведение первого
сомножителя на производную второго
т.е.
Пусть
,
тогда
Следствия: 1. можно показать, что
где С -
2.
Теорема 3 Производная частного двух
функций
,
если
равно дроби, числитель которой равен
разности произведения знаменателя
дроби на производную числителя и
числителя на производную знаменателя,
а знаменатель есть квадрат прежнего
знаменателя, т.е.
Доказательство. Пусть
, тогда
Следствия: 1)
2)
где С – const.
4)Производная сложной и обратной функции.
Пусть
и
,
тогда – сложная функция с промежуточным
аргументом и независимым аргументом
х. Для определения производной подобной
функции удобно пользоваться следующей
теоремой.
Теорема. Если функция имеет
производную
в точке х, а функция имеет производную
в соответствующей точке , то сложная
функция , имеет производную в точке х,
которая находится по формуле
;
Доказательство. Пусть
.
Отсюда, по теореме о связи функции, ее
пределе и б.м.ф. имеем
или
(1), где 
.
При 
,
функция имеет производную в точке х:,
поэтому
,
где
при
.
Подставив значение
в (1) получим
или
разделив на
и перейдя к пределу при
получим
Это правило остается в силе, если
промежуточных аргументов несколько.
Так если
а
то
,
если
,
а
,
то можно показать, что
.
5) Производная основных элементарных функций.
1. степенная функция
Схема доказательства
– раскладывается по формуле бинома
Ньютона и т.д. и получаем все что надо.
2. Показательная функция
.
Докажем сначала для
берем предел при
.(Использовали
=∆x,
при x→0)
Т.е.
Теперь пусть
и дифференцируя
как сложную функцию получим
3. Логарифмическая функция
Найдем сначала производную от
Поскольку
при
полчучим:
т.е.
но т.к.
то
4. Тригонометрические функции.
Для
имеем
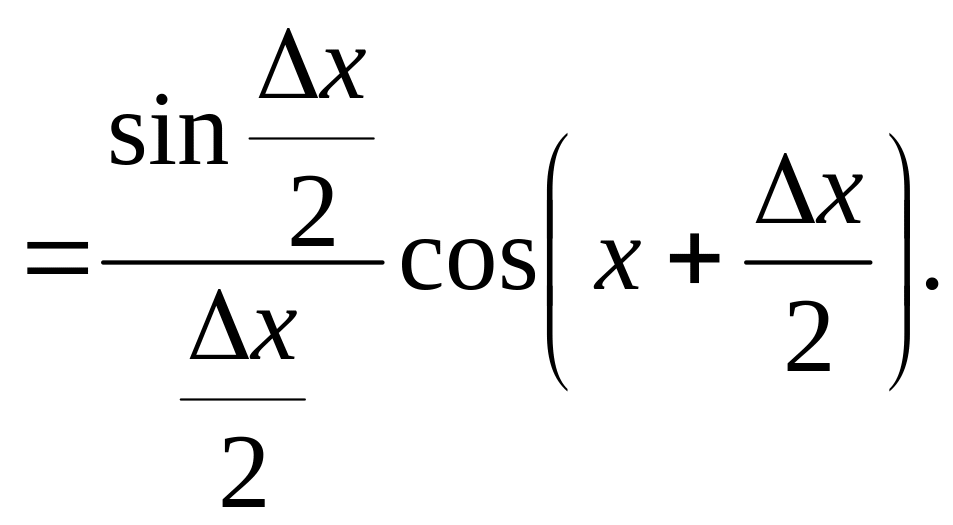
Т.е.
или
Проделав аналогичные преобразования можно получить:
а)
б)
в)
5. Точно таким же образом находятся формулы для расчета производных обратных тригонометрических функций.
а)
б)
в)
г)
Обобщив все полученные выше правила и выведенные соотношения можно получить так называемую таблицу производных:
6) Таблица дифференцирования:
1.
2.
3.
;
4.
если
а
5.
если
а
Формулы дифференцирования:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
7) Дифференцирование неявных и параметрических заданных функций.
1) Если функция задана уравнением y=f(x), решенным относительно y, то функция задана в явном виде(явная функция). Под неявным заданием функции понимают задание функции в виде уравнения F(x,y)=0 не разрешенного относительно y. Всякую явно заданную функцию можно записать как неявно заданную уравнением F(x)-y=0, но не наоборот.
Не всегда легко, а иногда и невозможно
разрешить уравнение относительно y
(например: y+2x+cosy-1=0).
Если неявная функция задана уравнением
F(x,y)=0,
то для нахождения производной y
по x нет необходимости
разрешать уравнение относительно y.
Достаточно продифференцировать это
уравнение по x,
рассматривая при этом y
как функцию x,
и полученное затем уравнение разрешить
относительно
.
Производная неявной функции выражается
через аргумент x и функцию
y.
Пример: найти производную функции
y заданную уравнением :
Дифференцируя по, x
получим:
,
т.е.
;
2. Функция заданная параметрически. Пусть зависимость между аргументом x и функцией y задана параметрически в виде уравнений
где t- вспомогательная переменная, называемая параметром.
Найдем y'x , считая, что записанные функции имеют производные и что функция x=x(t) имеет обратную функцию t=φ(x). По правилу дифференцирования обратной функции
Функцию y=f(x) можно рассматривать как сложную функцию y=y(t), где t=φ(x), тогда по правилу дифференцирования сложной функции
Или
т.е.
Полученное соотношение позволяет находить производную y'x от функции заданной параметрически, не находя непосредственную зависимость y от x.
Пример :
найти
.Тогда
В правильности полученного соотношения
легко убедиться. Действительно
тогда
отсюда
т.е.
8) Логарифмическое дифференцирование
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем результат продифференцировать.
Такую операцию и называют логарифмическим дифференцированием.
Пример: найти производную функции:
Прологарифмируя это соотношение, получим:
Дифференцируя по x получим
:
Найдем
=y
или
=
;
Существуют функции производные, которых
можно найти лишь логарифмическим
дифференцированием. К их числу относятся
так называемые степенно-показательные
функции: y=
, где u=u(x)
и
=
(x).
Найдем производную этой функции
.
Логарифмируем:
Дифференцируем:
Или
Или
.
9) Производные высших порядков
Производные высших порядков явно заданной функции.
Производная y'x=f
'(x) функции y=f(x),
есть также функция от x
и называется производной первого
порядка. Если функция
(x)
дифференцируема, то ее производная
называется производной второго
порядка и обозначается :
Итак, y''=(y')'.
Производной от y'', если она существует, называется производной третьего порядка y'''=(y'')' и т.д.
Производной n-го порядка называется производная от производной (n-1) порядка
Производные порядка выше первого называются производными высших порядков.
Смысл производной второго порядка ( механический)
Рассмотрим ту же задачу, которую мы рассматривали для определения механического смысла первой производной.
Точка M движется по произвольной линии тогда:
(мгновенная
скорость точки в данный момент времени).
Пусть в момент времени t, скорость равна V, а в момент t+∆t скорость равно V+∆V,тогда
- эта величина показывает изменение скорости за сколько угодно малый промежуток времени и в механике она называется ускорением в данный момент времени.
Производные высших порядков неявно заданной функции.
Пустьy=f(x) задана неявно F(x,y)=0. Продифференцировав это уравнение по x, и разрешив относительно y' найдем первую производную. Продифференцировав еще раз найдем вторую и т.д.
Производные высших порядков от функции заданной параметрически
Пусть y=f(x) задана параметрически:
Как известно y'x
=
. Найдем y''x
.
Т.к.
как обратные функции ,то
10) Дифференциал функции
Пусть функция y=f(x) имеет в точке x отличную от нуля производную f '(x)≠0, тогда по теореме о связи функции, ее пределом и бесконечно малой функции можно записать
,где
α→0 при ∆x→0 или
Таким образом, приращение функции ∆y представляет собой сумму двух слагаемых f '(x)∆x и α∆x являющихся бесконечно малыми при ∆x→0. при этом первое слагаемое есть бесконечно малая функция одного порядка с ∆x, так как
,
а второе слагаемое есть бесконечно
малая функция более высокого порядка,
чем ∆x:
Поэтому первое слагаемое f '(x)∆x называют главной частью приращения функции ∆y.
Дифференциалом функции y=f(x) в точке x и называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy(или d(f(x)). По определению: dy= (x)dx
Иными словами.
Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Пример: найти дифференциал
11) .Геометрический смысл дифференциала функции
П
роведем
к графику y=f(x)
в точке M(x,y)
касательную MT и рассмотрим
ординату этой касательной для точки
x+∆x (рис.7).
На рисунке |AM|=∆x,
|AM1|=∆y
из ∆MAB имеем
dy
Рис.7.
(x)∆x.
Сравнивая полученный результат с определением дифференциала, получаем dy=AB, т.е. дифференциал функции в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение ∆x.
12) Основные теоремы о дифференциалах
Они вытекают из теоремы о производных. Например, т.к. y'=0 при y=c, то дифференциал постоянной величины c тоже равен нулю dy=c'dx=0.
Теорема 1. дифференциал суммы, произведения и частного двух дифференцируемых функций определяется следующими формулами
при V≠0
Докажем, например, правильность второй формулы. По определению дифференциала имеем:
d(UV)=(UV)'dx=(U'V+UV')dx=VU'dx+UV'dx=Vdu+Udv
Теорема 2. дифференциал сложной функции равен произведению этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пусть y=f(u) и u=φ(x)- две дифференцируемые функции образующие сложную функцию: y=f(φ(x)). По теореме о производной сложной функции можно написать y'x=y'uu'x. Умножив обе части этого равенства на dx, получим: y'xdx=dy=y'uu'xdx, учитывая, что u'xdx=du, получим: dy=y'udu. Итак, дифференциал определяется одной и той же формулой, не зависимо от того, является ли ее аргумент независимой переменной или нет.
Это свойство дифференциала называют
инвариантностью (неизменностью) формы
первого дифференциала. При этом
необходимо учитывать, что если dx=
x,
то u есть функция от x,
поэтому, вообще говоря, du≠∆u.
С помощью определения дифференциала можно легко преобразовать таблицу производных в таблицу дифференциалов:
1)
2)d(UV)=VdU+Ud , в частности d(CU)=CdU
3)
,
в частности d
и т.д.
13) Применение дифференциала к приближенным вычислениям.
Как говорилось выше, приращение функции
∆y в точке x
можно представить в виде
∆y=
(x)∆x+α∆x,
где α→0 при x→0, или
∆y=dy+α∆x.
Отбрасывая бесконечно малую величину
α∆x более высокого порядка,
чем ∆x, получим приближенное
равенство: ∆y≈ dy.
Причем это равенство тем точнее, чем
меньше ∆x.
Это равенство позволяет с большой точностью вычислять приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, поэтому это соотношение широко применяется на практике.
Пример: найти приближенное значение
функции
, при x=2 и ∆x=0,001.
Решение:
dy=
.
Итак,
Определим, какую погрешность мы допустили при этом приближенном вычислении. Для этого найдем точное значение ∆y
Абсолютная погрешность составит
Формулу приближенных соотношений обычно записывают в виде:
14) Дифференциалы высших порядков
Пусть функция y=f(x)- дифференцируемая функция, а ее аргумент x- независимая переменная. Тогда ее первый дифференциал dy=f '(x)dx есть также функция x и можно найти дифференциал этой функции .
Дифференциал от дифференциала функции y=f(x) называется дифференциалом второго порядка (вторым дифференциалом) обозначается d2y=d(dy).
Итак, по определению d2y=d(dy). Найдем выражение для d2y. Так как dx=∆x не зависит от x, то при дифференцировании считаем dx- const:
Т.е.
Аналогично можно записать, что дифференциал n-го порядка определяется согласно соотношению:
Т.е. дифференциал второго порядка и (вообще n-го) порядка равен произведению производной второго порядка (n-го) на квадрат (n-ю степень) дифференциала независимой переменной.
Из этих соотношений следует, что
В заключении отметим, что эти соотношения справедливы только в случае если
x-независимая переменная. Если же y=f(x), где x- функция другого аргумента, то дифференциалы высших порядков (n>1) не обладают свойством инвариантности и вычисляются по другим формулам.
6. Исследование функций с помощью методов дифференциального исчисления.
1) Основные теоремы о дифференцируемых функциях.
Теорема 1. (Ролля) Если f(x)
непрерывна на [
,b]
и дифференцируема на интервале (
,b)
и на концах отрезка принимает одинаковые
значения f(
)=f(b),
то найдется хотя бы одна точка С
в которой f '(x)=0,
т.е. f '(c)=0.
Так как функция f(х)
непрерывна на [
,b],
то она достигает на этом отрезке своего
наибольшего и наименьшего значения
соответственно М и m. Если
М
m, f(x)=
const на [
,b]
и следовательно
=0
в любой точке [
,b].
Если М ≠ m, то функция
достигает хотя бы одно из значений М
или m во внутренней точки
С интервала [
,b],
так как f(
)=f(b).
Пусть например, функция принимает
значение М в точке
(
,b),
т.е. f(с)=М, тогда для всех
выполняется соотношение
Найдем
в точке х=с.
В силу неравенства f(x)<
f (с),
,
если
т.е.
справа от точки
то
и
Если
Таким образом f '(с) =0. В
случае, когда
=
m доказательство носит
аналогичный характер.
Геометрически теорема Ролля означает, что на графике функции y=f'(х) найдется точка в которой касательная параллельна к графику параллельна оси ох. (рис.8.)
М
М
б)
m
в)
a
b
m
b
b
Рис.8.
Теорема 2 (Коши) Если функции f(x)
и
(x) непрерывны на [
,b],
дифференцируемы на интервале (
,b),
причем
для
,
то найдется хотя бы одна точка
такая, что выполняется равенство
Для доказательства теоремы рассмотрим
вспомогательную функцию
она удовлетворяет всем условиям теоремы
Ролля: непрерывна на [
,b]
и дифференцируема на (
,b),
так как является линейной комбинацией
функций f(x)
и
;
на концах отрезка она принимает
одинаковые значения F(
)=F(b)=0.
Поэтому на основании теоремы Ролля
найдется
такая, что
,
но
следовательно
отсюда следует
и
Что и требовалось доказать.
Теорема 3. (Лагранжа). Если функция f(x) непрерывна на [ ,b], дифференцируема на интервале ( ,b), то найдется хотя бы одна точка такая, что выполняется равенство f(b)-f( )=f '(c)(b- ).
Полученную формулу называют формулой Лагранжа или формулой о конечном приращении.
Теорему Лагранжа можно рассматривать
как частный случай теоремы Коши. Положив
,
найдем
.
Подставив эти три значения в формулу
Коши
получим
или
.
Т
С
В
А
еорема
Лагранжа имеет простой геометрический
смысл.
левая часть этого соотношения есть
угловой коэффициент прямой линии
соединяющей точки А и В, а величина f
'(c) – угловой коэффициент
касательной в точке с абсциссой х=с.
С
с
б
a
Рис.9.
Правило Лопиталя.
Рассмотрим способ раскрытия
неопределенностей вида
и
,
который основан на методах дифференциального
исчисления.
а) Теорема 1. (Правило Лопиталя раскрытия
неопределенностей вида
).
Пусть функции f(x)
и
непрерывны и дифференцируемы в
окрестностях точки
и обращаются в ноль в этой точке:
.
Пусть
в окрестностях
,
тогда если существует предел
то
Доказательство. Применим к функциям
f(x) и
теорему Коши для отрезка [
,
]
лежащего в окрестностях
.
Тогда
где с лежит между
и
.
Учитывая, что
,
получим
при
величина с также стремится к
и если перейдем к пределу ,то получим
,
так как
,то
и
Поэтому
что и требовалось доказать.
Эта теорема справедлива и в случае, если
.
Действительно проложив
,
получим:
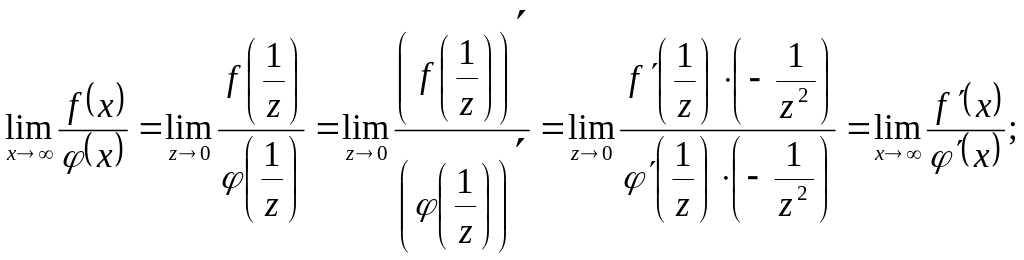
б) Теорема 2. (Правило Лопиталя раскрытия неопределенностей вида ).
Пусть функции
и
непрерывны и дифференцируемы в
окрестностях точки
(кроме может быть самой точки
)
кроме того, в этой окрестности
,
а
и если существует
то
Без доказательства.
Примеры:
Найти
в) Раскрытие неопределенностей различных видов.
Правило Лопиталя применяется для
раскрытия неопределенностей
и
,
которые называется основными. Но его
можно применять и для раскрытия других
неопределенностей типа
которые сводятся к основным путем
тождественных преобразований.
Пусть
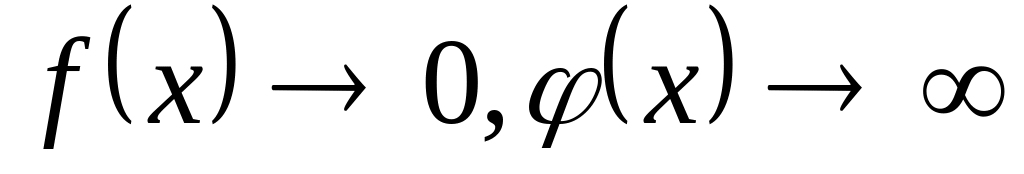при
тогда
Пусть
при
тогда
И так далее.
Пример:
Возрастание и убывание функций.
Одним из приложений дифференциального исчисления является его применение к исследованию функций и построению графика функций.
Теорема 1. (необходимые условия) Если
дифференцируемая на интервале (
,b)
функция f(x)
возрастает (убывает), то
Пусть функция f(x)
возрастает на интервале (
,b).
Возьмем произвольные точки х и
на интервале (
,b)
и рассмотрим отношение
.
Функция f(x)
возрастает, поэтому, если
,
то
и
,
если
,
то
и
.
В обоих случаях
,
так как числитель и знаменатель имеют
одинаковые знаки. По условию теоремы
функция f(x)
имеет производную в точке х которая и
является пределом рассматриваемого
отношения, следовательно
Аналогичным образом рассматривается и случай, когда f(x) убывает на интервале ( ,b). Геометрически эта теорема обозначает, что касательные к графику возрастающей функции образуют острые углы с положительным направлением оси Ох.
Теорема 2. (достаточные условия).
Если
дифференцируема на интервале (
,b)
и f '(х)>0 (f
'(х)<0) для
,
то эта функция возрастает (убывает) на
(
,b).
Пусть f '(х) >0. Возьмем
точки х1 и х2 на (
,b),
причем х1<х2. Применим к
отрезку [х1,х2] теорему
Лагранжа: f(x2)
– f(x1)=
f '(c)(x2-x1),
где
.
По условию f '(c)>0,
х2-х1>0. следовательно f(x2)
– f(x1)>0
или f(x2)
> f(x1)
т.е. f(x) на
интервале (
,b)
возрастает.
Максимум и минимум функции.
Точка
называется точкой максимума y=f(x),
если существует такая δ-окрестность
точки
,
что для всех
из этой окрестности выполняется
неравенство f(x)<f(x0).
Аналогичным образом определяется точка
минимума функции.
– точка минимума функции, если для
всех
из δ – окрестности выполняется
неравенство f(x)>f(
).
(рис.10)
З
f(x)
начения
функции в точках максимума и минимума
называются максимумом (минимумом)
функции или экстремумом. Понятие
экстремума всегда связано с определенной
окрестностью точки из области определения
функции. Поэтому функция может иметь
экстремум только во внутренних точках
области определения.
Р
Рис.10
Теорема 1. (необходимое существование экстремума)
Если дифференцируемая функция y = f(x) имеет экстремум в точке , то её производная в этой точке равна нулю f '(х) = 0.
Доказательство.
Пусть – точка максимума. Значит в окрестностях x0 выполняется неравенство
f(
)
> f(
+
x),
но тогда
=
< 0, если
и
>
0, если
0.
По условию теоремы
существует и в соответствии с вышесказанным
,
если
и
,
если
.
Поэтому
.
Аналогичным образом доказывают теорему если - точка минимума функции.
Геометрически равенство
означает, что в точке экстремума функции
,
касательная к ее графику параллельна
оси OX. Надо отметить, что
обратная теорема не верна т.е. если
,
то это не означает, что в
- точка экстремума.
(Например
при x=0, но это не точка
экстремума ).
Теорема 2 (достаточное условие экстремума)
Если непрерывная функция
дифференцируемая в некоторой
-окрестности точки
и при переходе через нее (слева на право)
производная
меняет знак с плюса на минус, то
- точка максимума, с минуса на плюс, то
точка
- точка минимума.
Рассмотрим
-
окрестности точки
.
Пусть выполняются условия
,
и
,
.
Тогда функция
возрастает на интервале
,
а на интервале
она убывает. Отсюда следует, что значение
в точке
является наибольшем на интервале
т.е
для всех
.
Это и означает, что точка
- точка максимума функции. Аналогичным
образом эта теорема доказывается и для
случая когда
.Графическая
интерпретация этого доказательства
представлена на Рис.11.
И
сследовать
функцию на экстремум означает найти
все её экстремумы по следующим правилам:
Н
айти критические точки функции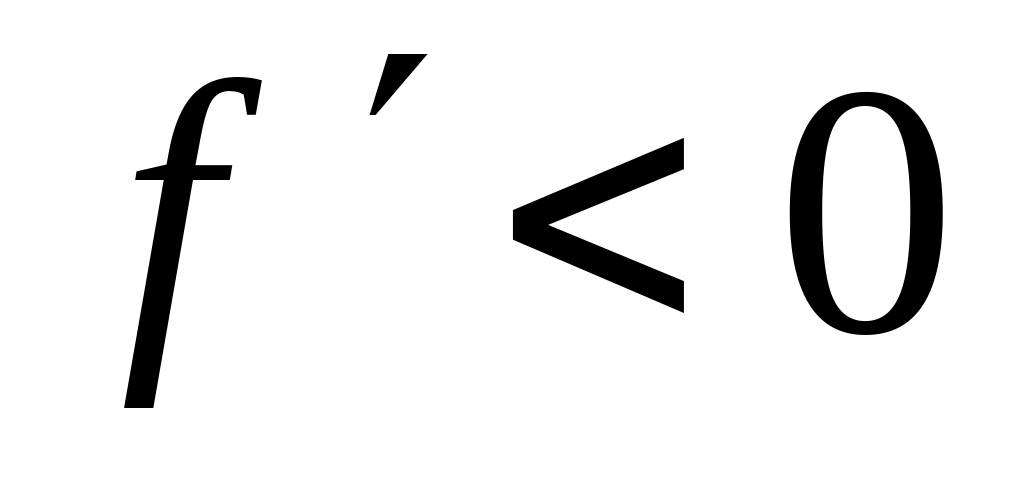
.Выбрать из них те которые являются внутренними точками области определения функции.
Исследовать знак слева и справа от каждой из
Рис.11 выбранных критических точек.
В соответствии с теоремой в достаточном условии экстремума определить точки экстремумов и вычислить значение функции в них.
Иногда для определения достаточных условий экстремума бывает удобным использовать другой способ основанный на определении знака второй производной!
Теорема 3 Если в точке
первая
производная функции
равна нулю
,
а вторая производная в точке
существует и отлична от нуля
,
то при
в точке
функция имеет максимум, а при
-
минимум.
Пусть
.
Так как
,
то
,
если
,
то
;
если
,
то
.
Таким образом при переходе через точку
первая производная меняет знак с минуса
на плюс. Следовательно по теореме 2,
-
есть точка минимума. Аналогично
доказывается, что если
,
то в точке
функция имеет максимум.
5) Выпуклости функции. Точки перегиба.
График функции называется выпуклым вниз на интервале , если он расположен выше любой ее касательной на этом интервале. Точка графика непрерывной функции , отделяющая его части разной выпуклости, называется точкой перегиба.
Н
y
М
у=f(x)
а
рис.12 кривая
выпукла вверх на интервале
,
выпукла вниз на
,
а точка М
- точка перегиба.
И
нтервалы
выпуклости вниз и вверх находятся с
помощью следующей теоремы.
Т
Рис.12.
x
с
во всех точках интервала
имеет отрицательную вторую производную
т.е
,
то график функции в этом интервале
выпуклый вверх. Если же
- график функции выпуклый вниз.
Доказательство:
П
усть
при
.
Возьмем на графике функции произвольную
точку М с абсциссой
и проведем через точку М касательную
(рис.13).
Рис.13.
Покажем, что график функции расположен ниже этой касательной.
Для этого сравним в точке
,
ординату кривой
с ординатой
(ее касательной). Уравнение касательной
как известно записывается следующим
образом.
,
т.е.
.
Тогда
.
По теореме Лагранжа
,
где
лежит между
и
.
Поэтому
.
Разность
преобразуем по формуле Лагранжа
,где
лежит между
и
.
Тогда получим
.
Рассмотрим варианты:
Пусть
1) Если
,
то
,
и
.
Следовательно
т.е.
.
2) Если
,
то
,
и
.
Следовательно
т.е.
.
Итак мы доказали, что во всех точках интервала ордината касательной больше ординаты графика, т.е. график функции выпуклый вверх.
Аналогично доказывается, что при
график выпуклый вниз. Для нахождения
точек перегиба используется теорема
2.
Теорема 2 (достаточное условие существование точек перегиба)
Если вторая производная
при переходе через точку
,
в которой она равна нулю или не
существует, меняет знак, то, эта точка
- есть точка перегиба.
Доказательство:
Пусть
при
и
при
.
Это значит, что слева от
график
выпуклый вверх, а справа выпуклый вниз.
Следовательно, точка
графика функции является точкой перегиба.
Аналогично доказывается, что если
при
и
при
,
то точка
- точка перегиба функции
.
Пример:
- исследовать на выпуклость и точки
перегиба.
,
.
Вторая производная существует на всей
действительной оси.
при
:
при
и
при
.
Следовательно график функции
в интервале
выпуклый вверх, в интервале
- выпуклый вниз. Точка
есть точка перегиба.
Асимптоты графика функции.
Построение графика функции значительно упрощается если предварительно построены ее асимптоты. Ранее говорилось, что асимптота – прямая расстояние которой от функции стремится к нулю при неограниченном увеличении аргумента.
Различают асимптоты вертикальные,
горизонтальные и наклонные, в зависимости
от угла образованного ими с осью абсцисс.
Вертикальная асимптота определяется
уравнением
,
горизонтальная
,
а наклонная в виде уравнения прямой
.
Найдем, в случаи произвольной функции
,
значения
и
для наклонной асимптоты.
M(x,y)
d
y=kx+b
у=f(x)
Рис.14.
- произвольная точка кривой
(Рис.14). По формуле расстояния от точки
до прямой
.
Найдем расстояние от точки M
до прямой
.
Условие
будет реализовано тогда, когда числитель
дроби стремится к нулю т.е.
.
(1)
Отсюда
,
где
- б.м.ф.
при
.
Разделив уравнение (1) на
и перейдя к пределу при
получим:
т.к.
и
,
то
,
а
.
Эти соотношения и позволяют определить
параметры наклонных асимптот. Если один
из пределов не существует или равен
бесконечности, то для функции
наклонных асимптот не существует.
Следует отметить, что иногда асимптоты
функции
при
и
могут быть разными. Поэтому их надо
находить по отдельности.
Общая схема исследования функции .
Найти область определения функции
Найти точки пересечения функции с осями координат.
Найти интервал знакопостоянства и определить будет функция четной или нечетной.
Найти асимптоты
Найти интервал монотонности и точки разрыва.
Найти точки экстремумов функции.
Найти интервалы выпуклости и точки перегиба.
На основании полученных результатов построить график.
Пример:
.
1. Область определения
,
- три ветви графика .
2. Если х=0, то y=0 и график проходит через т. О(0,0).
3. Функция является нечетной, т.е. график
симметричен относительно т. О
и
при
и
,
и
при
и
.
4. Прямые
и
-
вертикальные асимптоты.
Определим наличие наклонных асимптот
(
при
и при
).
.
Следовательно существует, помимо
вертикальных, еще и горизонтальная
асимптота
.
(при
и при
).
5. Найдем интервалы возрастания и убывания функции.
Так
и
т.е. функция будет возрастающей в каждом
интервале определения.
6. Найдем max и min.
Т.к.
,
то критические точки
и
,
но они к области определения не
принадлежат. Следовательно функция
экстремумов не имеет.
7. Найдем области выпуклости.
Вторая производная равна нулю или не
существует в точках
,
Точка О
- точка перегиба функции. График выпуклый
вверх на интервалах
и
,
выпуклый вниз на интервалах
и
.
График функции будет иметь следующий
вид (Рис.15)
Рис. 15
7
В определении функции y=f(x) не говорится как найти значения y по значениям x. В случае простых соотношений это можно сделать с помощью арифметических действий, но как быть, если функциональная зависимость задана более сложным образом? Например, y= Sinx, y=ln(x+1) и т.д. Существует приближенный способ, при котором функцию заменяют многочленом Pn(x) степени n, значения которого всегда можно вычислить. Обоснование возможности представить функцию многочленом дает формула Тейлора.
1) Формула Тейлора для многочлена
Пусть f(x) есть многочлен Pn(x) степени n:т.е.
Преобразуем этот многочлен в многочлен степени n относительно разности x-x0 , где x0 – произвольное число, т.е. представим Pn(x) в виде:
(1)
для нахождения коэффициентов A0,A1....An продифференцируем это соотношение n раз:
…………………….
Подставляя x=x0 и используя (1) получим:
т.е.
…………………………
Подставляя полученное соотношение в (1) получим разложение многочлена n-й степени Pn(x) по степеням (x-x0):
Это и есть формула Тейлора для многочлена Pn(x) степени n.
2) Формула Тейлора для произвольной функции.
рассмотрим функцию y=f(x). Формула Тейлора позволяет, при определенных условиях, приближенно представить функцию f(x) в виде многочлена и дать оценку погрешности этого приближения.
Теорема 1.(Теорема
Тейлора).Если функция f(x)=y
определена в некоторой окрестности
точки x0
и имеет в ней производные до (n+1)-го
порядка включительно, то для любого x
из этой окрестности найдется такая
точка c
(x0,x),
что справедлива следующая формула:
Эта формула называется формулой Тейлора для функции f(x). Эту формулу можно записать в виде:
-называется
многочленом Тейлора, а
-называется остаточным членом
формулы Тейлора, записанном в
форме Лагранжа .
Rn(x) - есть погрешность приближенного равенства f(x) ≈ Pn(x). Таким образом, формула Тейлора дает возможность заменить функцию y=f(x) многочленом Pn(x) с соответствующей степенью точности, равной значению остаточного члена Rn(x).
При x0=0 получаем частный случай формулы Тейлора – формулу Макларена:
, где c находится
между 0 и x(c=
x,0<
<1).
При n=0 , формула Тейлора
имеет вид
или
,
т.е. совпадает с формулой Лагранжа
конечных приращений. Рассмотренная
ранее формула для приближенных вычислений:
является частным случаем более точной
формулы:
Примеры:
1. Разложение в ряд функции ex.
Запишем формулу Макларена для f(x)=ex.
Для этого найдем производные этой
функции:
.
Так как
то по формуле Макларена имеем:
Это соотношение используется для вычисления числа е с любой необходимой точностью. Запишем ее с остаточным членом в форме Лагранжа при x=1
Для нахождения е с точностью 0,001
определим n из
условий, что остаточный член
меньше 0,001. Так как 0<c<1,
то еc<3,
поэтому при n=6
имеем:
Итак,
получаем приближенное равенство:
, т.е. е ≈2,718
2. у=sinx,
и
т.д.
При x=0;
и
т.д.
Очевидно, что производные четного
порядка
, а нечетного порядка
и подставляя в формулу Макларена
получим:
3. y=cosx. Производя аналогичные операции, получим:
4. y=(1+x)m , где m- любое действительное число. Имеем:
….
.При
x=0,
)
И по формуле Макларена получим:
5. y=ln(1+x).
Так как
,то
подставляя, получим:
При разрешении более сложных функций используют либо непосредственно формулу Макларена либо вышеприведенные соотношения для простейших разложений.
Пример: разложить в ряд функцию
.
Так как
то
заменяя x на (-x2),
получим:
и наконец:
3. Приближенные вычисления
Разложение функций в многочлены по формулам Тейлора( Макларена) позволяет(как это было показано для случая вычисления числа е) получать приближенное значение функций при заданных значениях аргумента. Рассмотрим несколько примеров связанных с таким расчетом:
Пример 1: вычислим приближенно с точностью до 0,0001 y=lnx, если x=0,8.
Воспользуемся для вычисления выражением
.
При x=-0,2.
Если взять первые четыре члена, то при расчете ln0,8 мы допустим погрешность
Мы учли, что сумма сходящихся геометрического ряда в скобках равна
Итак, получаем, что
Пример 2: вычислим приближенно с
точностью до 0,0001 величину равную
.
Представим
в виде
, полагая x=⅛ и
m=1/5 можно записать:
.
Т.е. можем воспользоваться полученным
ранее соотношением:
Подставляя значения, получим:
=2+0,05-0,0025+0,000188-0,0000016+…≈2,0477.
Для обеспечения заданной точности
расчета необходимо взять четыре члена,
так как остаточный член по Лейбницу в
этом случае
