3. Невырожденные матрицы

Пусть А – квадратная матрица n-го порядка.

A=

Эта матрица называется невырожденной, если ∆≠0, в противном случае ∆=0 и матрица – вырожденная.

Обратная матрица

Матрица А^-1 называется обратной матрице А, если выполняется условие – единичная матрица того же порядка, что и матрица А. Матрица А^-1 имеет те же размеры, что и матрица А.

Теорема: Всякая невырожденная матрица имеет обратную.

Проведем доказательство для случая матрицы 3-го порядка. Пусть

A= , причем ∆≠0

Рассмотрим квадратную матрицу А^* ,называемую союзной, элементы которой являются алгебраическими дополнениями элемента _ij данной матрицы А (определяется так же, как и алгебраическое дополнение элемента определителя).

A^* =

И найдем произведение А на А^*

A∙A*= =

=

Используя свойства 6) и 7 получим)

= = = (1)

Аналогично можно показать, что (2).Равенство (1) и (2) можно записать в виде:

и

Сравнивая эти выражения с определением обратной матрицы, получим: A^-1 =

Свойства обратных матриц:

1)

2)

3)

2. Ранг матрицы

Рассмотрим матрицу А размера m×n.

A =

В этой матрице вычеркиванием, каких либо строк и столбцов можно вычленить квадратные подматрицы k-го порядка, где k ≤ min (m,n). Все такие определители, как мы говорили ранее, называются минорами. Наибольший порядок миноров, отличных от нуля называется рангом матрицы. Обозначается r, r(A) или rang A, очевидно, что 0 ≤ r ≤ min (m,n).

Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором этой матрицы. Строки и столбцы, участвующие в образовании базисного минора, так же называются базисными. В курсе алгебры важную роль играет теорема о базисном миноре, которую мы приведем без доказательства.

Теорема: Всякая строка (столбец) матрицы является линейной комбинацией её базисных строк (столбцов).

У матрицы может быть несколько базисных миноров.

Пример: Найти ранг матрицы

A=

Решение: Все миноры 3-го порядка равны 0. Есть минор 2=го порядка отличный от 0 ≠-15. Значит r (A) = 2. Базисный минор стоит на пересечении 2 и 3 строки, c 1 и 3 столбцом.

Отметим свойства ранга матрицы:

1. При транспортировании матрицы её ранг не маняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

Ранг канонической матрицы равен числу единиц на главной диагонали, что используется для вычисления ранга матрицы.

II. Система линейных уравнений.

1. Основные понятия

Системой m линейных алгебраических уравнений с n неизвестными называется система вида:

Здесь a_ij и b_j – произвольные числа (i=1,2,3…m; j=1,2,3…n) которые называются соответственно коэффициентами при неизвестных и свободными членами уравнений.

х_i – неизвестные числа.

Такую систему можно записать более кратко с помощью знаков суммирования.

Или в матричной форме: А × Х = В

Здесь А – матрица коэффициентов системы называемая основной матрицей.

n

X = вектор-столбец у неизвестных x_j; B = вектор-столбец из свободных членов b_i.

Х и В представляют собой векторы столбцы, однако в целях единого подхода в рамках матричной алгебры удобнее трактовать их именно как матрицы состоящие соответственно из n и m строк и одного столбца.

Произведение матрицы А×Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (п – штук).

Расширенной матрицей системы называется матрица Ā системы дополняемая столбцом свободных членов.

Решением системы называется п значений неизвестных x_j=c_j где , при подстановке которых все уравнения системы превращаются в верное равенство (тождество). Всякое решение системы можно записать в виде матрицы-столбца.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Система совместная называется определенной, если она имеет единственное решение, и неопределенной, ели она имеет более одного решения. В последнем случае каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему это, значит, выяснить, совместна она или нет. Если система совместна, то найти её общее решение.

Две системы называются эквивалентными, если они имеют одно и тоже общее решение. Другими словами системы эквивалентны, если каждое решение одной является решением другой и наоборот.

Эквивалентные системы получаются в частности при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

Система линейных уравнений называется однородной, если все свободные члены равны 0.

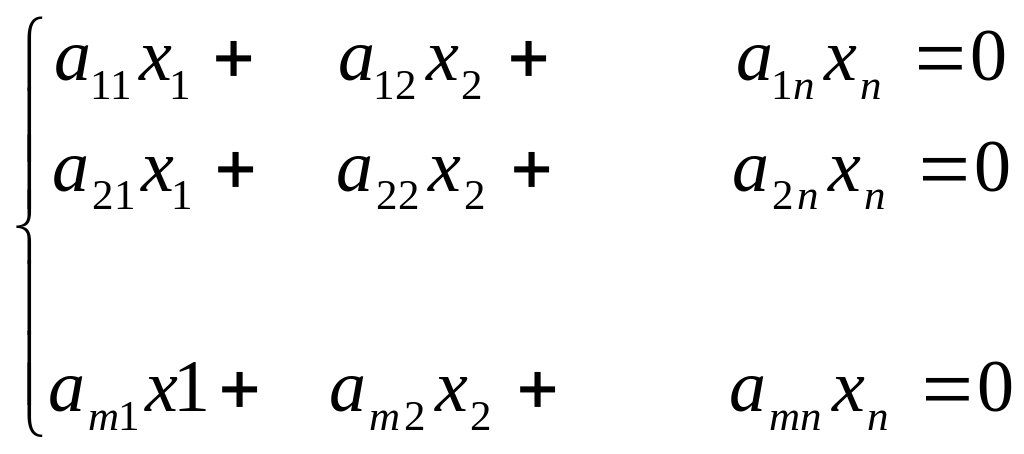
Однородная система всегда совместна так как х₁=х₂…=х_п=0 является решением системы. Это решение называется нулевым или тривиальным.