2. Действия над матрицами

а) Сложение

Операции сложения проводятся только для матриц одинаковых размеров. Суммой двух матриц А_m×n = (a_ij) и B_m×n = (b_ij) называется матрица C_m×n = (c_ij) такая, что c_ij = a_ij + b_ij (i=1…m, j=1…n).

Пример:

+ =

Аналогично производится и вычитание матриц.

б) Умножение на число

Произведение матрицы А_mn=( a_ij ) на число К называется матрица B_m×n=(b_ij) такая, что b_ij=k× a_ij (i=1…m, j=1…n).

Пример:

А= , к=2; А·К=

Матрица – А = (- 1)А называется противоположной матрице А.

Операции сложения и умножения матрицы на число обладают обычным набором арифметических свойств:

1⁰.

2⁰.

3⁰.

4⁰.

5⁰.

6⁰.

7⁰.

8⁰.

Здесь А, В, С- матрицы, а α, β –числа.

в) Элементарные преобразования матриц

Элементарными преобразованиями матриц являются:

• Перестановка двух параллельных рядов матриц

• Умножение всех элементов матрицы на число отличное от нуля

• Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда умноженных на одно и тоже число

Две матрицы называют эквивалентными если одна из них получается из другой с помощью элементарных преобразований, записывается А~В.

При помощи элементарных преобразований любую матрицу можно привести к матрице у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической. Например:

Пример: Привести к каноническому виду А=

г) Произведение матриц

Умножение двух матриц А и В возможно только для случая, когда число столбцов первой матрицы равно числу строк второй (в этом случае матрица А называется согласованной с В). В этом случае произведение матрицы А_m×n=(a_ij) на B_n×p=(b_jk) называется матрица C_m×p=(c_ik) такая, что c_ik =a_i1b_1k+a_i2b_2k+…+a_inb_nk , ( i=1…m, k=1…p).

Т.е. элемент i строки и k-го столбца матрицы С, равен сумме произведений элементов i-й строки А на соответствующие элементы k-го столбца В.

Пример: =

Для умножения матриц справедливы еще четыре арифметические операции:

1.) 2.)

3.) 4.)

Для операции транспортирования верны свойства:

1.) (А+В)^Т = А^Т + В^Т 2.) ( )^Т =

2. Определители

1. Основные понятия

При решении систем уравнений, о которых мы будем говорить позже, необходимо ввести понятие определителя – числа сопоставляемого с квадратной матрицей А. Обозначается определитель так - |A|, ∆ или det A. Сопоставление должно происходить следующим образом:

а. Матрица порядка n=1, A = ( ₁), det A = ₁

б. n=2 A= detA= = _{11 22}- _{12 21.}

в.n=3 A= ;

detA= = .

При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (Саррюса).

=

2. Свойства определителей (необходимы для вычисления определителей):

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

= :

=

В дальнейшем строки и столбцы будем называть просто рядами.

2. При перестановке двух параллельных рядов определитель меняет знак.

3. Определитель, имеющий два одинаковых ряда равен нулю.

4. Общий множитель элементов, какого – то ряда определителя можно вынести за знак определителя.

Из свойств 3) и 4) следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

Пример:

= =K·0=0

5. Если элементы какого либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Пример:

= +

6. Определитель не изменится если к элементам одного ряда прибавить соответствующие элементы параллельного ряда умноженные на любое число.

Пример:

= =

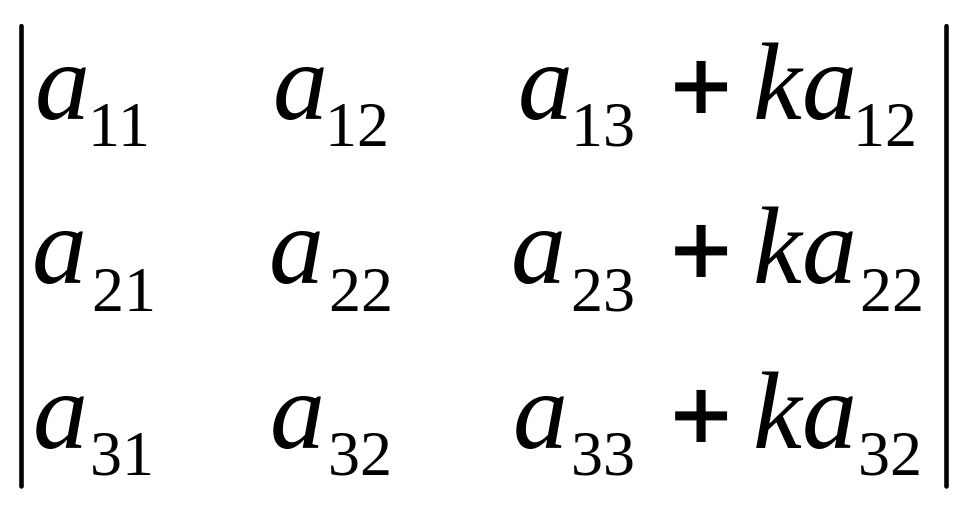Используя 3),4) и 5) получим ∆=

= + k=∆+ =∆

7. Теорема Лапласа: (Разложение определителя по элементам некоторого ряда). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения. Для того чтобы понять, что такое алгебраическое дополнение необходимо ввести понятие минора. Минором некоторого элемента a_ij определителя n –го порядка называется определитель n-1-го порядка полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится данный элемент, обозначается m_ij.

Так если: ∆= , то m₁₁= ; m₃₂=

Алгебраическим дополнением элемента a_ij определителя называется его минор взятый со знаком «+» если сумма i+j – четное число, и со знаком «-» если сумма нечетная. Обозначается А_ij

A_ij =(-1)^i+jm_ij, так A₁₁=+m₁₁, A₃₂=-m₃₂

Теперь вернемся к свойству 7) согласно определения для определителя∆ 3-го порядка

∆= =

Доказательство

-a₁₂ +a₁₃ =

= ∆

Последнее свойство используется для вычисления определителей высокого порядка.

8. Сумма произведений элементов, какого либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равно 0.

Пример: a₁₁A₂₁+a₁₂A₂₂+a₁₃A₂₃=0.