3.4.Переход к новому базису.

Пусть B=( ) и B'=( ) старый и новый базисы линейного векторного пространства Rⁿ. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:

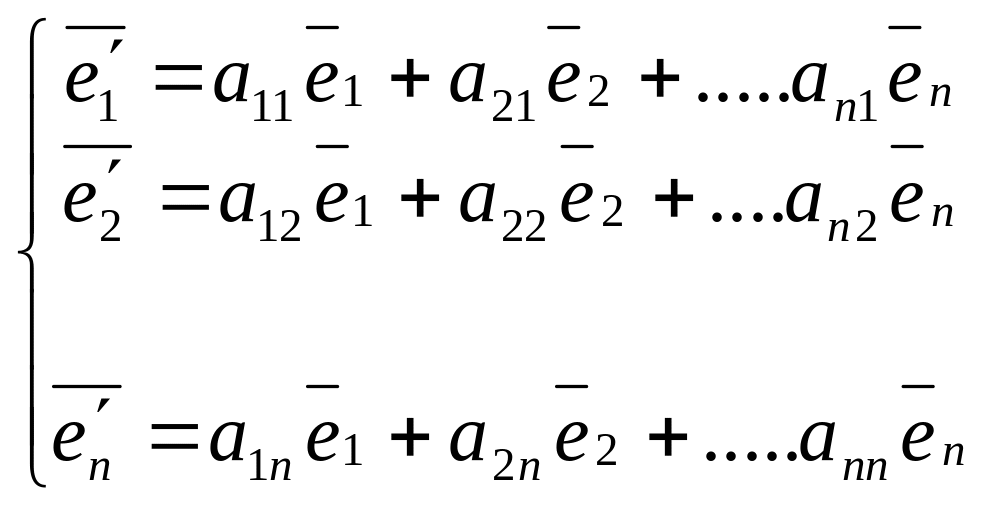
Или

Или в сокращенной матричной форме:

,где

T - называется матрицей перехода от старого базиса к новому . Следует обратить внимание на то, что координаты разложения нового базиса по старому базису располагаются в матрице перехода по столбцам. Матрица перехода от нового базиса к старому имеет вид:

T^-1; B =B′ ·T^-1;

Найдем зависимость между координатами вектора в разных базисах. Пусть некоторый вектор имеет координаты (x₁ x₂ …х_n) в старом и (x'₁, x'₂,...x'_n) в новом, тогда

Подставив сюда разложение векторов ( ) по базису( ),получим:

+

Перенесем все влево и сгруппируем слагаемые с одинаковыми сомножителями

Это равенство выполняется при условии, что все коэффициенты перед равны 0. следовательно:

Или в матричной форме:

или X=TX¹

3.5. Линейные операторы.

Пусть Rⁿ₁ R^m₂-линейные пространства размерности n и m. Если задан закон (правило),по которому каждому вектору x пространства Rⁿ₁ ставится в соответствии единственный вектор y пространства R^m₂, то говорят, что задан оператор действующий из Rⁿ₁ в R^m₂ и записывают эту операцию . Оператор называется линейным, если для любых векторов x и y пространства Rⁿ и любого числа λ выполняются соотношения:

1)

2)

Вектор -называется образом вектора ,а сам вектор –прообразом вектора .

Если пространства Rⁿ₁ и R ^m ₂ совпадают, то оператор отображает пространство Rⁿ₁ в себя. Именно такие операторы мы и будем рассматривать.

Пусть в пространстве Rⁿ задан базис( ₁, ₂,.. _n).Произвольный вектор может быть разложен по этому базису:

Выясним, что собой представляет оператор , для этого подействуем на вектор оператором :

Поскольку (i=1,2..n) является вектором Rⁿ то их также можно разложить по базису ( ₁, ₂,.. _n):

и тогда

(1)

С дpугой стороны по определению, есть некоторый вектор , и имеет в том же базисе ( ₁, ₂,.. _n), координаты y₁,y₂...y_n и поэтому он может быть разложен по этому базису:

(2)

Разложение вектора по базису единственно, поэтому правые части (1) и (2) равны следовательно:

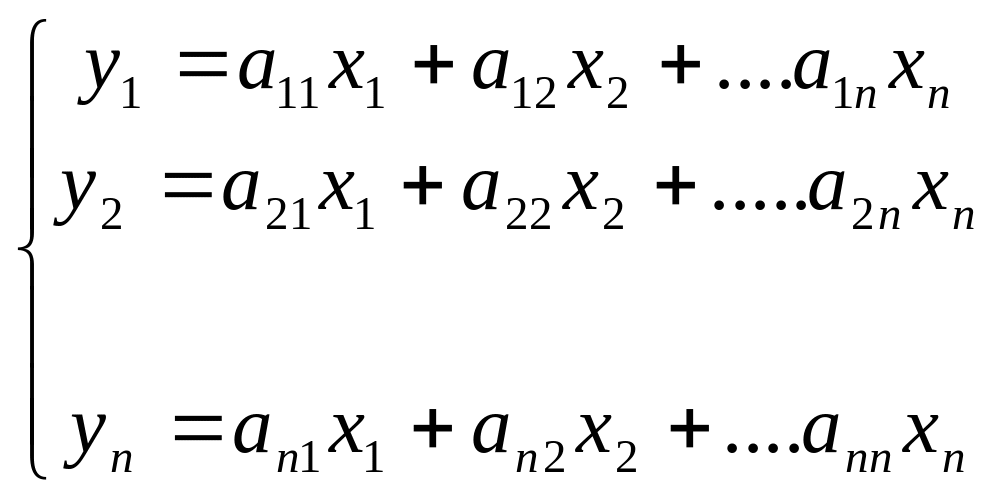
Или в матричной форме

Таким образом, действие линейного оператора на вектор сводится к умножению некоторой матрицы P=( _ij) на матрицу столбец, составленный из координат вектора . Матрица P называется матрицей линейного оператора в базисе ( ₁, ₂,.. _n), а ранг матрицы рангом оператора . Таким образом, каждому линейному оператору соответствует матрица в данном базисе и наоборот.

Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой .

Теорема1. матрицы P и P' линейного оператора ,в старом базисе ( ₁, ₂,.. _n) и новом связаны соотношениями:

, где Т – матрица перехода от старого базиса к новому.

Теорема2. Определитель матрицы линейного оператора не зависит от выбора базиса.