85

Государственное образовательное учреждение

Высшего профессионального образования Тюменской области

ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ

МИРОВОЙ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА

Кафедра математики, информатики и естественных наук

Р.М. Султанаев

Высшая математика

Курс лекций

для студентов всех специальностей

очной и заочной форм обучения

( ЧАСТЬ 1 )

Тюмень, 2009

Часть I Введение

Математика одна из самых древних наук и появилась в связи с необходимостью количественных расчетов в окружающем человека мире. Наиболее простейший расчет – определение хотя бы числа пальцев на руке, количество добытой дичи и т.п. По мере развития общества появилась необходимость во все более сложной системе расчетов, обусловленных зарождаемым строительством, торговлей и, например, морским плаванием.

Статус самостоятельной науки математика приобрела в древней Греции и Китае еще до нашей эры. Все философские школы того времени включали математику в круг вопросов миросозерцания.

Важнейший вклад в появление математики, как самостоятельной науки, внесли работы Евклида, Архимеда и Аристотеля. Так Евклид в своих «началах» заложил основы классической геометрии, а Архимед в малоизвестных работах разрабатывал «азы» дифференциального и интегрального счисления и теории бесконечно малых величин. Последние работы были заново выполнены только в 16-18 веках н.э. Все это привело к появлению математики переменных величин. На первый план выдвигаются понятия функции, играющие в дальнейшем такую же роль основного и самостоятельного предмета изучения как ранее известные понятия числа и величины. Именно исследование функциональных зависимостей, их описание приводит к созданию математического анализа. В дальнейшем благодаря Декарту установилась связь между геометрией и алгеброй и открылась возможность геометрической интерпретации алгебраических и аналитических данных.

Математика, как система различного рода количественных расчетов и функциональных зависимостей, используется всеми без исключения современными науками. Можно сказать, что без математики невозможно существование никакой современной науки.

Надо отметить, что новые направления в математике возникают, не только в результате запросов естественных наук, но и вследствие внутренней потребности самой математики как науки. Примером тому является неэвклидова (Риманова) геометрия, разработанная в трудах Лобачевского и Римана.

Новый толчок в развитии математики появился в связи с созданием вычислительных машин. С их появлением появилась возможность приблизительного расчета, с требуемой точностью, количественных характеристик самых различных явлений в окружающем нас микро и макро мире. Особенно большое влияние появление ЭВМ оказало на исследование явлений и процессов описываемых путем математического моделирования.

Аналитическое решение применительно к сложным математическим моделям оказывалось почти всегда невозможным, а с помощью ЭВМ, возможно, получить результат с достаточной точностью.

Точно такой же подход используется экономистами для развития наших представлений об экономиках различных типов.

I. Линейная алгебра.

I. Матрицы.

1. Основные понятия.

Понятие матрицы и основанный на нем раздел математики – матричная алгебра имеет большое значение для экономистов. Дело в том, что большая часть математических моделей используемых при описании экономических процессов записывается в матричной форме.

Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк одинаковой длины n – столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрица записывается в виде:

A=

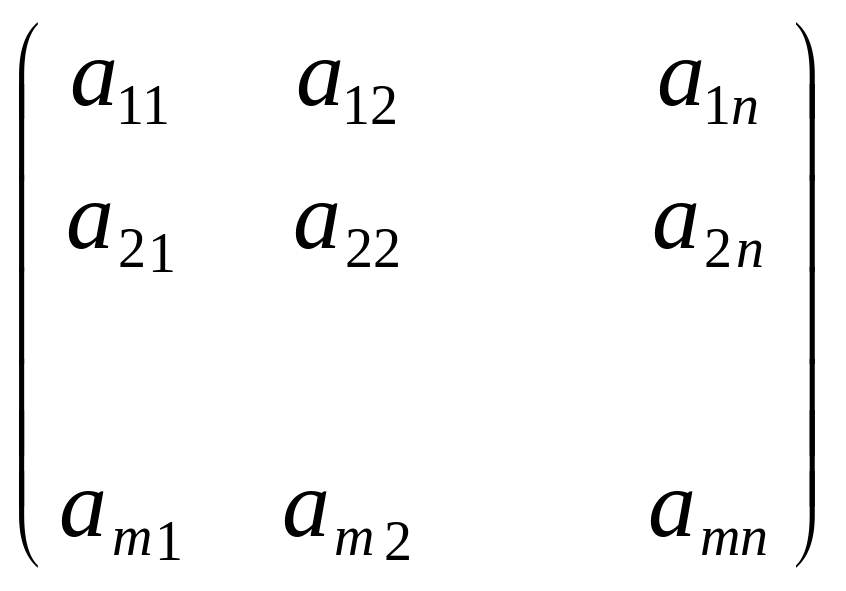
Или сокращенно А =(a_ij) , где i = 1, m (т.е. i=1,2,…m) – номер строки, j=1, n (т.е. j=1,2,3,…n) – номер столбца. Матрицу А называют матрицей размера m×n и пишут Am×n. Элементы, стоящие на диагонали идущей из верхнего угла образуют главную диагональ.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т.е. А = В, если a _ij = b _ij, где i = 1…m, j = 1…n.

Матрица, у которой число строк равно числу столбцов называется квадратной. Квадратную матрицу размера n×п называют матрицей n- порядка.

Квадратная матрица, у которой все элементы кроме элементов главной диагонали равны нулю, называется – диагональной.

Диагональная матрица, у которой каждый элемент равен единице, называется единичной. Обозначают буквой Е.

Пример: Е _3х3= 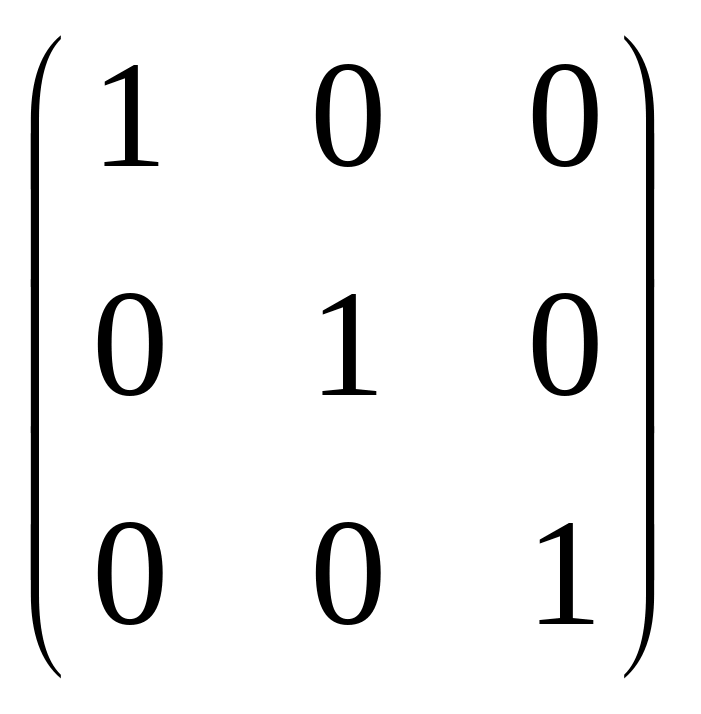- единичная матрица 3^-его порядка

П ример: Е _nхn= 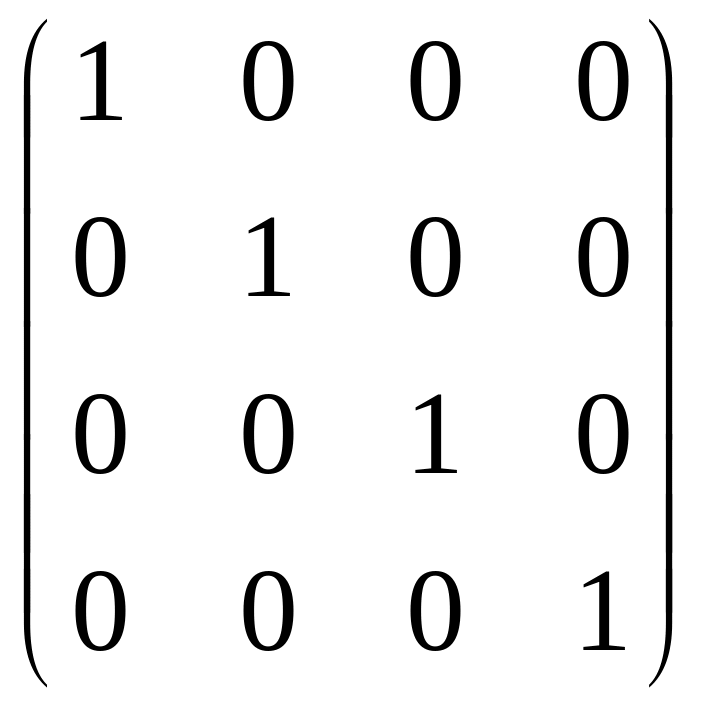–единичная матрица n^-го порядка

Квадратная матрица называется треугольной если все элементы, расположенные по одну сторону от главной диагонали равны 0 (нулю).

Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О, Имеет Вид:

О =

В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике. Матрицу, содержащую один столбец или одну строку, называют вектором (или вектор – столбец или вектор – строка соответственно). Их вид:

А= или B=

Матрица размера 1×1, состоящая из одного числа отождествляется с этим числом т.е. ( 5 )_1×1 = 5.

Матрица, полученная из данной, заменой каждой её строки столбцом с тем же номером, называется транспонированной к данной. Обозначается А^Т

Так если А= , то А^Т= , если А= , то А^Т=

Транспонированная матрица обладает следующим свойством: (А^Т)^Т = А