2.4. Движение материальной точки в однородном силовом поле

Силовым полем называется пространство, в каждой точке которого на помещенную в нее материальную точку действует некоторая сила. В общем случае эта сила зависит от положения материальной точки в силовом поле и от времени, т.е.

.

Если сила не зависит явно от времени, то силовое поле называется стационарным. Если сила, действующая со стороны силового поля на материальную точку, не зависит от положения материальной точки в силовом поле, то такое силовое поле называется однородным. Отметим, что однородное силовое поле является стационарным. В таком поле

. (2.21)

Рассмотрим движение материальной точки в однородном силовом поле.

На основании второго закона Ньютона (2.8) (в системе единиц СИ k=1) имеем:

, (2.22)

где в силу условия (2.21) - постоянное по величине и направлению ускорение материальной точки.

Пусть в некоторый момент времени t₀, условно принятый за начальный, материальная точка имела относительно выбранной инерциальной системы отсчета скорость . Удобно в этом случае оси координат ориентировать, используя направления и . Направим ось ОY вдоль вектора , а плоскость XОY совместим с плоскостью, в которой лежат векторы и (рис. 2.5).

При таком выборе системы координат

(2.23)

Используя определение ускорения , для приращения скорости за время dt получим

.

y

t₀

m

y₀

x

x₀

0

z

Рис. 2.5

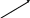
Интегрируя последнее соотношение

,

будем иметь

или

(2.24)

Из определения скорости материальной точки (1.5) элементарный вектор перемещения за время равен . Поэтому с учетом (2.24) и интегрирования

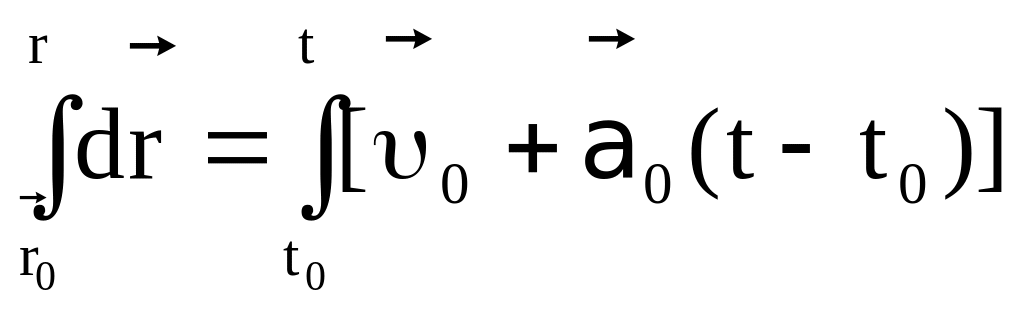
получим

(2.25)

Движение материальной точки в однородном силовом поле полностью описывается кинематическим уравнением движения (2.25) и зависимостью скорости от времени t (2.24). Эти уравнения в выбранной системе координат с учетом (2.23), соответственно, примут вид

(2.26)

Из уравнений (2.26) и (2.27) видно, что движение материальной точки происходит в одной плоскости XОY и по характеру вдоль оси ОX

(2.27)

является равномерным ( ), вдоль оси ОY - равнопере-менным.

Из уравнений (2.26) можно получить уравнение траектории материальной точки. Для этого исключим из них время t:

(2.28)

Полученное выражение представляет собой уравнение параболы. Реальное движение, естественно, ограничено во времени и в пространстве, поэтому физический смысл имеет только конкретный участок параболы (2.28).

Примерами движения материальной точки в однородном силовом поле являются :

- движение частицы вблизи поверхности Земли под действием силы тяжести (h << R_з). В этом случае = ;

- движение заряженной частицы в однородном электростатическом поле. В этом случае

Выводы: В однородном силовом поле материальная точка движется с постоянным ускорением. Траекторией движения точки является ветвь параболы.