3.8.3. Роль закона сохранения механической энергии при решении конкретных задач

Чтобы проиллюстрировать те огромные преимущества, которые дает во многих случаях применение закона сохранения энергии при решении конкретных практических задач, полезно, по мнению автора, рассмотреть решение “очень простой”, на первый взгляд задачи:

Пусть материальная точка m “свободно” вращается в вертикальной плоскости по окружности радиуса R (камень на легкой нерастяжимой веревке). При прохождении верхнего положения скорость частицы . Определить скорость частицы при прохождении ею нижнего положения.

Под “свободным” здесь понимается движение частицы под действием двух сил: силы тяжести и силы натяжения веревки .

а) Попытаемся вначале хотя бы представить ход решения этой задачи на основе применения законов Ньютона (рис.3.11).

Уравнение движения частицы имеет вид

или в проекциях на радиальное и касательное направления:

m

t=0





0

R

t₂

Рис. 3.11

Смысл обозначений ясен из рисунка.

Второе из этих уравнений определяет силу натяжения N и “закон” ее изменения при вращении частицы, поэтому в дальнейшем мы его рассматривать не будем.

Первое уравнение можно преобразовать к одной неизвестной функции времени с помощью после чего получим:

.

К сожалению , несмотря на “простой” вид этого уравнения математически можно решать такое уравнение только приближенно, численными методами. Однако проследить дальнейший ход рассуждений достаточно просто. Предположим, что нам удалось каким-либо методом найти зависимость угла

как функцию времени, то есть .Тогда для момента времени t₂ при прохождении частицей нижнего положения будем иметь

и

Определив t₂ из первого равенства и подставив во второе, найдем искомое значение скорости ;

б) Решение этой задачи с помощью закона сохранения механической энергии точно и записывается одной строкой.

Сила тяжести потенциальна, а сила натяжения перпендикулярна скорости частицы, поэтому полная механическая энергия частицы сохраняется. В нижнем положении частицы ее потенциальная энергия в поле силы тяжести принята равной нулю, то есть . Записав равенство механической энергии для верхнего и нижнего положений

,

имеем значение искомой величины:

Комментарии излишни.

9. Закон сохранения момента импульса

Задачей этого пункта является поиск третьей аддитивной сохраняющейся величины - интеграла движения. Как и пункте 3.2, рассмотрим произвольную систему N материальных точек. Исходные уравнения движения частиц системы имеют тот же вид

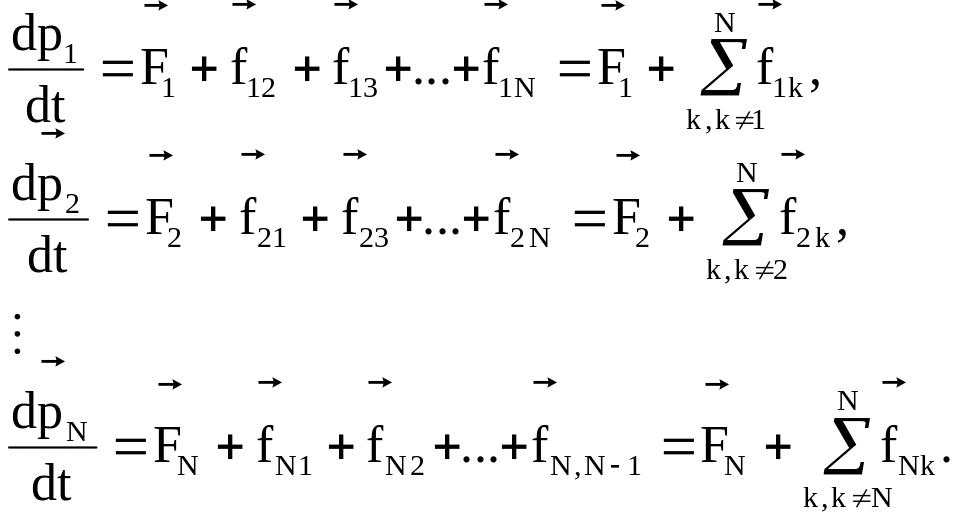
Умножим векторно каждое из этих уравнений почленно слева на соответствующий радиус-вектор положения частицы в выбранной системе отсчета:

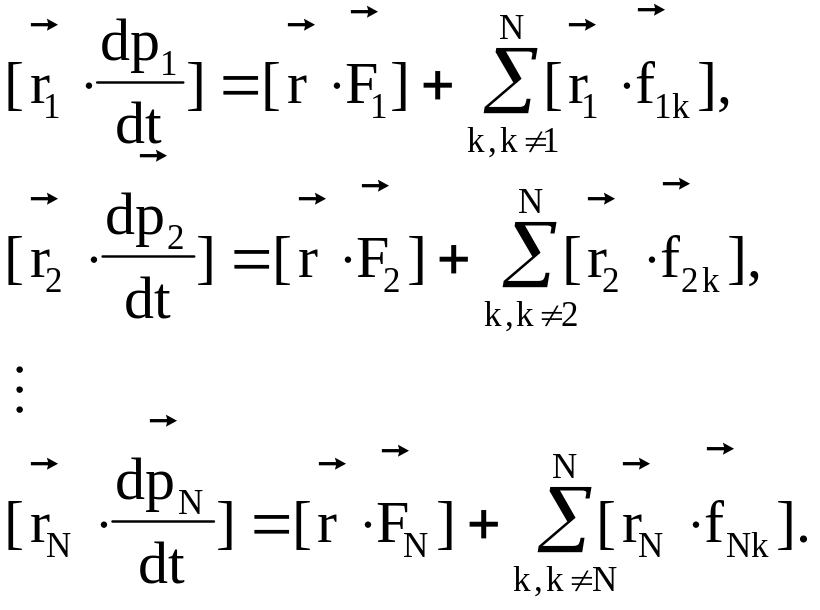
Легко видеть, что

Так как , то

В соответствии с этим равенством уравнения движения частиц системы примут вид

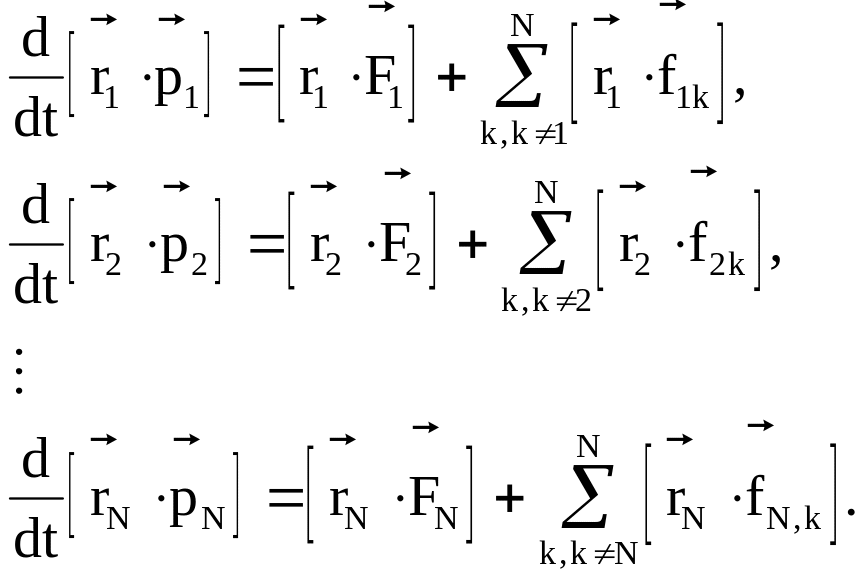(3.46)

Введем определения и обозначения:

а) Векторное произведение радиус-вектора материальной точки на вектор ее импульса называется моментом импульса частицы относительно точки, выбранной за начало системы отсчета:

(3.47)

б) Векторное произведение радиус-вектора материальной точки на вектор силы, действующей на эту точку, называется моментом силы относительно точки, выбранной за начало системы отсчета:

(3.48)

Обсуждение свойств и смысла величин и будет сделано ниже.

Сложим почленно уравнения системы (3.46) с учетом введенных определений (3.47) и (3.48):

(3.49)

Покажем, что последняя сумма в правой части равенства (3.49) равна нулю. Действительно, в этой сумме попарно присутствуют слагаемые вида

i

k

0

Рис. 3.12

Справедливость этого равенства ясна из рис. 3.12, где учтено, что - силы взаимодействия частиц i и k, а .

С учетом сказанного, равенство (3.49) примет вид

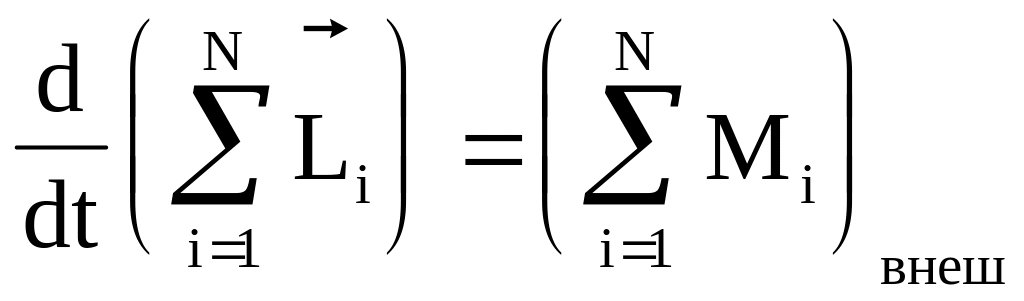. (3.50)

Определения:

- векторная сумма моментов импульсов частиц системы называется моментом импульса системы материальных точек:

(3.51)

Как видно из этого определения, момент импульса системы материальных точек является аддитивной величиной;

- векторная сумма моментов сил, вообще говоря, не является результирующим моментом всех сил, поэтому сумму

(3.52)

в общем случае нельзя заменить эквивалентным моментом одной силы.

С учетом (3.51) и (3.52) равенство (3.50) примет вид

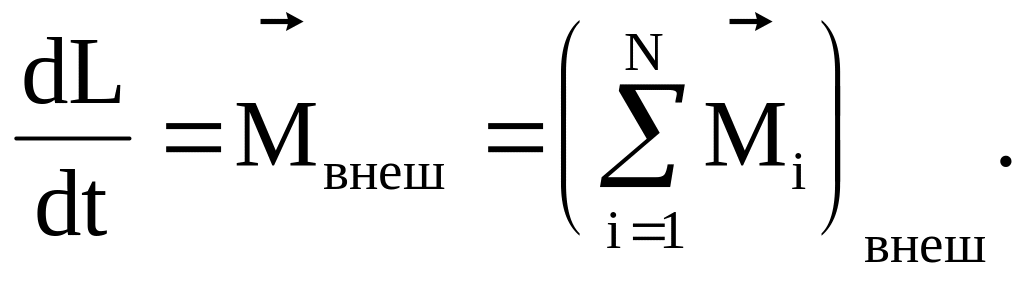(3.53)

Оно называется уравнением моментов и устанавливает тот факт, что момент импульса системы материальных точек может измениться только в результате действия внешних моментов сил.

Скорость изменения момента импульса системы равна векторной сумме моментов всех внешних сил, действующих на систему.

Если сумма моментов внешних сил, действующих на систему, равна нулю, то момент импульса системы остается постоянным

. (3.54)

Последнее утверждение называется законом сохранения момента импульса системы.

В частности, момент импульса замкнутой системы (все ) тоже сохраняется. Обратите внимание на аналогичный вид равенств (3.3) и (3.53).

Вывод: Итак, при условиях, когда суммарный момент внешних сил, действующих на систему частиц, равен нулю, найдена третья сохраняющаяся аддитивная величина (интеграл движения), которой является момент импульса системы частиц.

Контрольные вопросы.

3.12. Какое условие должно выполняться, чтобы сохранялась проекция момента импульса на некоторое направление?