
- •Часть I
- •Кинематика
- •1.1. Основные вопросы механики
- •1.2. Основные физические модели и понятия механики
- •1.3. Кинематика материальной точки
- •1.3.1. Система отсчета
- •1.3.2. Радиус-вектор, вектор перемещения
- •1.3.6. Взаимосвязь между линейными и угловыми кинематическими величинами
- •1.4. Кинематическое уравнение движения. Прямая и обратная задачи кинематики
- •Кинематика твердого тела
- •2. Динамика материальной точки
- •2.1. Ньютоновская динамика и границы ее применимости
- •2.2. Законы Ньютона
- •2.3. Силы
- •2.3.1. Гравитационное взаимодействие
- •2.3.2. Электромагнитное взаимодействие
- •2.4. Движение материальной точки в однородном силовом поле
- •Законы сохранения в механике
- •3.1. Интегралы движения и законы сохранения
- •3.2.Закон сохранения импульса и его векторный характер
- •3.3. Механическая работа
- •3.4. Кинетическая энергия
- •3.5. Потенциальная энергия и ее связь с силой
- •Поле сил тяготения и кулоновское силовое поле
- •3.6.3. Поле силы тяжести
- •3.6.4. Поле упругих сил
- •3.7. Закон сохранения механической энергии
- •3.8. Примеры применения законов сохранения механической энергии и импульса
- •Движение частицы в потенциальном силовом поле
- •3.8.2. Абсолютно упругий удар двух материальных точек
- •3.8.3. Роль закона сохранения механической энергии при решении конкретных задач
- •Закон сохранения момента импульса
- •3.10. Момент силы. Момент импульса
- •Элементы динамики вращательного движения твердого тела
- •Вращение твердого тела относительно неподвижной оси
- •4.2. Момент инерции
- •4.3. Примеры вычисления моментов инерции однородных симметричных тел
- •4.4. Кинетическая энергия вращающегося твердого тела
- •Механическая работа при вращательном движении твердого тела
- •4.6. Сравнение описаний движения материальной точки и вращения твердого тела
- •Применение основных законов динамики твердого тела при решении конкретных задач
- •5. Основы специальной теории относительности (сто)
- •5.1. Преобразования Галилея. Принцип относительности Галилея
- •Любая система отсчета , движущаяся относительно некоторой инерциальной системы отсчета равномерно и прямолинейно, также является инерциальной.
- •5.2. Опыт Майкельсона. Постулаты теории относительности
- •Принцип постоянства (инвариантности) скорости света
- •5.3. Преобразования Лоренца
- •5.4. Следствия из преобразований Лоренца
- •5.4.1. Лоренцовское сокращение длины
- •5.4.2. Относительность промежутков времени
- •5.4.3. Относительность одновременности
- •5.5. Релятивистский закон сложения скоростей
- •5.6. Релятивистские импульс и масса частицы
- •5.7. Релятивистская энергия
- •1. Релятивистская кинетическая энергия частицы определяется приращением ее полной энергии (5.23), (5.26).
- •2. Полная энергия системы и ее масса связаны универсальной формулой а. Эйнштейна (5.28).
- •5.8. Связь релятивистской энергии и импульса частицы
- •6. Ответы на контрольные вопросы
- •Кинематика
- •Динамика материальной точки
- •Законы сохранения в механике
- •Элементы динамики вращательного движения твердого тела
- •Основы специальной теории относительности
- •Оглавление
- •Уколов Александр Сергеевич
- •Часть 1
2.3.2. Электромагнитное взаимодействие
В
основе описания электромагнитного
взаимодействия лежит фундаментальный
закон Кулона,
определяющий силу взаимодействия двух
точечных заряженных частиц, неподвижных
или движущихся с относительной скоростью
![]() :
:
![]() ,
(2.16)
,
(2.16)
где q1 и q2 - заряды частиц, k - коэффициент пропорциональности, зависящий от выбора системы единиц (в системе СИ k = 9109 м/Ф). Замечания по поводу применения закона Кулона подобны замечаниям к применению закона всемирного тяготения.
Так как в природе существуют заряды двух знаков, то силы кулоновского взаимодействия могут иметь как характер притяжения, так и отталкивания.
Для примера сравним величины силы гравитационного притяжения и силы кулоновского отталкивания двух электронов.
Так как
![]() ,
,
![]() ,
,
то
![]() .
.
Учтя
значения величин
![]() Кл,
Кл,
![]() кг, получим
кг, получим
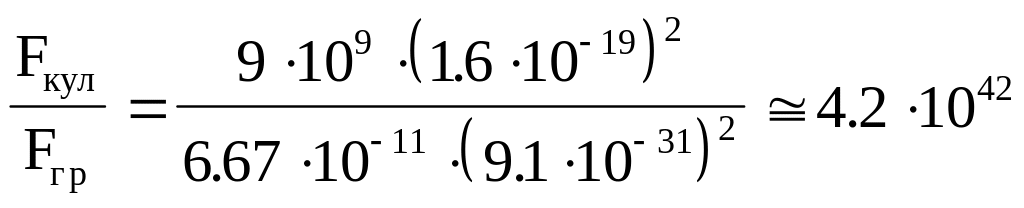 .
.
Таким
образом, кулоновское отталкивание![]() превышает
гравитационное притяжение между двумя
электронами более чем в 1042
раз.
превышает
гравитационное притяжение между двумя
электронами более чем в 1042
раз.
Кулоновское взаимодействие между заряженными частицами передается посредством электромагнитного поля, которое может существовать как самостоятельный материальный объект.
Свойства
электромагнитного поля описываются
напряженностью
![]() его электрической компоненты и индукцией
его электрической компоненты и индукцией
![]() магнитной компоненты.
магнитной компоненты.
В огромном числе случаев приходится рассматривать движение заряженной частицы во внешних электромагнитных полях. В этих ситуациях на заряженную частицу со стороны электромагнитного поля действует фундаментальная сила:
![]() ,
(2.17)
,
(2.17)
которая называется силой
Лоренца. Эта сила,
как видно из (2.17), имеет две естественные
![]()
![]() -
электрическую и
-
электрическую и
![]() -
магнитную составляющие. Выражение
(2.17) для силы Лоренца применимо не только
в классической, но в квантовой механике.
-
магнитную составляющие. Выражение
(2.17) для силы Лоренца применимо не только
в классической, но в квантовой механике.
Рассмотрим два важных случая проявления электромагнитного взаимодействия между очень большим числом частиц.
Сила упругости
Из опыта известно, что если
на любое реальное тело подействовать
силой, то, в зависимости от свойств этого
тела, оно изменяет свои форму и размеры,
то есть деформируется.
Деформация тела называется упругой,
если после прекращения действия силы
тело полностью восстанавливает свои
прежние размеры и форму. В этом случае
сила, возникающая со стороны деформируемого
тела, оказывается прямо пропорциональной
величине деформации
![]()
и направлена в сторону, обратную
деформации тела:
и направлена в сторону, обратную
деформации тела:
![]() ,
(2.18)
,
(2.18)
где коэффициент пропорциональности k называется коэффициентом упругости (жесткости). Соотношение (2.18) является математическим выражением опытного закона Гука.
Электромагнитную природу упругой силы можно объяснить следующими рассуждениями.
F
F>0
r0
r
F<0
Рис. 2.3.




Рис. 2.3 качественно отображает зависимость силы взаимодействия F между двумя частицами в теле от величины среднего расстояния между ними (r0-среднее равновесное расстояние между частицами). При попытке сжать тело расстояние между частицами уменьшается (r < r0) и взаимодействие между ними приобретает характер отталкивания (F>0); при растяжении тела (r > r0) взаимодействие имеет характер притяжения . При небольших смещениях частиц друг относительно друга | r-r0 | << r0 из рис. 2.3 видно, что
![]() ,
,
т.е. сила взаимодействия между двумя частицами пропорциональна их смещению друг относительно друга.
Это непосредственно объясняет справедливость закона Гука.
Здесь следует отметить, что в предельных случаях, когда деформациями взаимодействующих между собой тел можно пренебречь, силы упругости проявляются в виде реакции опоры, силы натяжения и т.д.
Часто действие одной или нескольких сил на материальную точку или тело не связано ни с какими деформациями, но количественно подчиняется соотношению (2.18). В этих случаях соответствующие силы называются квазиупругими.
Контактные силы
Взаимодействие двух тел при
их непосредственном контакте, когда
поверхности тел соприкасаются между
собой, обладают весьма своеобразном
характером. Это проявляется в том, что
величина и направление контактных сил
существенным образом зависят от характера
относительного движения контактирующих
тел. С другой стороны, сам характер
относительного движения зависит от сил
взаимодействия между контактирующими
телами. Чтобы разрешить возникающее
противоречие, вводят вместо одной
реальной контактной силы взаимодействия
ее две составляющие, одна из которых
направлена перпендикулярно соприкасающимся
поверхностям взаимодействующих тел,
другая - по касательной к этим поверхностям.
Перпендикулярная составляющая называется
реакцией опоры
,
касательная -
силой трения ![]() .
Из-за важной роли, которую эти составляющие
играют в определении характера
относительного движения контактирующих
тел, реакция опоры и сила трения стали
иметь значения самостоятельных “сил”.
При этом, конечно, необходимо ясно
понимать, что сила реакции опоры и сила
трения - всего лишь составляющие реальной
контактной силы взаимодействия между
двумя телами.
.
Из-за важной роли, которую эти составляющие
играют в определении характера
относительного движения контактирующих
тел, реакция опоры и сила трения стали
иметь значения самостоятельных “сил”.
При этом, конечно, необходимо ясно
понимать, что сила реакции опоры и сила
трения - всего лишь составляющие реальной
контактной силы взаимодействия между
двумя телами.
Для пояснения своеобразия контактной силы взаимодействия между двумя телами рассмотрим следующий мысленный эксперимент.
0
а б
в Рис 2.4![]()

![]()
![]()
![]()
![]()

![]()
![]()



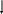




![]()
Его состояние в этом случае
определяется действием двух сил: силы
тяжести
и контактной силы
.
Так как брусок находится в равновесии,
то
![]() ,
и
перпендикулярна горизонтальной
поверхности. Поэтому в этом состоянии
сила
имеет только одну составляющую - реакцию
опоры (
,
и
перпендикулярна горизонтальной
поверхности. Поэтому в этом состоянии
сила
имеет только одну составляющую - реакцию
опоры (![]() ),
вторая составляющая, сила трения, равна
нулю.
),
вторая составляющая, сила трения, равна
нулю.
Попытаемся теперь, приложив
к бруску горизонтальную внешнюю силу
![]() ,
сдвинуть брусок относительно опоры
(рис. 2.4, б). Если посте-пенно увеличивать
величину
от нуля до некоторого предельного
значения
,
сдвинуть брусок относительно опоры
(рис. 2.4, б). Если посте-пенно увеличивать
величину
от нуля до некоторого предельного
значения
![]() ,
то брусок будет находиться в состоянии
покоя относительно горизонтальной
поверхности. Это означает, что у силы
появится горизонтальная составляющая
,
то брусок будет находиться в состоянии
покоя относительно горизонтальной
поверхности. Это означает, что у силы
появится горизонтальная составляющая
![]() направленная противоположно
направленная противоположно
![]() ,
величина которой автоматически
подстраивается так, чтобы выполнялось
равенство
,
величина которой автоматически
подстраивается так, чтобы выполнялось
равенство
![]() ,
,
![]() .
.
В этом случае
![]() называется силой
трения покоя.
называется силой
трения покоя.
При дальнейшем увеличении
внешней силы Fвнеш.
> F0
брусок начинает скользить относительно
горизонтальной поверхности. Если
относительная скорость сравнительно
невелика, то величина и направление
контактной силы
,
а значит и ее составляющая
![]() ,
перестают изменяться. При этом между
величинами составляющих
и
,
перестают изменяться. При этом между
величинами составляющих
и
![]() устанавливается постоянное соотношение:
устанавливается постоянное соотношение:
![]() (2.19)
(2.19)
где
![]() =
const называется коэффициентом
трения скольжения,
а Fтр. -
силой трения скольжения.
Величина
существенным образом зависит от многих
факторов, таких, как свойства контактирующих
материалов, обработки поверхностей, их
чистоты и т.д.
=
const называется коэффициентом
трения скольжения,
а Fтр. -
силой трения скольжения.
Величина
существенным образом зависит от многих
факторов, таких, как свойства контактирующих
материалов, обработки поверхностей, их
чистоты и т.д.
При изменении направления внешней силы на противоположное, сила трения также меняет свое направление на противоположное. Поэтому сила трения всегда направлена в сторону, противоположную относительному движению или попытке вызвать такое движение.
Контактные силы имеют электромагнитную природу и обусловлены взаимодействием частиц, находящихся в приповерхностных слоях контактирующих тел.
При движении тела в жидкости или газе возникает сила сопротивле-
ния, направленная в сторону, противоположную относительному движению, и при малых скоростях пропорциональная этой скорости, то есть
![]() .
(2.20)
.
(2.20)
Коэффициент в (2.20) зависит от вязкости жидкости и размеров тела. Соотношение (2.20) справедливо, если жидкость обтекает тело слоисто, без завихрений.
Выводы: В классической механике все силы имеют либо гравитационную, либо электромагнитную природу. Проявлением этих сил являются сила тяжести, вес тела, силы упругости, силы трения и сопротивления, и т.д.
Контрольные вопросы.
2.2. Определите, в каком количественном соотношении должны находиться массы и заряды двух совершенно одинаковых частиц, чтобы гравитационное притяжение уравновешивалось кулоновским отталкиванием?
2.3. Покажите, что на материальную точку, подвешенную на нерастяжимой нити, при ее малом отклонении от положения равновесия, действует результирующая сил тяжести и натяжения, которая имеет квазиупругий характер.
2.4. Определите зависимость силы трения, действующей на брусок, находящейся на наклонной плоскости, от ее угла наклона (считайте коэффициент трения скольжения известным).
