
- •Часть I
- •Кинематика
- •1.1. Основные вопросы механики
- •1.2. Основные физические модели и понятия механики
- •1.3. Кинематика материальной точки
- •1.3.1. Система отсчета
- •1.3.2. Радиус-вектор, вектор перемещения
- •1.3.6. Взаимосвязь между линейными и угловыми кинематическими величинами
- •1.4. Кинематическое уравнение движения. Прямая и обратная задачи кинематики
- •Кинематика твердого тела
- •2. Динамика материальной точки
- •2.1. Ньютоновская динамика и границы ее применимости
- •2.2. Законы Ньютона
- •2.3. Силы
- •2.3.1. Гравитационное взаимодействие
- •2.3.2. Электромагнитное взаимодействие
- •2.4. Движение материальной точки в однородном силовом поле
- •Законы сохранения в механике
- •3.1. Интегралы движения и законы сохранения
- •3.2.Закон сохранения импульса и его векторный характер
- •3.3. Механическая работа
- •3.4. Кинетическая энергия
- •3.5. Потенциальная энергия и ее связь с силой
- •Поле сил тяготения и кулоновское силовое поле
- •3.6.3. Поле силы тяжести
- •3.6.4. Поле упругих сил
- •3.7. Закон сохранения механической энергии
- •3.8. Примеры применения законов сохранения механической энергии и импульса
- •Движение частицы в потенциальном силовом поле
- •3.8.2. Абсолютно упругий удар двух материальных точек
- •3.8.3. Роль закона сохранения механической энергии при решении конкретных задач
- •Закон сохранения момента импульса
- •3.10. Момент силы. Момент импульса
- •Элементы динамики вращательного движения твердого тела
- •Вращение твердого тела относительно неподвижной оси
- •4.2. Момент инерции
- •4.3. Примеры вычисления моментов инерции однородных симметричных тел
- •4.4. Кинетическая энергия вращающегося твердого тела
- •Механическая работа при вращательном движении твердого тела
- •4.6. Сравнение описаний движения материальной точки и вращения твердого тела
- •Применение основных законов динамики твердого тела при решении конкретных задач
- •5. Основы специальной теории относительности (сто)
- •5.1. Преобразования Галилея. Принцип относительности Галилея
- •Любая система отсчета , движущаяся относительно некоторой инерциальной системы отсчета равномерно и прямолинейно, также является инерциальной.
- •5.2. Опыт Майкельсона. Постулаты теории относительности
- •Принцип постоянства (инвариантности) скорости света
- •5.3. Преобразования Лоренца
- •5.4. Следствия из преобразований Лоренца
- •5.4.1. Лоренцовское сокращение длины
- •5.4.2. Относительность промежутков времени
- •5.4.3. Относительность одновременности
- •5.5. Релятивистский закон сложения скоростей
- •5.6. Релятивистские импульс и масса частицы
- •5.7. Релятивистская энергия
- •1. Релятивистская кинетическая энергия частицы определяется приращением ее полной энергии (5.23), (5.26).
- •2. Полная энергия системы и ее масса связаны универсальной формулой а. Эйнштейна (5.28).
- •5.8. Связь релятивистской энергии и импульса частицы
- •6. Ответы на контрольные вопросы
- •Кинематика
- •Динамика материальной точки
- •Законы сохранения в механике
- •Элементы динамики вращательного движения твердого тела
- •Основы специальной теории относительности
- •Оглавление
- •Уколов Александр Сергеевич
- •Часть 1
Законы сохранения в механике
3.1. Может, при условии, что .
3.2. Могут,
если до взаимодействия
![]() .
.
3.4.
![]() -
равнодействующая внешних сил, если
система частиц - твердое тело.
-
равнодействующая внешних сил, если
система частиц - твердое тело.
3.5.
![]() ,
где
,
где
![]() -
проекция результирующего вектора
перемещения
-
проекция результирующего вектора
перемещения
![]() на направление действия силы.
на направление действия силы.
3.6.
![]() ,
так как
,
так как
![]() .
.
A
Рис. 6.2
![]() .
С другой стороны, так как поле потенциально,
то
.
С другой стороны, так как поле потенциально,
то
![]() ,
а
,
а
![]() .
Поэтому
.
Поэтому
![]() .
В непотенциальном силовом поле работа
по замкнутому пути может быть равна
нулю, если
в любой точке этого силового поля
(пример: магнитное поле).
.
В непотенциальном силовом поле работа
по замкнутому пути может быть равна
нулю, если
в любой точке этого силового поля
(пример: магнитное поле).
3.8.
Силовое поле, изображенное на рис. 3.6,
непотенциально, так как
![]() .
Действительно, для контура 12341 имеем
.
Действительно, для контура 12341 имеем
![]() .
Здесь учтено, что (рис. 6.3)
.
Здесь учтено, что (рис. 6.3)
3
2
4
1
Рис. 6.3




![]() ,
так как
,
так как
![]() и
и
![]() .
Кроме того, для
указанного поля
.
Кроме того, для
указанного поля
![]() ,
поэтому
,
поэтому
![]() .
С учетом
.
С учетом
![]() ,
,
![]() имеем
имеем
![]() .
.
3.9.
Может, если
![]() и
и
![]() .
.
Рис. 6.4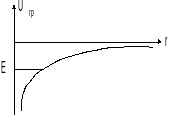
3.12. В этом случае алгебраическая сумма проекций моментов сил на данное направление должна равняться нулю.
Рис. 6.5
![]() относительно некоторой точки
.
Тогда относительно любой другой точки
относительно некоторой точки
.
Тогда относительно любой другой точки
![]() (рис. 6.5)
(рис. 6.5)
0
m
Рис. 6.6
![]()

![]()
![]()

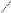


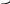

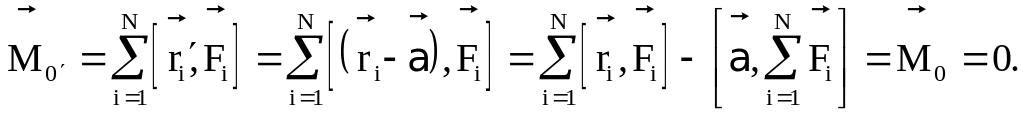
3.14.
![]()
![]()
Обозначения ясны из рис. 6.6. В ответе учтено, что
![]()
Элементы динамики вращательного движения твердого тела
4.1.
Можно. В этом случае ось вращения
является мгновенной осью, а векторы
![]() и
и
![]() определяют угловое ускорение и момент
сил относительно этой мгновенной оси.
определяют угловое ускорение и момент
сил относительно этой мгновенной оси.
4.2.
Угловое ускорение уменьшается в этом
случае обратно пропорционально радиусу
окружности. На результат большее влияние
оказывает увеличение момента инерции
точки
![]() ,
чем увеличение величины момента
касательной силы
,
чем увеличение величины момента
касательной силы
![]() .
.
4.4. При вращении твердого тела относительно оси, проходящей через неподвижный центр масс.
4.5.
![]()
Здесь
учтено, что плоское движение твердого
тела представимо в виде совокупности
поступательного и вращательного
движений, а также (1.44) и (3.5).
-
скорость поступательного движения тела
(некоторой его точки
);
-
угловая скорость вращения относительно
оси, проходящей через точку
;
![]() -
момент инерции тела относительно этой
оси;
-
момент инерции тела относительно этой
оси;
![]() -
радиус-вектор центра масс относительно
точки
.
-
радиус-вектор центра масс относительно
точки
.
4.6.
![]()
![]()
![]() Произведя циклическую перестановку
сомножителей в смешанном произведении,
получим:
Произведя циклическую перестановку
сомножителей в смешанном произведении,
получим:
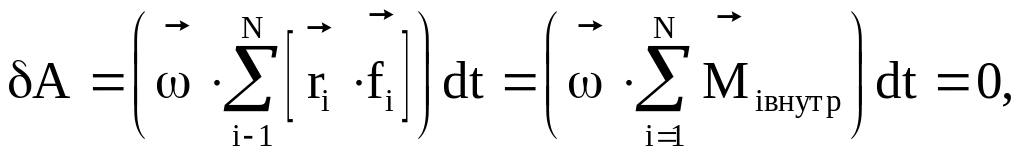
так как сумма моментов внутренних сил равна нулю (см. п. 3.9).
4.7. Смотри предыдущий ответ.
![]()

(последнее равенство справедливо в случае неподвижной оси вращения).
4.8. Да. , где - результирующий момент силы относительно некоторой неподвижной в данный момент времени точки , а - элементарный угол поворота относительно мгновенной оси, проходящей через точку .
4.9. Так как стержень вращается вокруг неподвижной оси, проходящей через точку , то его полная энергия в произвольном положении (рис. 4.6) определяется выражением
![]() где
где
![]()
Эта энергия
остается постоянной, так как поле силы
тяжести потенциально, а момент силы
![]() относительно оси вращения равен нулю,
поэтому работы не совершает. Итак,
относительно оси вращения равен нулю,
поэтому работы не совершает. Итак,
![]()
Учтя, что
![]() ,
получим для
выражение
,
получим для
выражение
![]()
4.10.
а)
-
направлен горизонтально, если
![]() .
Из (4.38) имеем
.
Из (4.38) имеем
![]()
![]() и
и
![]() .
.
б)
-
направлен вертикально, если
![]() .
Из (4.37) имеем
.
Из (4.37) имеем
![]() .
Откуда
.
Откуда
![]()
![]()
в)
-
направлен вдоль стержня, если
![]() или
или
![]() .
В обоих случаях
.
В обоих случаях
![]() ,
поэтому с учетом (4.37) и (4.38) имеем
,
поэтому с учетом (4.37) и (4.38) имеем
![]()
что выполняется только при двух положениях стержня:
и
![]()
