1.3.6. Взаимосвязь между линейными и угловыми кинематическими величинами

Из соотношения (1.27) непосредственно следует, что

или с учетом (1.5) и (1.28)

. (1.30)

Из (1.30) следует, что и , а величина скорости . При движении точки вокруг неподвижной оси (рис 1.9, а) ( , где R-радиус окружности), для модуля скорости имеем

(1.31)

Дифференцируя соотношение (1.30) по времени, получим

,

или, используя (1.14), (1.29) и (1.5),

. (1.32)

Первое слагаемое представляет собой тангенциальную составляющую ускорения:

, (1.33)

а второе слагаемое - нормальную составляющую ускорения

. (1.34)

Чтобы убедиться в справедливости (1.33) и (1.34), рассмотрим

вращение точки вокруг неподвижной оси. В этом случае

.

Здесь использованы формулы (1.26), (1.29), (1.31), (1.19) и учтено, что R=const. Для (1.34) с учетом и (1.31), (1.21) получим

Выводы: Вращательное движение материальной точки в равной мере может описываться как с помощью линейных кинематических величин , , , так и с помощью угловых , , . Между линейными и угловыми величинами существует взаимная связь, выражаемая соотношениями (1.27), (1.30) и (1.32-1.34).

1.4. Кинематическое уравнение движения. Прямая и обратная задачи кинематики

Как было указано выше в п.1.3, характер движения точки и вид ее траектории описывают кинематическими уравнениями движения , {x(t), y(t), z(t)}, которые однозначно определяют положение материальной точки в любой момент времени t относительно выбранной системы отсчета.

При решении конкретных задач кинематики могут возникать две принципиально различные ситуации в зависимости от того, какая информация известна о движении точки.

1. Прямая задача кинематики. Известен математический вид кинематического уравнения движения. Необходимо найти кинематические характеристики и . В этом случае задача однозначно решается с помощью (1.5), (1.6), (1.14), (1.15).

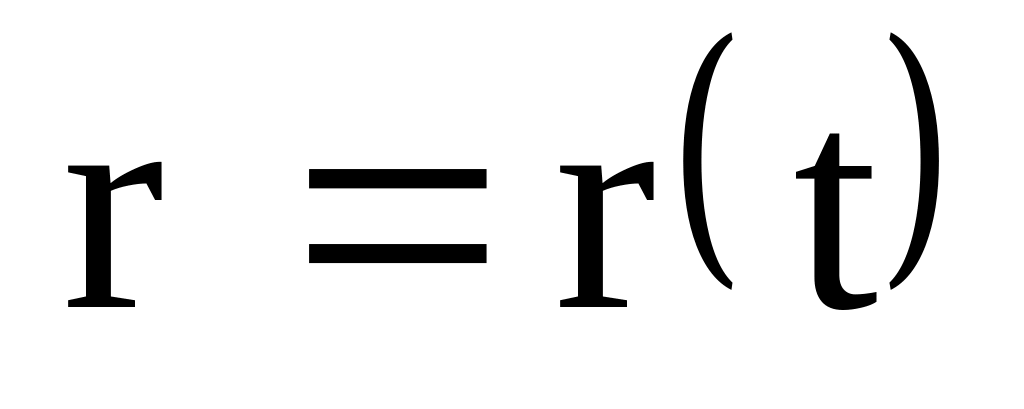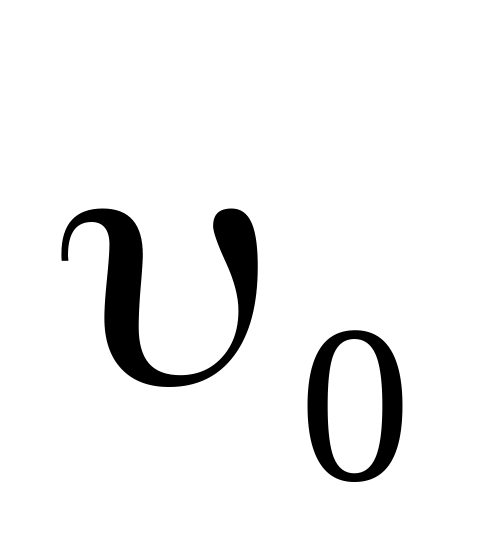2. Обратная задача кинематики. Известна одна из кинематических характеристик движения как функция времени (например, ). Необходимо определить остальные кинематические величины: и кинематическое уравнение движения . В этом случае однозначное решение задачи может быть найдено только при наличии дополнительной информации. Должны быть известны кинематические величины и 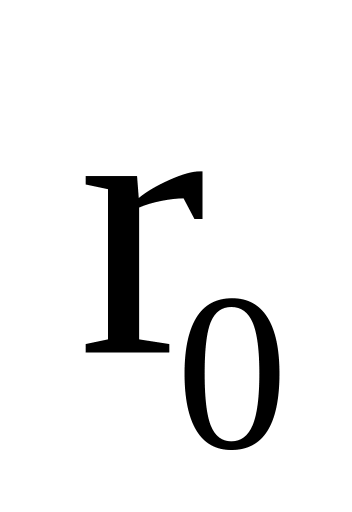в некоторый момент времени t₀, условно принятый за начальный. Величины и называются начальными условиями задачи. Тогда с помощью (1.14) будем иметь

.

Интегрируя в пределах от t₀ до t, получим

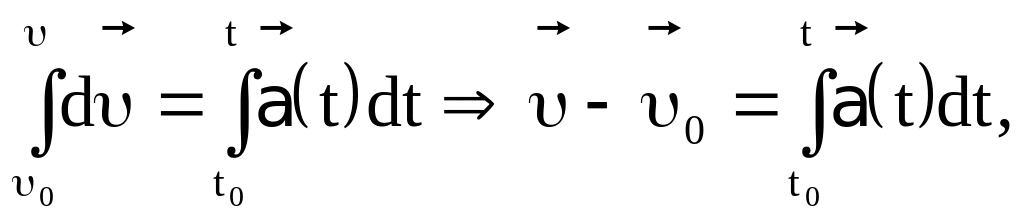
то есть

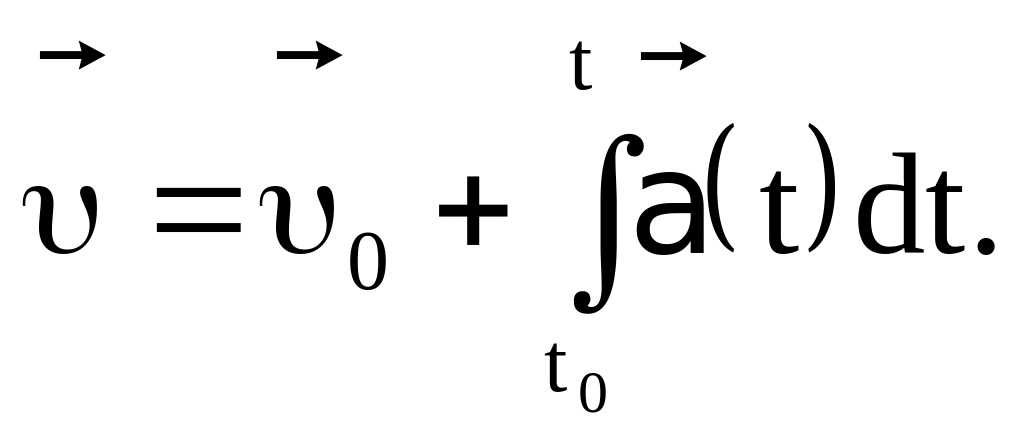(1.35)

Кинематическое уравнение движения найдем на основании (1.5) с учетом (1.35)

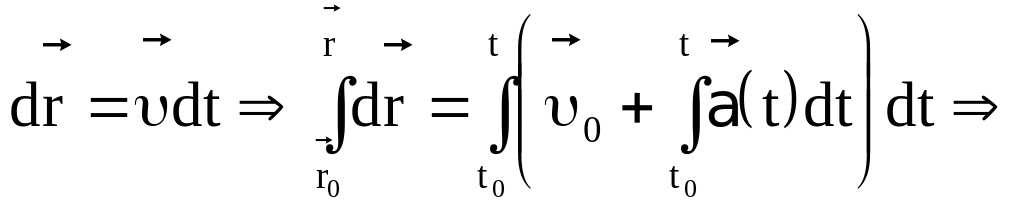
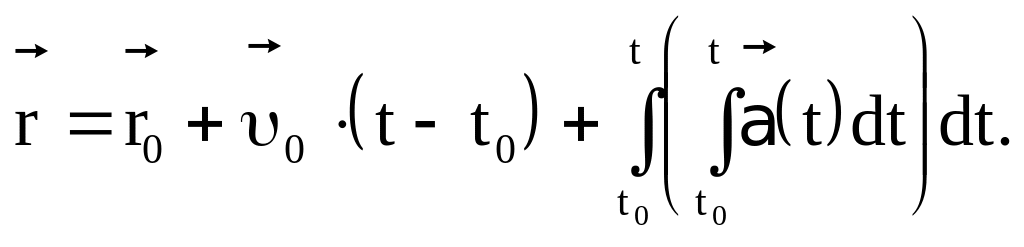(1.36)

В качестве примера рассмотрим решение обратной задачи о движении точки с постоянным ускорением . В этом случае из (1.32) имеем

, (1.37)

а из (1.36)

, (1.38)

Выводы: В кинематике встречаются два типа задач: прямая и обратная. Прямая задача имеет однозначное решение. Обратная задача для однозначности решения требует знания начальных условий.

Контрольные вопросы.

1.11. Покажите, что движение с происходит в одной плоскости, а траектория точки в этой плоскости представляет ветвь параболы.

1.12.Покажите, что вращательное движение материальной точки вокруг неподвижной оси с постоянным угловым ускорением описывается кинематическими уравнениями

где и значения и при .