6. Ответы на контрольные вопросы

1. Кинематика

1.1.

1.2. а) - движение прямолинейное, - на участке 1-2 направление движения изменяется;

б) - движение криволинейное, - направление движения не изменяется.

1.4.

1.5. Может, если движение на прямолинейном участке траектории изменяет направление. Равенство выполняется при неизменном направлении движения, когда .

1.6. а) Условие означает, что при движении (см. 1.10) может изменяться только модуль радиус-вектора. Поэтому движение прямолинейное на одной из ветвей прямой, проходящей через точку отсчета. Характер этого движения может быть любой, он определяется зависимостью модуля радиус-вектора от времени .

б) Условие , означает, что направление вектора неизменно (движение прямолинейное) и модуль скорости постоянен (движение равномерное).

в) траектория лежит на поверхности сферы.

вид траектории, вообще говоря, произволен.

г) Условие эквивалентно (см. случай а)).

д) Условие означает, что , а означает, что , следовательно, указанные условия определяют равномерное движение по окружности.

1.7. а) означает, что , а означает, что . Оба условия выполняются, если движение равномерное и прямолинейное;

б) равнопеременное прямолинейное движение;

в) прямолинейное движение, характер его определяется зависимостью ;

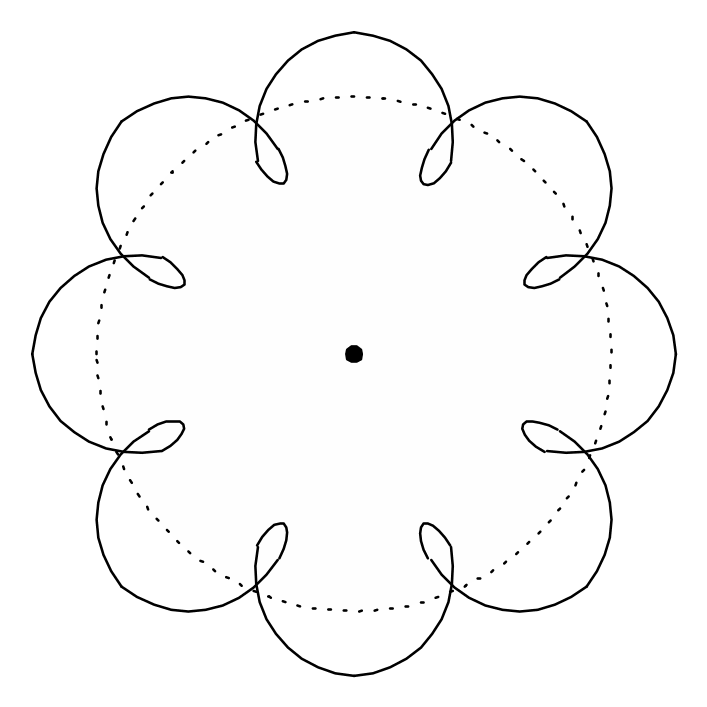
г) равномерное движение по винтовой линии.

1.8. Возможен только тривиальный случай (прямолинейное движение).

9. В этом случае 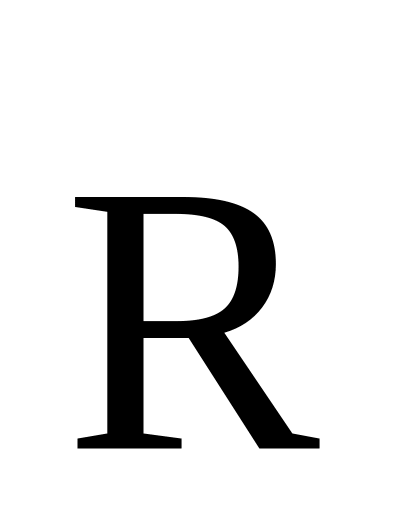является радиусом кривизны траектории относительно мгновенной оси вращения.

10. а) равномерное вращение;

б) равнопеременное вращение вокруг мгновенной оси;

в) равнопеременное вращение вокруг неподвижной оси;

г) условие означает, что , а означает, что , то есть материальная точка равномерно вращается по окружности, плоскость которой в свою очередь равномерно поворачивается относительно неподвижного диаметра.

1.11. Если выбрать систему координат так, чтобы одна из ее плоскостей (например X0Y) совпадала с плоскостью, в которой лежат постоянные векторы и , то в этом случае и , поэтому из (1.38) сразу следует , что и означает движение в плоскости, параллельной X0Y. Если при этом одну из осей (например 0X) направить вдоль , то (1.38) примет вид:

Исключая из первых двух соотношений время , получим:

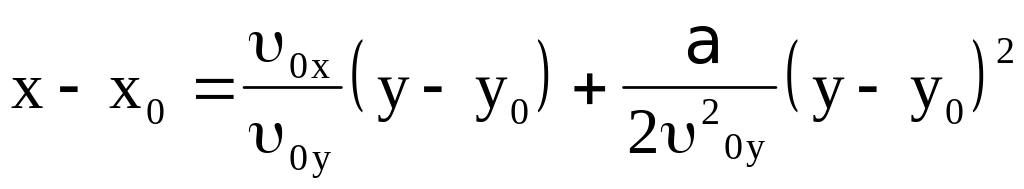- уравнение параболы, лежащей в плоскости .

1.12. Уравнения (1.39), (1.40) получаются непосредственно из (1.37) и (1.38) с учетом (1.27), (1.30) и (1.33) для модулей векторов.

1.13. а) Можно, вокруг мгновенной оси вращения.

б) Нельзя.

1.14. Может.

2. Динамика материальной точки

Рис. 6.1

2.2. Если и , то .

2.3. Из рис. 6.1. видно, что при отклонении нити на угол от вертикали ,

, а . Если при этом , то , поэтому .

В пределе при , .

4. При 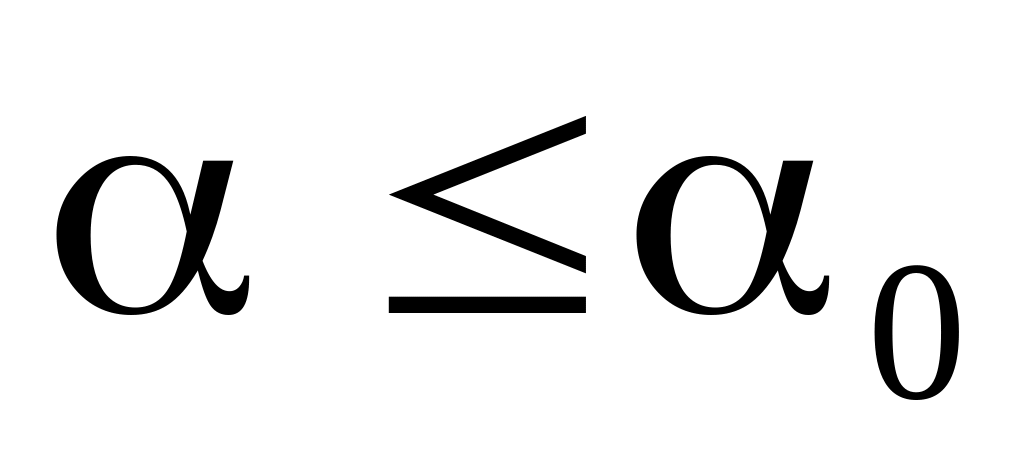(покой), .

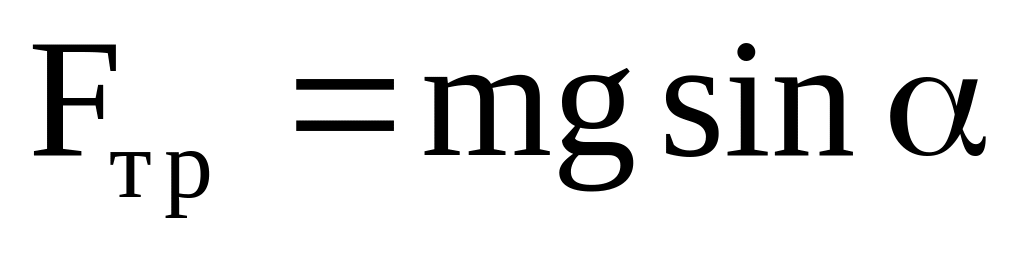При (скольжение), , причем при . Здесь - угол наклона.