5.4.3. Относительность одновременности

В механике больших скоростей существует еще один интересный эффект, связанный с относительностью понятия одновременности.

Определим вначале это понятие.

События называются одновременными, если они происходят в один и тот же момент времени, измеренный по часам этой системы координат.

Пусть в системе отсчета происходят два каких-либо события:

- первое в точке в момент ;

- второе в точке в момент .

Для этих событий в системе :

а) если эти события в системе пространственно совмещены и происходят одновременно , то, как непосредственно следует из (5.5), пространственная совмещенность и одновременность сохраняется в любой другой инерциальной системе отсчета;

б) если в системе в ее различных точках происходят два одновременных события , то в системе отсчета , движущейся относительно , эти события остаются пространственно разобщенными и становятся неодновременными . Действительно, из преобразований (5.5)

.

С учетом

следует

и

(5.16)

Последнее соотношение и доказывает тот факт, что одновременность в механике релятивистских скоростей понятие относительное.

5.5. Релятивистский закон сложения скоростей

Одним из важнейших вопросов релятивистской кинематики является установление правила преобразования скоростей при переходе от одной инерциальной системы отсчета к другой. Дело в том, что закон сложения скоростей (5.3), следующий из преобразований Галилея, предполагает существование движений со скоростями, большими скорости света в вакууме, что противоречит основным принципам СТО. Установить вид преобразования скорости в релятивистском случае несложно. Для этого продифференцируем равенства (5.5)

Первые три равенства почленно разделим на четвертое:

В правых частях последних равенств произведем почленное деление числителя и знаменателя на и с учетом

получим выражения для проекций векторов скорости и в виде

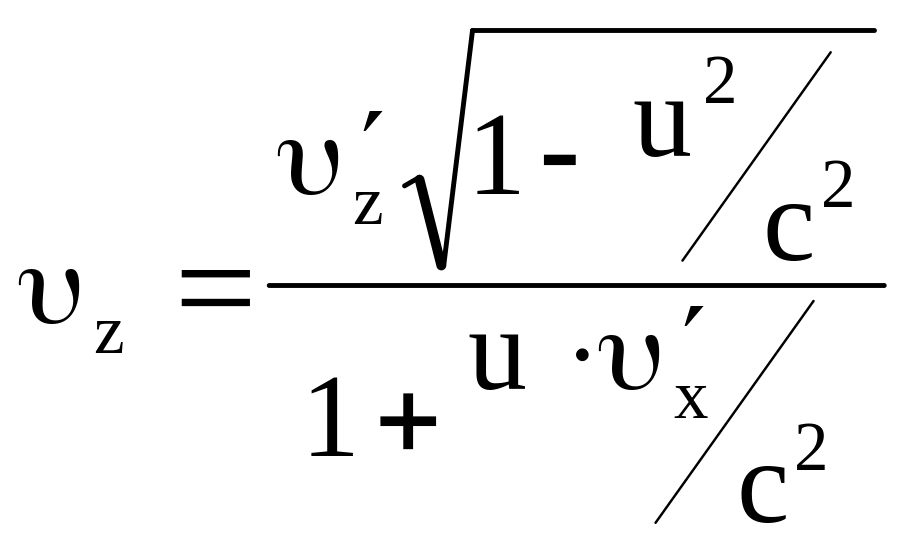. (5.17)

Выражения для проекций скоростей в системе легко получить заменой в соотношениях (5.17) на и наоборот, и на , то есть

(5.18)

Равенства (5.17) и (5.18) в теории относительности носят название релятивистского закона сложения скоростей и позволяют, зная скорость частицы в одной инерциальной системе отсчета, находить скорость этой частицы в другой инерциальной системе отсчета.

Легко видеть, что для систем отсчета и , изображенных на рис. 5.2, в случае ; формулы (5.17) переходят в классический закон сложения скоростей (5.3), записанный в проекциях на оси координат систем и :

; ; .

Контрольные вопросы.

5.7. Покажите, используя (5.17) или (5.18), что если в одной из инерциальных систем отсчета скорость частицы приближается к скорости света в вакууме , то и в любой другой инерциальной системе отсчета она стремится к .

5.6. Релятивистские импульс и масса частицы

В этом и последующих пунктах будут введены основные понятия и соотношения релятивистской динамики. Необходимость пересмотра классических представлений динамики Ньютона при переходе к динамике релятивистских скоростей вытекает из следующих соображений.

Как уже указывалось в пункте 5.1, из преобразований Галилея (5.2) следует (5.4), что непосредственно свидетельствует об инвариантности второго закона Ньютона по отношению к преобразованиям Галилея.

Нетрудно показать, что в релятивистском случае связь между ускорениями и в различных инерциальных системах отсчета более сложная. В частности, для и она имеет вид

. (5.19)

Это означает, что произведение с независящей от скорости массой не является инвариантом относительно преобразований Лоренца. Поэтому классическое определение импульса частицы для релятивистского случая требует уточнения. Можно показать, что правильное выражение для импульса частицы в релятивистском случае имеет вид

(5.20)

Наиболее строго это следует из требования инвариантности закона сохранения импульса относительно преобразований Лоренца. В случае релятивистское выражение (5.20) переходит в классическое, как и должно быть, .

Если ввести понятие релятивистской массы частицы

(5.21)

где - независящая от скорости (инвариантная) величина, называемая массой покоя, то формально сохраняется классический вид определения импульса .

Релятивистски инвариантный основной закон динамики

(5.22)

имеет ту же форму, что и классический второй закон Ньютона, но с учетом релятивистского (5.20) выражения для импульса частицы.

Отметим, что из определения релятивистской массы (5.21) непосредственно следует, что СТО допускает движение со скоростью только таких частиц, у которых масса покоя равна нулю. Более того, из (5.21) видно, что такие частицы могут существовать только в единственном состоянии, двигаясь точно со скоростью .

Контрольные вопросы.

8. Докажите справедливость (5.19).

9. Как будут изменяться компоненты скорост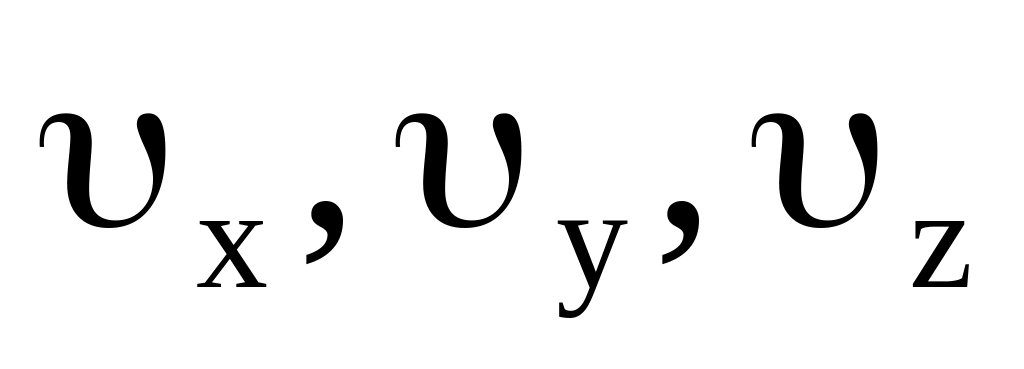и релятивистской частицы, если на нее подействует сила, направленная в ту же сторону, что и ?
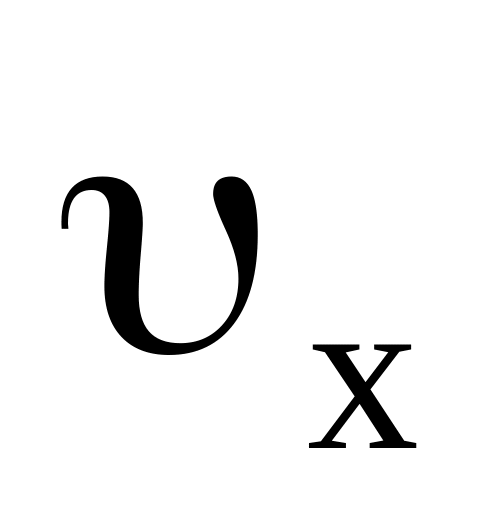