4.4. Кинетическая энергия вращающегося твердого тела
Поскольку твердое тело представляет собой частный случай системы материальных точек, то кинетическая энергия тела при вращении вокруг неподвижной оси Z будет равна сумме кинетических энергий всех его материальных точек, то есть
Все
материальные точки
твердого тела вращаются в этом случае
по окружностям с радиусами
и с одинаковыми угловыми скоростями
.
Линейная скорость каждой материальной
точки твердого тела равна
.
Кинетическая энергия твердого тела
примет вид
Сумма в
правой части этого выражения в соответствии
с (4.4) представляет собой момент инерции
этого тела
относительно данной оси вращения.
Поэтому формула для расчета кинетической
энергии вращающегося относительно
неподвижной оси твердого тела примет
окончательный вид:
.
(4.21)
Здесь
учтено, что
Вычисление кинетической энергии твердого тела в случае произвольного движения значительно усложняется. Рассмотрим плоское движение, когда траектории всех материальных точек тела лежат в параллельных плоскостях. Скорость каждой материальной точки твердого тела, согласно (1.44), представим в виде
,
где в
качестве мгновенной оси вращения выберем
ось, проходящую через центр инерции
тела перпендикулярно плоскости траектории
какой-либо точки тела. В этом случае в
последнем выражении
представляет собой скорость центра
инерции тела,
-
радиусы окружностей, по которым вращаются
точки тела с угловой скоростью
вокруг оси, проходящей через центр его
инерции. Так как при таком движении
,
то вектор, равный
,
лежит в плоскости траектории точки.
На основании сказанного выше кинетическая энергия тела при его плоском движении равна
.
Возводя выражение, стоящее в круглых скобках, в квадрат и вынося за знак суммы постоянные для всех точек тела величины, получим
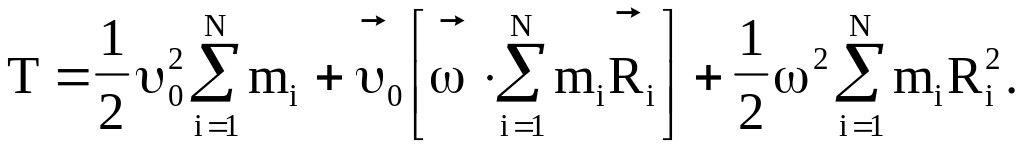(4.22)
Здесь учтено, что .
Рассмотрим
каждое слагаемое в правой части последнего
выражения отдельно. Первое слагаемое
в силу очевидного равенства
равно
.
Второе
слагаемое равно нулю, так как сумма
определяет радиус-вектор центра инерции
(3.5), который в данном случае лежит на
оси вращения. Последнее слагаемое с
учетом (4.4) примет вид
.
Теперь, окончательно, кинетическая
энергия при произвольном, но плоском
движении твердого тела может быть
представлена в виде суммы двух слагаемых:
,
(4.23)
где первое слагаемое представляет собой кинетическую энергию материальной точки с массой, равной массе тела и движущейся со скоростью, которую имеет центр масс тела;
второе слагаемое представляет собой кинетическую энергию тела, вращающегося вокруг оси (движущейся со скоростью ), проходящей через его центр инерции.
Выводы: Итак, кинетическая энергия твердого тела при его вращении вокруг неподвижной оси может быть вычислена с помощью одного из соотношений (4.21), а в случае плоского движения с помощью (4.23).
Контрольные вопросы.
4.4. В каких случаях (4.23) переходит в (4.21)?
4.5. Как будет выглядеть формула для кинетической энергии тела при его плоском движении, если мгновенная ось вращения не проходит через центр инерции? Каков при этом смысл входящих в формулу величин?
4.6. Покажите, что работа внутренних сил при вращении твердого тела равна нулю.