3.10. Момент силы. Момент импульса



m

0

Рис. 3.13

Здесь рассмотрим некоторые свойства введенных в предыдущем пункте понятий момента силы и момента импульса.

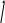
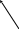
Моментом силы, действующей на частицу, относительно точки названа величина (3.48)

.

Модуль и направление вектора определяются свойствами векторного произведения двух векторов:

- модуль вектора численно равен площади параллелограмма, построенного на векторах и , как на сторонах, то есть:

(3.55)

где - расстояние от начала отсчета О до линии, вдоль которой действует сила , называется плечом силы;

- направление вектора момента силы определяется по правилу правого винта; вектор направлен перпендикулярно плоскости, в которой лежат векторы и , и совпадает с направлением поступательного движения правого винта при его вращении от к кратчайшим путем. В силу условности выбора направления вектора момент силы является псевдовектором.

Часто необходимо знать величину проекции момента силы на некоторую ось ОZ, проходящую через точку О. В этом случае эту проекцию называют моментом силы относительно данной оси:

(3.56)

z





0

Рис. 3.14

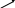
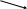
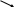
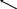
Силу можно разложить на три составляющие вдоль трех взаимоперпендикулярных направлений:

- вдоль оси ОZ - ;

- вдоль радиального R направления, перпендикулярного оси ОZ - ;

- перпендикулярно плоскости, в которой лежат ось ОZ и точка приложения силы - , то есть

= _u + + .

Определение (3.56) примет вид

.

Первое и второе слагаемые в правой части последнего равенства равны нулю, так как векторы и перпендикулярны оси ОZ, поэтому их проекции на ось ОZ равны нулю. Теперь

(3.57)

Момент импульса относительно точки определяется таким же по форме математическим выражением, что и момент силы:

(3.58)

где - -угол между векторами и ,

- - плечо импульса частицы относительно точки отсчета. Поэтому рассмотренные особенности вектора момента силы и его проекции на ось ОZ оказываются такими же и для вектора .

В частности,

(3.59)

- проекция момента импульса частицы относительно оси ОZ, проходящей через начало отсчета О.

Контрольные вопросы.

3.14. Определите величину момента импульса частицы m относительно точки, если скорость частицы постоянна и равна , а частица мимо точки О пролетает на минимальном расстоянии r_min.

4. Элементы динамики вращательного движения твердого тела

1. Вращение твердого тела относительно неподвижной оси

z

R_i

m_i

0

Рис. 4.1

Пусть твердое тело вращается вокруг некоторой оси, неподвижной относительно выбранной системы отсчета. Положение и ориентация оси остаются при вращении тела неизменными. Направим вдоль оси вращения положительное направление оси ОZ системы отсчета (рис. 4.1). В этом случае все точки твердого тела вращаются по окружностям, центры которых лежат на оси ОZ. Движение твердого тела, как системы материальных точек, описывается проекцией уравнения моментов (3.53) на ось ОZ

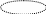
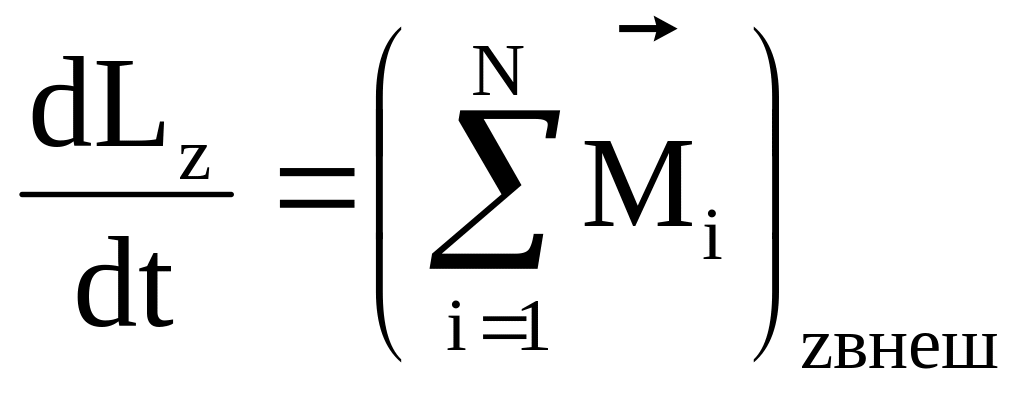(4.1)

где согласно (3.54) и (3.59)

(4.2)

Так как все точки тела при его вращении имеют одинаковые угловые скорости , то, используя (1.31): , выражение (4.2) можно записать в виде

(4.3)

Введем некоторые определения:

- для твердого тела сумму моментов внешних сил назовем результирующим моментом сил;

- сумму

(4.4)

назовем моментом инерции твердого тела относительно данной оси. Отметим, что, по определению, - момент инерции твердого тела относительно данной оси является аддитивной величиной и не зависит от времени t. С учетом введенных определений уравнение (4.1) примет вид

(4.5)

Уравнение (4.5) называется основным уравнением динамики вращательного движения твердого тела вокруг неподвижной оси. Уравнение (4.5) можно записать в другой форме, если учесть, что :

(4.6)

В частности, если проекция результирующего момента внешних сил на неподвижную ось равна нулю, то есть , то

=> ,

вращение вокруг этой оси является равномерным.

Отметим, наконец, что основное уравнение динамики вращательного движения твердого тела вокруг неподвижной оси, записанное в виде

, (4.7)

является аналогом второго закона Ньютона для прямолинейно движущейся материальной точки (сила имеет неизменное направление).

Выводы: Вращательное движение твердого тела вокруг неподвижной оси описывается основным уравнением динамики (4.5). Характер вращения определяется результирующим моментом сил относительно оси вращения, действующих на тело, и моментом инерции этого тела относительно той же оси.

Контрольные вопросы.

4.1. Можно ли основное уравнение динамики вращательного движения (4.6) или (4.7) записать в векторном виде? Если нет, то почему? Если да, то какой смысл будут иметь величины и в этом уравнении?