3.8.2. Абсолютно упругий удар двух материальных точек

Характерной особенностью абсолютно упругого удара материальных точек является сохранение их общей кинетической энергии до и после удара. Кроме этого, непосредственно до и после удара выполняется закон сохранения импульса. Пусть массы соударяющихся частиц равны m₁ и m₂, их скорости до удара и , а после удара и (рис.3.10).

m₂

m₁

0

0

x

x

а б

Рис. 3.10

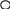
Законы сохранения, описывающие состояния точек до и после удара, в этом случае имеют вид

(3.43)

В случае центрального удара, когда до удара частицы двигались вдоль прямой, соединяющей эти частицы ( рис. 3.10), запишем систему (3.43) в проекциях на положительное направление (ОХ), выбранное вдоль этой прямой:

(3.44)

Отметим сразу особенность этой системы уравнений относительно скоростей соударяющихся частиц. Эта система однородна, поэтому всегда имеет тривиальное решение:

; .

Это решение, вообще говоря, имеет физический смысл. Оно реализуется, например, в случае, когда в промежутке между моментами времени t₁ и t₂ удара не произошло. Нас здесь не будет интересовать это решение . Для дальнейшего решения и анализа его результатов удобно ввести безразмерный параметр - относительную массу соударяющихся частиц: , тогда система (3.44) примет вид

При дальнейших преобразованиях первого уравнения учтем второе равенство системы оставим без изменения

Решение этой системы уже не представляет труда:

(3.45)

Проведем анализ полученных соотношений. Для простоты будем считать, что перед ударом частица m₂ покоилась, т.е. . Это условие всегда можно реализовать выбором соответствующей инерциальной системы отсчета, движущейся с такой же скоростью , что и вторая частица до удара.

Наиболее “впечатляющие ” результаты получаются в предельных случаях, когда массы частиц различаются очень сильно или равны между собой:

a)

При этих условиях параметром по сравнению с единицей в формулах (3.45) можно пренебречь:

и

Это означает, что “легкая” частица m₁ после удара меняет направление своего движения на противоположное, скорость этой частицы по величине “слегка” уменьшается.

“Тяжелая” частица m₂ после удара движется в направлении движения частицы m₁ до удара с “малой” скоростью u_2.

Этот случай легко понять с точки зрения здравого смысла: представьте себе шарик от пинг-понга, налетающий на массивное чугунное ядро.

б)

При этих условиях в формулах (3.45) единицей по сравнению с можно пренебречь, поэтому

Эти результаты означают, что “тяжелая” частица m₁ после удара движется в том же направлении, что и до удара, практически не изменяя величины своей скорости. “Легкая” частица m₂ после удара движется в том же направлении, что и “тяжелая” практически с удвоенной скоростью “тяжелой”.

Представьте себе массивное чугунное ядро, налетающее на шарик от пинг-понга.

в) В этом случае то есть частицы обмениваются скоростями: налетающая частица m₁ после удара останавливается, а первоначально покоящаяся частица m₂ движется со скоростью налетающей частицы.

Контрольные вопросы.

3.11. Рассмотрите самостоятельно случай абсолютно неупругого удара, когда в результате удара частицы “слипаются” и движутся после удара как единое целое.