9.3. Краевая задача: метод прогонки.

Рассмотрим метод прогонки на примере решения уравнения второго порядка вида

Y”+p(X)Y’+q(X)Y=f(X)

на отрезке [Х₀, Х_n] с заданными граничными условиями Y(Х₀)=Y₀=А и Y(Х_n)=Y_n=В. Смысл решения заключается в расчете таблицы приближенных значений искомой функции Y(Х) в узлах Х_i= Х₀+ih, где h=(Х_n - Х₀)/n и i=1,2,...,n-1.

Заменим приближенно в каждом внутреннем узле производные Y” и Y’ конечными центрально-разностными отношениями

Y_i“=( Y_i+1 -2Y_i + Y_i-1)/h² и Y_i‘=( Y_i+1 - Y_i-1)/(2h).

Обозначим p_i=p(Х_i), q_i=q(Х_i), f_i=f(Х_i).

Используя эти формулы, приближенно заменим исходное дифференциальное уравнение второго порядка на систему линейных алгебраических уравнений

( Y_i+1 -2Y_i + Y_i-1)/h² + p_i ( Y_i+1 - Y_i-1)/(2h) + q_iY_i = f_i,

где i=1,2,...,n-1 , Y₀=А и Y_n=В. Решив эту систему, получим таблицу приближенных значений искомой функции. При большом n непосредственное решение такой системы, например, методом Гаусса становится громоздким. Учитывая специфический вид полученной системы алгебраических уравнений, а именно- что матрица коэффициентов ее трехдиагональна, применим специальный метод решения, называемый методом прогонки.

Запишем систему в виде

a_i Y_i-1+b_i Y_i +c_i Y_i+1 =d_i ,

где a_i =1-hp_i /2, b_i = h²q_i -2, c_i =1+hp_i /2, d_i = h²f_i.

Введем дополнительные переменные

v_i = - c_i /( b_i + a_i v_i-1) и u_i = (d_i - a_i u_i-1)/(b_i + a_i v_i-1).

Чтобы сделать схему вычислений однородной, положим a₀=0 и c_n=0. Тогда v_n=0 и Y_n=u_n. Кроме того, v₀ = - c₀/b₀ и u₀ = d₀/b₀.

Тогда решение системы определяется формулой

Y_i = u_i + v_i Y_i+1 .

Пример 9.3.

Решим задачу примера 9.1 с граничными условиями Y(1)=0,77 и Y(1,5)=0,49281, выбрав шаг 0,1 с погрешностью 0,001.

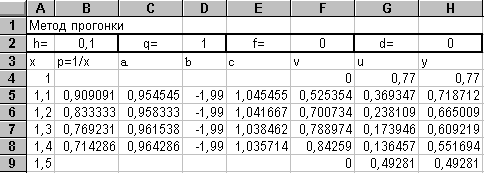
Как видно из условий задачи, h = 0,1, q=1, f=0, d=0, p=1/X для всех Х.

Откроем новый рабочий лист и выделим блок А4:А9 под значения Х от 1 до 1,5. В блок В5:В8 занесем значения 1/X, отведем столбцы С,D,E для текущих значений a_i, b_i, c_i, столбцы F и G - для значений v_i и u_i , а столбец Н - для значений Y.

Занесем числа: в ячейку F4 - ноль, в ячейки G4 и H4 - число 0,77. Соответственно, в ячейку F9 - тоже ноль, в ячейки G9 и H9 - число 0,49281.

Формулы ячеек в строке 5 представлены в таблице.

ячейка	формула
B5	=1/A5
C5	=1-B5*$B$2/2
D5	=$B$2^2-2
E5	=1+B5*$B$2/2
F5	=-E5/(D5+C5*F4)
G5	=-C5*G4/(D5+C5*F4)
H5	=G5+F5*H6

Формулы в строках 6,7,8 должны быть скопированы из строки 5. Результаты вычислений приведены ниже. Можно сравнить их с результатами расчетов в примере 10.2, чтобы оценить полученную погрешность.

10. Численное решение уравнений с частными производными

Метод сеток или метод конечных разностей является одним из самых распространенных в настоящее время методов численного решения уравнений с частными производными. В его основе лежит идея замены производных конечно-разностными отношениями. Мы ограничимся случаем двух независимых переменных.

Рассмотрим в качестве примера смешанную задачу для уравнения теплопроводности: найти значения функции U(X,T) , удовлетворяющие уравнению

dU/dT = Dd²U/dX²

с начальными условиями (т.е. при Т=0) U(X,0) = f(X) и

краевыми условиями первого рода U(0,T) = g₁(T) и U(L,T) = g₂(T).

Таким образом может быть описана задача о распространении тепла в однородном стержне длины L , на концах которого поддерживается заданный температурный режим. Соответствующей заменой переменных эту задачу можно свести к каноническому уравнению при D=1 и L=1

dU/dT = d²U/dX²

Заметим, что начальные и граничные условия должны быть согласованы, т.е. U(0,0) = f(0)= g₁(0) и U(1,0)=f(1)= g₂(0).

Построим на плоскости X0T равномерную прямоугольную сетку с шагом h в направлении Х и шагом l - в направлении Т:

Х= ih ( i= 0,1,2,...,n) и T=jk (j=0,1,2,...).

Обозначим Xi= ih и Tj= jk, а также U(Xi, Tj)=Ui,j. Любой узел этой сетки, номер которого (i,j), определяется координатами(Xi,Tj). Узлы сетки, лежащие на границе полуполосы Т>=0 и 0<=X<=1, называются граничными, все остальные узлы - внутренними. Начальные и краевые условия считаются заданными в граничных узлах сетки. Приближенно заменим в каждом внутреннем узле вторую частную производную по пространственной координате Х конечно-разностным отношением

(d²U/dX²)_i,j =( U_i,j-1 -2U_i,j + U_i,j+1)/h²,

а первую частную производную по временной координате - конечно-разностным отношением

(dU/dT)_i,j =( U_i,j+1 - U_i,j)/k.

Тогда вместо исходного дифференциального уравнения, получаем алгебраическое уравнение вида

( U_i,j+1 - U_i,j)/k = ( U_i-1,j -2U_i,j + U_i+1,j)/h².

Обозначив q=k/h² , приведем это уравнение к виду

U_i,j+1 =(1-2q)U_i,j + q(U_i-1,j+U_i+1,j).

Задавая i=0,1,2,..,n и j=0, увидим, что все слагаемые в правой части этого уравнения могут быть вычислены из граничных условий. Поэтому таким образом можно вычислить все значения U на первом временном слое при j=1. Далее, задавая j=1, можно вычислить по этой формуле значения функции U во всех узлах второго временного слоя при j=2 и т.д. Такая схема вычислений называется явной. Доказано, что вычисления по этой схеме будут устойчивы, если 0<q<= 0,5. Задавая q=0,5, получим алгебраическое уравнение

U_i,j+1 =(U_i-1,j+U_i+1,j)/2.

Таким образом, используя это уравнение, можно вычислить значения функции U на каждом временном слое через значения на предыдущем слое.

Пример 10.1.

Hайти значения функции U(X,T) , удовлетворяющие уравнению

dU/dT = Dd²U/dX²

с начальными условиями (т.е. при Т=0) U(X,0) = Sin(X) и 0<X<=1,

краевыми условиями первого рода U(0,T) = 0 и U(1,T) = 0.

Выберем по аргументу Х шаг h=0,1, т.е. n=10. Так как q=0,5, то по аргументу Т получаем шаг k=h²/2=0,005.

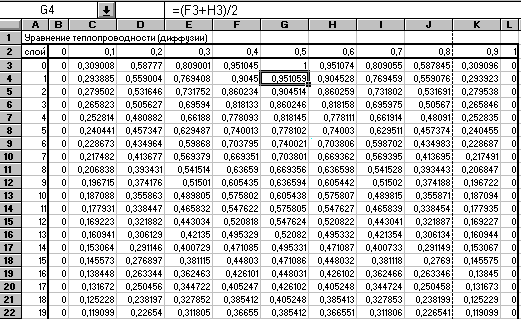
Откроем новый рабочий лист EXCEL. Отведем столбец А под номера временных слоев от 0 до, например, 25. Заполним блок А3:А28 числами от 0 до 25. Во второй строке в ячейки В2:L2 занесем значения пространственной координаты Х от 0 до 1. В блок В3:В28 и в блок L3:L28 занесем нули - значения краевых условий. В ячейку С3 занесем формулу =SIN(3,1415*C2) и скопируем ее в блок D3:K3. Тем самым введем в нулевой временной слой начальные условия. Далее в ячейку С4 введем основную расчетную формулу, полученную из алгебраического конечно-разностного уравнения =(B3+D3)/2. Эту формулу надо скопировать в блок С4:L28.

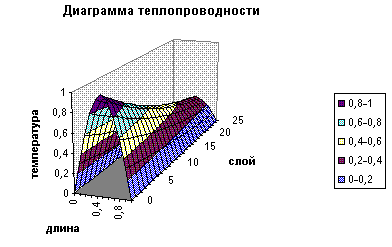
Результаты вычислений представлены в таблице для первых 19 слоев.

Как видно, таблица малообозрима, а при увеличении количества временных слоев вообще становится неудобочитаемой. Результаты расчетов лучше всего представить в виде диаграммы. Для построения диаграммы надо выделить блок А2:L28 и вызвать Мастер Диаграмм. Появится диалог из пяти шагов. На шаге 1 из 5 следует убедиться в том, что выделен блок А2:L28 и щелкнуть по кнопке Шаг>. На шаге 2 из 5 нужно выбрать тип диаграммы - Поверхность. На шаге 3 из 5 выберем формат 1 диаграммы. Далее на шаге 4 из 5 выберем Ряды данных - в строках и в полях Отвести 0 строк введем 1 так, чтобы получилось Отвести 1 строк для меток оси Х. То же самое проделаем для оси Y - Отвести 1 столбцов для меток оси Y. На последнем шаге 5 из 5 в поле Название диаграммы введем текст “Уравнение теплопроводности”, в поле Название по оси категорий(Х) введем текст - “длина”, в поле Значений (Z)- текст”температура”, в поле Рядов (Y) - текст “слой”. Щелкнув по кнопке Закончить, получим диаграмму, примерный вид которой приведен ниже.

Бурляев Валерий Викторович

Под редакцией Корнюшко В.Ф.

Численные методы в примерах на EXCEL.

Методическое пособие по дисциплине “Программирование и численные методы”.

Рецензент - д.т.н. профессор Бахвалов Л.А.

Подписано в печать

Печать офсетн., бум. офсетн., формат 60х90/16, тираж 100 экз., заказ

117571, Москва, пр. Вернадского, 86

издательско-полиграфический центр МИТХТ