
Введение
Объективная оценка нагрева кабелей необходима с точки зрения экономии кабельных материалов, поскольку результаты тепловых расчетов влияют на выбор сечения и числа кабелей в сети. Для тепловых расчетов кабелей широко применяется упрощенная математическая модель с применением тепловой схемы замещения. При этом тепловые сопротивления вычисляются по эмпирическим и полуэмпирическим формулам, которые применимы для решения ограниченного круга задач. Для ряда конструкций кабелей и условий их эксплуатации воспользоваться выше указанной методикой нельзя. Численные методы позволяют наиболее полно учесть конструктивные особенности и условия эксплуатации кабелей.
В данном руководстве предлагается исследовать стационарные и переходные тепловые режимы кабелей с помощью метода конечных элементов /МКЭ/. Благодаря своей универсальности этот численный метод в последние годы широко используется в различных областях техники. В предложенных лабораторных работах математическое моделирование теплового состояния кабелей проводится на ЕС ЭВМ.
Основные понятия
Особенности теплового расчета с помощью МКЭ рассмотрим на примере переходного теплового режима трехжильного кабеля с круглыми жилам при прокладке в воздухе /рис. 1/. Считаем, что тепловой контакт между составными частями кабеля идеальный. Материалы составных частей кабеля однородны и изотропны и имеют независимые, от температуры теплофизические характеристики. Тепловой поток в кабеле предлагается радиальным, а поле температур - двумерным, поскольку поперечные размеры кабеля намного меньше размера кабеля в осевом направлении.
Нестационарное тепловое состояние кабеля возникает при следующих условиях. В начальный момент времени поле температур в кабеле определяется известной функцией. В последующие моменты времени в жилах кабеля начинают протекать токи и появляются диэлектрические потери в изоляции и оболочке. Требуется найти распределение температур в кабеле.
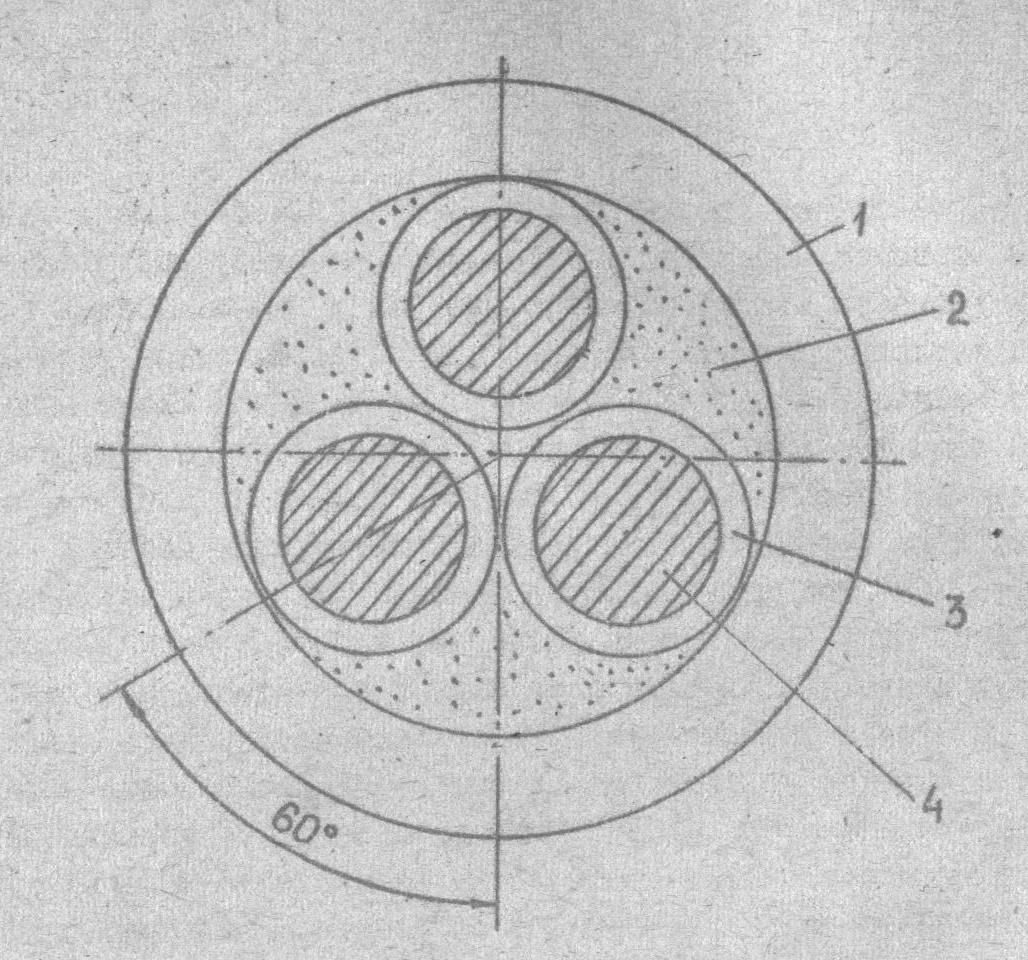
Рис I. Сечение трехжильного кабеля:
1-оболочка, 2-заполнение, 3-жильная изоляция, 4-жила
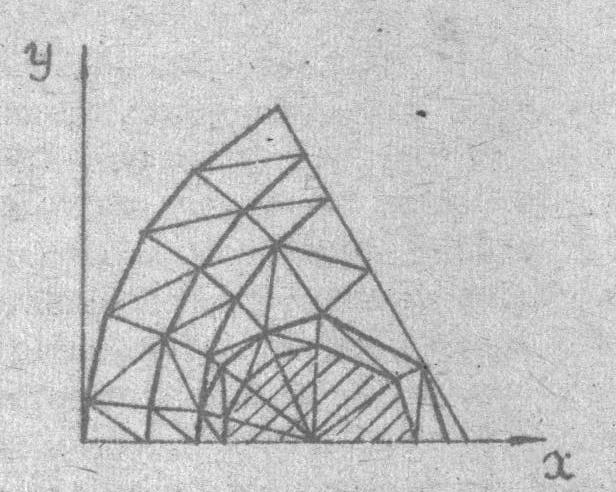
Рис 2. Разбивка части сечения кабеля
на элементы
Поставленная задача сводится к решению уравнения теплопроводности для функции температур Т в каждой области Gn, являющейся частью сечения кабеля
![]() ,
(1)
,
(1)
Где x, у - декартовы координаты;
![]() ,
,
![]() ,
,
![]() -
соответственно коэффициент теплопроводности,
удельная теплоемкость и плотность
кабельных материалов;
-
соответственно коэффициент теплопроводности,
удельная теплоемкость и плотность
кабельных материалов;
n - номер области составной части кабеля;
![]() - время;
- время;
![]() - мощность внутренних
источников теплоты, связанная с потерями
в жилах или обусловленная диэлектрическими
потерями в изоляции и потерями в оболочке.
- мощность внутренних
источников теплоты, связанная с потерями
в жилах или обусловленная диэлектрическими
потерями в изоляции и потерями в оболочке.
Предполагаем,
что величина
![]() постоянна
в пределах каждой области. На поверхностях
контакта рассматриваемых областей Gn
заданы
граничные условия сопряжения /условия
идеального контакта/. Через внешнюю
поверхность кабеля осуществляется
теплообмен с окружающим воз пухом по
закону Ньютона
постоянна
в пределах каждой области. На поверхностях
контакта рассматриваемых областей Gn
заданы
граничные условия сопряжения /условия
идеального контакта/. Через внешнюю
поверхность кабеля осуществляется
теплообмен с окружающим воз пухом по
закону Ньютона
![]() ,
(2)
,
(2)
где
![]() коэффициент теплоотдачи с наружной
поверхности кабеля;
коэффициент теплоотдачи с наружной
поверхности кабеля;
Tв - температура окружающего воздуха.
Считаем,
что
![]() не зависит от температуры.
не зависит от температуры.
Идя решения поставленной задачи в соответствии с МКЭ каждую из областей Gn разобьем на конечные элементы треугольной формы /рис. 2/. Вблизи жил, где температурный градиент наибольший, используем более мелкие элементы.
Решение совокупности уравнений теплопроводности /1/ при заданных условиях однозначности эквивалентно отысканию минимума функционала
 ,
(3)
,
(3)
Где m - число составных частей сечения кабеля.
Выразив функционал /3/ через узловые температуры и проведя его минимизацию, получаем систему линейных дифференциальных уравнений для функции температур в узлах:
![]() ,
(4)
,
(4)
где [С] - матрица демпфирования /теплоемкости/ системы, зависящая от удельных теплоемкостей и плотностей материалов;
{F}, [K]- матрица теплопроводности и вектор нагрузки;
{Т} - вектор узловых температур. Используя метод конечных разностей, получаем систему алгебраических уравнений относительно температур в узлах
![]() ,
(5)
,
(5)
где {T}0, {T}ср - узловые значения температур в начале и середине временного интервала Δτ;
{F}ср - вектор нагрузки в середине временного интервала. Считая {Т}о известными, из системы /5/ можно найти узловые температуры {Т}ср в середине временного интервала. Эта задача решается с помощью ЭВМ.
Таким образом, по известному графику изменения во времени токовой нагрузки жил и заданным диэлектрическим потерям в изоляции определяется температура жил. В результате сравнения расчетной температуры жил с ее нормативной величиной делается вывод о допустимости рассматриваемого режима работы кабеля.
При прокладке кабелей в земле необходимо учитывать ее влияние на температурное поле кабелей. Форма и размеры рассматриваемой области земли вокруг кабелей показаны на рис.3. Для окружающей кабель земли необходимо учитывать следующие граничные условия: на поверхности земли - граничное условие третьего рода /2/, на поверхности контакта кабеля и земли - условия сопряжения, а на остальной части границ области
![]()
Порядок теплового расчета такой же, как и при прокладке кабелей в воздухе. Если кабель находится в стационарном тепловом состоянии, необходимо решать уравнения вида /1/ с нулевой правой частью. Применение МКЭ в этом случав приводит к системе алгебраических уравнений относительно узловых температур.
[K]{T}+{F}=0,
которая решается с помощью ЭВМ.
МЕТОДИКА ТЕПЛОВОГО РАСЧЕТА КАБЕЛЕЙ
При выполнении тепловых расчетов кабелей встречаются два типа задач. К первому типу задач относится определение нагрузочной способности кабелей в стационарном тепловом режиме при одинаковой токовой нагрузке сил. В этом случае известна температура нагрева жил, а в результате расчета определяется допустимая токовая нагрузка. Задачи второго типа решаются при переходных тепловых режимах кабелей или в случае неодинакового тепловыделения в килах кабелей при стационарном режиме. В результате теплового расчета определяется температура жил, которая сравнивается о допустимой температурой. Методика позволяет решать оба типа задач.
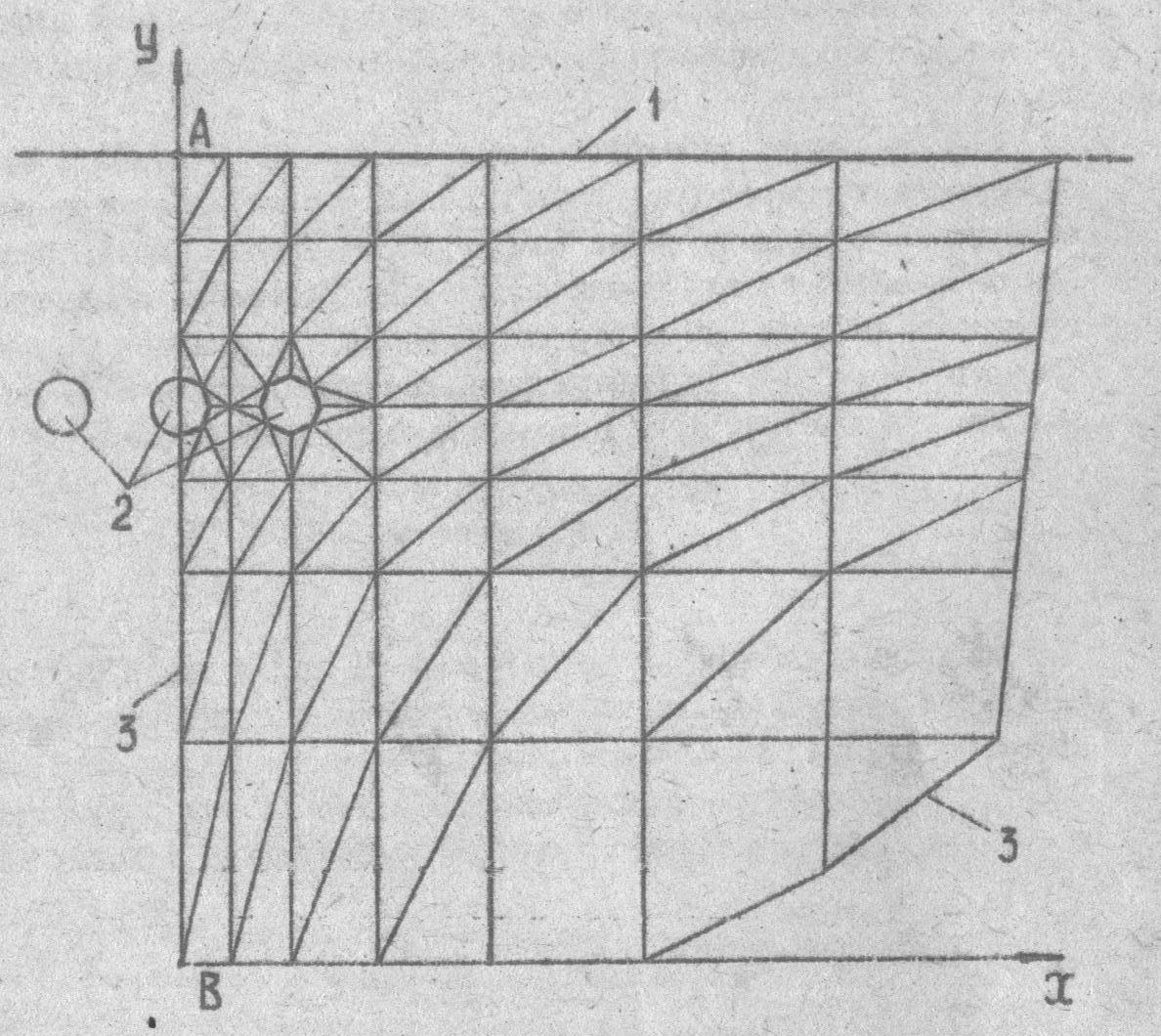
Рис.3 Область земли вокруг кабелей:
1 – поверхность земли;
2 – наружная поверхность кабелей;
3 – остальная граница рассматриваемой области земли
Тепловой расчет проводятся в следующем порядке:
1. Графическое изображение в масштабе сечения кабеля ж кабельных конструкций /труб, блоков/. При прокладке кабелей в земле изображается также область земли вокруг кабелей, ограниченная размерами: 3м в глубину, а по горизонтали - расстоянием 3м по обе стороны от кабелей. В случае симметрии теплового поля рассматривается лишь характерная часть сечения кабеля и окружающей земли.
2. Разбивка области сечения кабеля, кабельных конструкций и окружающей земли /при прокладке в земле/ на треугольные элементы. Каждая из составных частей кабеля разбивается на целое число треугольных элементов. Более мелкие элементы используются вблизи жил, где температурный градиент наибольший. Нумерация элементов производится поочередно для каждой составной части рассматриваемой области. Нумерация узлов осуществляется в направления наименьшего размера области.
3. Выбор прямоугольной систем координат и определение координат узлов.
4. В программу вводятся следующие исходные данные:
а) общее число элементов области NE ; число узлов NP номера отдельных элементов NEL и соответствующие им номера узлов /обход узлов против часовой стрелки/ и их координаты Х/1/, Х/2/, Х/3/, Y/1/, Y/2/, Y/3/; ширина полосы матрицы системы N В V , определяемая по формуле
NBW = D+1,
где D - максимальная по элементам величина наибольшей разности между номерами узлов в отдельном элементе; указатель характеристик материала /каким номерам элементов соответствуют заданные свойства материала/.
б) теплофизические характеристики - коэффициенты теплопроводности составных элементов кабеля и окружающей среды
KX1, КХ2, ...; коэффициенты теплоотдачи Н с наружной поверхности кабелей и с поверхности земли, температуры окружающего воздуха TINF1 и воздуха в трубе TINF2 /при прокладке в трубе/; номера сторон элементов, с которых имеют место теплоотдачи ISIDE /граничное условие 3-го рода/.
в) граничные условия на поверхности контакта жил и изоляции.
В случае стационарного теплового состояния при одинаковом тепловыделении в жилах на этой границе задается известная допустимая температура.
В случае переходного теплового режима или стационарного режима ghb неодинаковом тепловыделении в жилах на границе контакта ил и изоляции выполнится граничные условия вида
![]() ;
;
Tж = Tиз,
где
![]() - поверхностная плотность теплового
потока, вызванная тепловыделением в
жиле;
- поверхностная плотность теплового
потока, вызванная тепловыделением в
жиле;
I - токовая нагрузка;
ρ - удельное электрическое сопротивление;
F, L - площадь сечения и периметр жилы. При этом для каждого узла на указанной границе задается узловое значение плотности теплового потока, которое определяется как сумма величин ρζ/2 двух смежных сторон, принадлежащих границе контакта. Здесь ζ - длина стороны элемента.
г) для переходного теплового режима дополнительно вводятся: начальные температуры узлов области Т; удельные теплоемкости TEPL1, TEPL2, ...; удельные плотности R01, R02, ...; шаг по времени DT; общее число интервалов времени /критерий/; постоянная NJ, определяющая через сколько итераций печатать ;результаты расчета.
5.Определение узловых температур с помощью ЭВМ.
