4.2. Метод золотого сечения.
Как известно, золотым сечением отрезка называют деление отрезка так, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к меньшей части отрезка. Нетрудно проверить, что золотое сечение отрезка [a,b] производят две симметричные точки
Х1 = a + L(b-a) и X2 = b - L(b-a), где L = (3 - /2.
Заметим, что точка Х1 в свою очередь производит золотое сечение отрезка [a, X2], а точка X2 - золотое сечение отрезка [Х1,b].
Опишем алгоритм поиска. Начальный отрезок [a,b] делим точками Х1 и X2 по правилу золотого сечения. Вычисляем значения функций f(Х1) и f(X2). Сравнение этих значений позволяет отбросить либо интервал [a,Х1], либо интервал [X2,b]. На оставшемся интервале уже есть одна точка, производящая его золотое сечение. Поэтому следует вычислить значение второй такой точки. На этом заканчивается первая итерация. Таким образом на каждой итерации, начиная со второй, требуется лишь одно вычисление функции и при этом интервал неопределенности уменьшается на величину L ~ 0,382. Итерации продолжаются до тех пор, пока интервал неопределенности [a,b] не станет меньше заданной точности решения Е.
Пример 4.2.
Решим задачу примера 4.1 методом золотого сечения на том же рабочем листе, на котором приведено решение методом дихотомии. Величину L вычислим в ячейке Е39, а под решение отведем блок А41: G60. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 41 и 42. Формулы для остальных строк блока копируются из 42 строки. Для вычисления квадратного корня из 5 используется функция КОРЕНЬ Мастера Функций. В формулах строк 41 и 42 использован абсолютный адрес ячейки Е39, т.к. он не должен меняться при копировании.
-
Адрес
Формула
E39
(3-КОРЕНЬ(5))/2
A41
0
B41
1
C41
=A41+(B41-A41)*$E$39
D41
=B41-(B41-A41)*$E$39
E41
=2*C41^2+EXP(-C41)
F41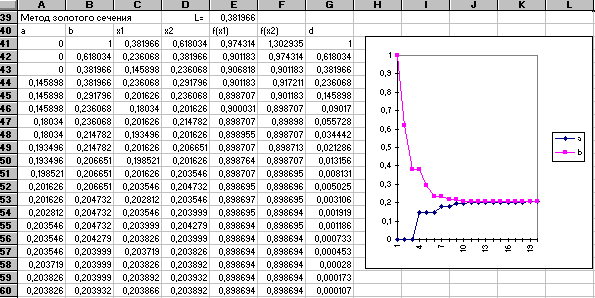
=2*D41^2+EXP(-D41)
G41
=B41-A41
A42
=ЕСЛИ(E41>F41; C41; A41)
B42
=ЕСЛИ(E41<F41; D41; B41)
C42
=ЕСЛИ(E41>F41; D41; A42+(B42-A42)*$E$39
D42
=ЕСЛИ(E41<F41; C41; B42-(B42-A42)*$E$39)
E42
=2*C42^2+EXP(-C42)
F42
=2*D42^2+EXP(-D42)
G42
=B41-A41
Как видно из таблицы, и в этом случае широко используется функция ЕСЛИ Мастера функций. После того как блок будет заполнен формулами , EXCEL предоставит решение задачи. Данный метод сходится медленнее метода дихотомии и количество итераций для получения решения с одинаковой точностью методом золотого сечения будет большей. Как и в предыдущем примере, можно построить диаграмму изменения концов интервала неопределенности.