5.2. Безусловная оптимизация: метод наискорейшего спуска.

Это метод градиентного поиска, в котором используются как значения целевой функции, так и значения ее первых частных производных. Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:

а) формулу целевой функции f(X₁,X₂, ... , Xn),

б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,

в) начальные приближения X₁₀,X₂₀ ... , Xn₀,

г) формулы первых частных производных целевой функции по каждой независимой переменной.

С помощью рассмотренного ранее метода покоординатного спуска осуществляется поиск в направлении, параллельном одной из осей координат, до точки минимума в этом направлении. Кажется разумным попытаться модифицировать этот метод таким образом, чтобы на каждом шаге поиск минимума производился вдоль “наилучшего” направления. Не ясно, какое направление является наилучшим, но известно, что направление градиента является направлением наискорейшего возрастания функции. Следовательно, противоположное направление - антиградиента - является направлением наискорейшего убывания функции.

Множество точек, для которых целевая функция имеет постоянное значение, называется линией уровня. Направление градиента перпендикулярно к любой точке линии уровня. Под градиентом понимается вектор-столбец из первых частных производных целевой функции, если она непрерывна и дифференцируема.

Идея метода наискорейшего спуска состоит в следующем. Выбираем начальную точку и вычисляем в ней градиент целевой функции. Определяем направление поиска, противоположное градиенту. Решая задачу одномерной оптимизации, ищем точку минимума целевой функции по этому направлению.

Например, для функции двух переменных формулы первой итерации будут иметь вид

u = f(X_1нов,X_2нов)  min,

где X_1нов = X₁₀- h(du/dX₁)_X10 и X_2нов = X₂₀ -h(du/dX₂) _X20, а h - длина отрезка от точки нулевого приближения до точки минимума по выбранному направлению. Эта длина определяется методом одномерной оптимизации. На этом кончается первая итерация.

В найденной точке (X_1нов,X_2нов) снова вычисляем градиент, снова определяем направление поиска, снова методом одномерной оптимизации ищем точку минимума. Эти итерации продолжаются до тех пор, пока не выполнится условие прекращения вычислений, а именно: квадратный корень из суммы квадратов частных производных целевой функции должен быть меньше заданной точности Е.

Пример 5.2.

Решим задачу примера 5.1 методом наискорейшего спуска. Для этого прежде всего найдем частные производные целевой функции

u = (X₂-X₁²)² + (1-X₁)²,

du/dX₁ = - 4(X₂-X₁²) X₁-2(1-X₁),

du/dX₂ = 2(X₂-X₁²).

Составляющие антиградиента должны быть взяты с обратным знаком

antigrad u = {- du/dX₁, -du/d X₂ }.

Будем решать задачу на том же рабочем листе, где мы исследовали метод покоординатного спуска. Выделим столбец А под переменную h, столбцы В и С - под X₁,X₂, столбцы D и Е - под составляющие антиградиента, столбцы F и G - под X_1нов,X_2нов , столбец Н - под целевую функцию u, столбец I - под переменную D. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 21 и 22. Заметим, что числовые значения в столбце А появляются в результате выполнения подпрограммы EXCEL Поиск решения для решения задачи одномерной оптимизации. Формулы блока В23:I28 получаются путем копирования в них формул блока В22:I22.

ячейка	формула
B21	0,5
C21	0,5
D21	=4*(C21-B21^2)*B21+2*(1-B21)
E21	=-2*(C21-B21^2)
F21	=B21+A21*D21
G21	=C21+A21*E21
H21	=(G21-F21^2)^2+(1-F21)^2
I21	=КОРЕНЬ(D21^2+E21^2)
B22	=F21
C22	=G21
D22	=4*(C22-B22^2)*B22+2*(1-B22)
E22	=-2*(C22-B22^2)
F22	=B22+A22*D22
G22	=C22+A22*E22
H22	=(G22-F22^2)^2+(1-F22)^2

После подготовки формул в блоке А21:I28, проведем первую итерацию. Для этого сделаем текущей ячейку Н21. Дадим команду меню Сервис- Поиск решения. В появившемся диалоге занесем в поле Установить целевую ячейку адрес Н21, а в поле Изменяя ячейки - адрес А21. Щелкнув по кнопке Выполнить, получим новый диалог, в котором щелкнем по кнопке ОК. В результате в ячейке А21 получим значение h, а ячейках F21 и В22 - новое значение Х1, в ячейках G21 и С22 - новое значение Х2.

Теперь можно приступить ко второй итерации, сделав текущей ячейку Н22. Снова используя подпрограмму Поиск решения так же, как и в первой итерации, получим очередные новые значения шага и независимых переменных. Продолжая итерации, как видно из таблицы, можно получить решение с заданной точностью за семь итераций. Точность решения контролируется по столбцу I.

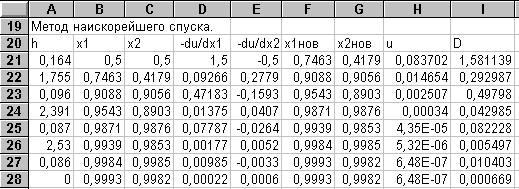
Выделяя блок В20:С28, можно построить диаграмму, аналогично примеру 5.1. На ней изображены перпендикулярные ломаные линии, причем в отличие от примера 5.1 их направление не совпадает с направлениями координатных осей.