4.3. Встроенная подпрограмма excel “Поиск решения”.
EXCEL имеет специальную подпрограмму, позволяющую решать многие оптимизационные задачи, в том числе и задачи одномерной оптимизации. Продемонстрируем применение этой подпрограммы для решения задачи из примера 4.1. Будем искать решение на том же рабочем листе. Выделим ячейку А63 для значений независимой переменной Х, а ячейку В63 - для значений целевой функции f(X). Занесем в ячейку В63 формулу =2*А63^2 + EXP(-A63).
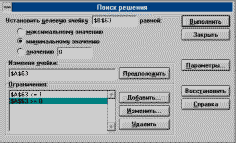
Поиск решения начинается щелчком на кнопке Выполнить. Когда программа находит решение, открывается новый диалог Результаты поиска решений. Щелчком на кнопке ОК можно сохранить найденное решение.
5. Многомерные задачи оптимизации.
В этом разделе будут рассмотрены методы, позволяющие находить минимум целевой функции многих переменных u = f(X1,X2, ... , Xn). Из курса математического анализа известно, что значения независимых переменных, при которых целевая функция достигает минимума, можно найти, решая систему нелинейных уравнений
du/dX1 = 0,
du/dX2 = 0,
....................
du/dXn = 0.
Рассмотренный прием можно использовать лишь для дифференцируемой целевой функции, но и в этом случае могут возникнуть серьезные вычислительные трудности (см. раздел 3).
Здесь мы рассмотрим численные методы оптимизации, основанные на идее целенаправленного поиска минимума. Эти методы различаются прежде всего по характеру изменения целевой функции: если нет никаких ограничений ни на изменение независимых переменных, ни на значения целевой функции, то это - методы безусловной оптимизации. При наличии каких-либо ограничений используются методы условной оптимизации.
Кроме того, методы многомерной оптимизации классифицируются по возможности использования частных производных от целевой функции: если производные не используются, то это - методы прямого поиска, в противном случае - градиентные методы.
5.1. Безусловная оптимизация: метод покоординатного спуска.
Это метод прямого поиска, в котором используются только значения целевой функции. Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:
а) формулу целевой функции f(X1,X2, ... , Xn),
б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,
в) начальные приближения X10,X20 ... , Xn0.
Зафиксируем все значения Х-ов в виде начальных приближений, кроме первого. Тогда f(X1, X20 ... , Xn0) - функция одной переменной X1. Решая задачу одномерной оптимизации, найдем минимум этой функции по координате X1 при фиксированных остальных координатах - X11. В этом состоит первый шаг процесса оптимизации, заключающийся в спуске по координате X1.
Зафиксируем теперь все координаты, кроме X2. Снова решая одномерную задачу оптимизации, находим минимум функции по координате X2. Далее процедура повторяется до Xn. На этом заканчивается первая итерация.
Таким образом, метод покоординатного спуска сводит многомерную задачу оптимизации к многократному решению одномерных задач по каждой независимой пременной.
После каждой итерации вычисляется
D = Х1i+1 - X1i + Х2i+1 - X2i + .... +Хni+1 - Xni
и если D<=E , то вычисления прекращаются и последний набор Х-ов считается решением. В противном случае проводится следующая итерация.
Пример 5.1.
Число независимых переменных равняется двум. Ограничения отсутствуют. Требуется найти минимум функции
u = (X2-X12)2 + (1-X1)2
из начальной точки ( 0,5;0,5) c точностью 0,0001. Проанализировав функцию, заметим, что она будет иметь минимум, равный нулю. Для чего и первое, и второе слагаемое тоже должны быть равны нулю. Откуда координаты точки минимума (1;1).
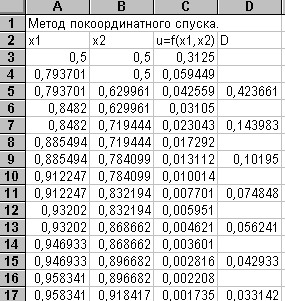
Решим эту задачу на EXCEL. Откроем новый рабочий лист. Выделим столбец А под значения X1, столбец В - под значения X2, в столбец С будем заносить значения целевой функции и, наконец, в столбец D - значения погрешности D.
Занесем в ячейки А3 и В3 значения начальных приближений, равных 0,5 и в ячейку С3 формулу =(В3-А3^2)^2+(1-A3)^2. Скопируем эту формулу в блок ячеек С4:С17. На этом заканчивается подготовительный этап.
1 итерация.
1 шаг. Скопируем содержимое ячейки В3 в ячейку В4. Сделаем текущей ячейку С4. Процесс одномерной оптимизации для нахождения X1 выполним с помощью подпрограммы EXCEL Поиск решения. Вызовем эту подпрограмму командой меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С4, а в поле Изменяя ячейки - адрес А4. Щелкнем по кнопке Выполнить и, во вновь открывшемся диалоге Результаты поиска решения щелкнем по кнопке ОК. В результате в ячейке А4 получим числовое значение, при котором целевая функция достигает минимального значения в ячейке С4 по координате X1.
2 шаг. Скопируем содержимое ячейки А4 в ячейку А5. Сделаем текущей ячейку С5. Дадим команду меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С5, а в поле Изменяя ячейки - адрес В5. Щелкнем по кнопке Выполнить и, во вновь открывшемся диалоге Результаты поиска решения щелкнем по кнопке ОК. В результате в ячейке В5 получим числовое значение, при котором целевая функция достигает минимального значения в ячейке С5 по координате X2.
3 шаг. Занесем в ячейку D5 формулу =ABS(A3-A5)+ABS(B3-B5) для вычисления погрешности решения на первом шаге. На этом заканчивается первая итерация.
Вторая и все последующие итерации проводятся аналогично, но с учетом соответствующих адресов ячеек. Например, во второй итерации будут участвовать адреса ячеек в 6 и 7 строках. Результаты проведения первых семи итераций представлены в таблице. Как видно, значения целевой функции уменьшаются от шага к шагу, но метод сходится чрезвычайно медленно.
Можно построить диаграмму изменения на каждой итерации, выделив блок А2:В17 с помощью Мастера Диаграмм, выбрав тип диаграммы XY-точечная и формат 2. На диаграмме хорошо видны перпендикулярные ломаные линии движения от точки к точке параллельно одной из осей координат.
