8.2. Метод Рунге-Кутта четвертого порядка.

По этому одношаговому методу вычисления проводятся по формуле

Y_i+1 = Y_i +hФ(X_i,Y_i), где

Ф(X_i,Y_i) = (K₁+2K₂+2K₃+K₄)/6

и К₁ = f(X_i,Y_i),

K₂=f(X_i+h/2,Y_i+hК₁/2),

K₃=f(X_i+h/2,Y_i+hК₂/2),

K₄=f(X_i+h,Y_i+hК₃).

Метод Рунге-Кутта имеет порядок точности h⁴ на всем отрезке интегрирования. Оценка погрешности метода очень затруднительна. Для оценки погрешности применяется правило двойного пересчета: расчет повторяют с шагом h/2 и погрешность более точного значения Yi* при шаге h/2 оценивают так

max {Y_i * - Y_iдля i=1,2,...,n .

Пример 8.2.

Решим задачу примера 8.1 методом Рунге-Кутта на том же рабочем листе. Отведем блок ячеек А17:А22 под значения Х с шагом 0,1. Соответственно, в столбце В будем вычислять Y , в столбцах С,D,E,F - значения коэффициентов К₁, K₂, K₃ и K₄. Столбец G отведем под Ф(X_i,Y_i). Основные формулы в строках 17 и 18 приведены в таблице.

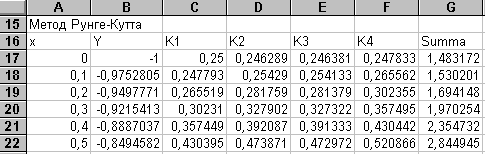
ячейка	формула
С17	=0,25*B17^2+A17^2
D17	=0,25*(B17+0,05*C17)^2+(A17+0,05)^2
E17	=0,25*(B17+0,05*D17)^2+(A17+0,05)^2
F17	=0,25*(B17+0,1*E17)^2+(A17+0,1)^2
G17	=C17+2*D17+2*E17+F17
B18	=B17+0,1*G17/6

Содержимое остальных ячеек в строках с 18 по 22 получается копированием из строк 17 и 18.Результаты решения приведены ниже. Для оценки погрешности следует провести те же вычисления с шагом, равным 0,05.

8.3. Метод прогноза и коррекции: метод Адамса.

В методах прогноза и коррекции каждое новое значение Yi определяют в два этапа. На первом определяют приближенное значение, которое называют прогнозом. Затем на втором этапе его уточняют с помощью итерационного процесса коррекции. Этот итерационный процесс продолжают до тех пор, пока не будет достигнута заданная точность решения. Таким образом, одно из достоинств метода прогноза и коррекции состоит в том, что одновременно с решением контролируется оценка погрешности.

С другой стороны, этот метод не является одношаговым, т.е. для вычисления прогноза необходимо иметь уже несколько вычисленных точек решения.

Пусть для уравнения

dY/dX = Y’ = f(X,Y),

с начальным условием Y(X₀) = Y₀ найдены каким-либо способом (методом Эйлера, Рунге-Кутта и т.п.) три последовательных значения искомой функции, так называемый начальный отрезок: Y₁, Y₂ и Y₃ для точек Х₁,Х₂ и Х₃, вычисленных с шагом h. Имея эти значения можно вычислить значения функции f₁=f(Х₁,Y₁),f₂₌f(Х₂,Y₂), f₃₌f(Х₃,Y₃) и f₀ =f(X₀,Y₀).

Метод Адамса состоит в вычислении Y₄ сначала по формуле прогноза

Y_4pred = Y₃+hФ_pred/24 = Y₃+h(55f₃-59f₂+37f₁-9f₀)/24

а затем уточнения этого значения, вычислив f_4pred=f(Х₄,Y_4pred) и применив формулу коррекции

Y_4kor= Y₃+hФ_kor/24 =Y₃+h(9f_4pred+19f₃-5f₂+ f₁)/24.

Эти формулы имеют достаточно большую точность и дают погрешность порядка h⁴. Обычно вычисляют D=Y_4kor - Y_4pred и если D<E, то переходят к вычислению следующей точки по тем же самым формулам, вводя переобозначения. Если же D>E, то проводят одну или несколько итераций по формуле коррекции, вычисляя f_4pred=f(Х₄,Y_4pred) и подставляя в эту формулу Y_4kor вместо Y_4pred. Как правило, для достижения заданной точности хватает одной или двух итераций.

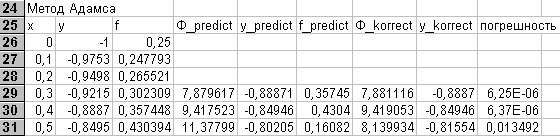
Пример 8.3.

Решим методом Адамса задачу примера 8.1. Из примера 8.2 возьмем вычисленные значения Y₁, Y₂ и Y₃. Продолжим вычисления по формулам Адамса для Х₄ и Х₅ на том же рабочем листе. Отведем блок А26:А31 под значения Х с шагом 0,1. В блок В26:В29 занесем значения Y из примера 9.2. В столбце С будем вычислять значения функции f на каждом шаге. В остальных столбцах будем последовательно располагать значения Ф_pred, Y_4pred, f_4pred, Ф_kor, Y_4kor, D. Необходимые для вычислений формулы приведены в таблице

ячейка	формула
C26	=0,25*B26^2+A26^2
D29	=55*C29-59*C28+37*C27-9*C26
E29	=B29+0,1/24*D29
F29	=0,25*E29^2+A30^2
G29	=9*F29+19*C29-5*C28+C27
H29	=B29+0,1/24*G29
I29	=ABS(E29-H29)
B30	=H29

Формулы в остальных ячейках, участвующих в вычислениях, получаются копированием. Результаты вычислений приведены в таблице

Видно, что погрешность удовлетворяет заданному значению для последних двух точек и итераций не требуется. В противном случае следовало бы воспользоваться встроенной подпрограммой EXCEL Поиск решения так, как это описано в разделе 6.