5.5. Условная оптимизация: подпрограмма excel “Поиск решения”.

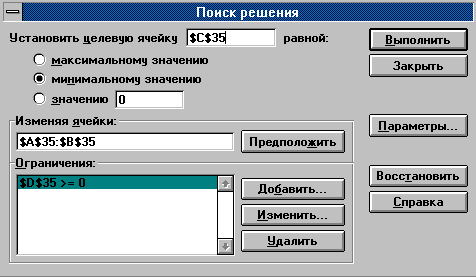
Подпрограмма Поиск решения имеет модификацию методов сопряженных градиентов и Ньютона для решения задач условной оптимизации. Следует отметить, что эта модификация работает успешно лишь для некоторых видов целевой функции - линейной и квадратичной и лишь для некоторых видов ограничений, например, типа шара, координатного параллелепипеда, гиперплоскости или полиэдра. После вызова подпрограммы командой меню Сервис- Поиск решения появляется диалог, в котором кроме уже знакомых Вам полей Установить целевую ячейку и Изменяя ячейки, следует обратить внимание на поле Ограничения и кнопки управления ограничениями Добавить, Изменить и Удалить. Например, чтобы задать новое ограничение следует щелкнуть по кнопке Добавить. В открывшемся новом диалоге Добавить ограничение нужно внести адрес одной или блока ячеек в поле Ссылка на ячейку, а затем указать тип ограничения и его условия. После этого нужно щелкнуть по кнопке ОК. Работа с другими кнопками управления не вызывает затруднений.

Выбор параметров подпрограммы вызывается щелчком по кнопке Параметры. Работа с открывшемся диалогом описана в п.5.3.

Продемонстрируем работу подпрограммы решением задачи примера 5.4.

Выделим ячейку А35 под переменную Х₁, ячейку В35 - под Х₂, в ячейку С35 запишем формулу целевой функции в обозначениях EXCEL

=(B35-A35^2)^2+(1- A35)^2, в ячейку D35 запишем формулу ограничений

=0,68 - (A35^2+B35^2). Сделаем ячейку С35 текущей и дадим команду меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С35, в поле Изменяя ячейки - адрес блока А35:В35. Теперь щелкнем по кнопке Добавить и в открывшемся новом диалоге в поле Ссылка на ячейку занесем адрес D35, выберем вид ограничения >= и правую часть ограничения - 0 (ноль). Щелкнув по кнопке ОК, вернемся к первоначальному диалогу.

Далее щелкнем по кнопке Параметры и выберем следующие переключатели: оценка - квадратичная, производные - прямые, метод - сопряженных градиентов. Щелкнув по кнопке Выполнить получим новый диалог Результаты поиска решения, в котором щелкнем по кнопке ОК. Результаты расчетов представлены в таблице. Особый интерес вызывает числовое значение в ячейке D35. Оно очень близко к нулю, но все же отрицательно, т.е. независимые переменные находятся в запрещенной области.

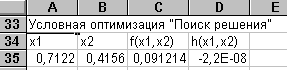
5.6. Условная оптимизация: линейное программирование.

В общем случае задача линейного программирования формулируется следующим образом: найти величины X₁, …, X_n, при которых достигается экстремум (максимум или минимум) линейной целевой функции

u = a₁X₁ + a₂X₂ + … + a_nX_n

и удовлетворяется система ограничений вида

c_i1X₁+ … + c_in X_n <= b_i,

c_k1X₁+ … + c_kn X_n = b_k,

c_p1X₁+ … + c_pn X_n >= b_p, где i # k # p.

На практике часто встречаются условия неотрицательности всех или части переменных

X_j >= 0, j = 1,2,…, s,

которые выделяют в особую группу.

Для решения задачи линейного программирования разработан специальный метод, названный симплекс – методом. Этот метод реализован в EXCEL в подпрограмме Поиск решения. В случае правильного решения задачи EXCEL печатает сообщение “Решение найдено. Все ограничения и условия оптимальности выполнены”. Если коэффициенты системы ограничений таковы, что эта система несовместна, то появится сообщение “Поиск не может найти подходящего решения”. Если же система ограничений такова, что область допустимых решений не ограничена сверху при поиске максимума ( или снизу при поиске минимума), то будет напечатано “Значения целевой ячейки не сходятся”.

Задача линейного программирования является достаточно распространенной задачей условной оптимизации, особенно в экономике. Решение этой задачи рассмотрим на примере задачи распределения ресурсов.

Пример 5.4.

Пусть некоторое предприятие может изготавливать изделия 4 типов. Для изготовления изделий требуются ресурсы 3 видов: трудовые ресурсы, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска одной единицы изделия каждого типа, называется нормой расхода. Пусть все нормы расхода известны и приведены в таблице

ресурсы	изделие1	изделие2	изделие3	изделие4
трудовые	1	1	1	1
сырье	6	6	4	3
финансы	4	5	10	13

Пусть известна также прибыль, получаемая от реализации каждого типа изделия

	изделие1	изделие2	изделие3	изделие4
прибыль	60	70	120	130

и располагаемое количество ресурсов

ресурсы	наличие
трудовые	16
сырье	110
финансы	100

Необходимо найти такие количества изделий каждого типа, чтобы прибыль предприятия была максимальной.

Введем некоторые обозначения.

Пусть

а_j - прибыль, получаемая от реализации единицы изделия j-го типа,

b_i - располагаемое количество i-го ресурса,

с_ij - норма расхода i-го ресурса для изготовления единицы j-го изделия,

xj - неизвестное количество изделий j-го типа.

Целевую функцию - суммарную величину прибыли предприятия - можно записать так

u = а₁x₁+а₂x₂+а₃x₃+а₄x₄  max.

Зная нормы расхода и располагаемое количество каждого ресурса, можно составить систему ограничений:

c₁₁x₁+c₁₂x₂+c₁₃x₃+c₁₄x₄ <= b₁

c₂₁x₁+c₂₂x₂+c₂₃x₃+c₂₄x₄ <= b₂

c₃₁x₁+c₃₂x₂+c₃₃x₃+c₃₄x₄<= b₃

Следует добавить также граничные условия из содержания задачи

x₁>=0, x₂>=0, x₃>=0, x₄>=0.

Для нашего примера

критерий оптимизации (целевая функция):

u = 60 x₁+70 x₂+120 x₃+130 x₄  max

ограничения

x₁+ x₂+ x₃+ x₄<=16

6 x₁+5 x₂+4 x₃+3 x₄<=110

4 x₁+6 x₂+10 x₃+13 x₄<=100

граничные условия

x₁>=0, x₂>=0, x₃>=0, x₄>=0.

Откроем новый рабочий лист и подготовим его к решению задачи. Внесем исходные данные так, как это показано на рисунке.

Теперь надо подготовить таблицы, связанные с решением задачи, ячейки для целевой функции и ограничений

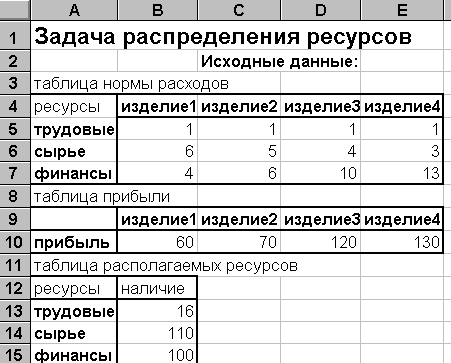
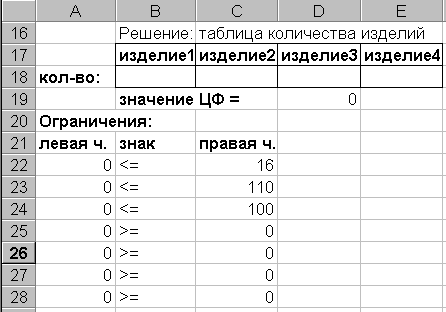
Далее внесем необходимые формулы для расчета:

ячейка	формула
D19	=CУММПРОИЗВ(В18:Е18;В10:Е10)
A22	=CУММПРОИЗВ(В18:Е18;В5:Е5)
A23	=CУММПРОИЗВ(В18:Е18;В6:Е6)
A24	=CУММПРОИЗВ(В18:Е18;В7:Е7)
A25	=B18
A26	=C18
A27	=D18
A28	=E18

После этого вызовем подпрограмму Сервис - Поиск решения. В появившемся диалоге внесем в окно Установить целевую ячейку адрес D19, в окно Изменяя ячейки адреса блока В18:Е18. Если в окне Ограничения оставлены какие-либо формулы от решения предыдущей задачи, их следует удалить по одному, выделяя каждое мышью и нажимая мышью кнопку Удалить. Затем следует внести нужные нам ограничения по одному, нажимая мышью кнопку Добавить. Каждый раз будет появляться новое диалоговое окно. Для первого ограничения в окно Ссылка на ячейку следует внести адрес А22, знак ограничения выбрать мышью из ниспадающего списка, а в правое окно занести адрес С22. Затем щелкнуть по кнопке Добавить и продолжить внесение ограничений.. Закончив ввод ограничений, щелкнем по кнопке ОК и снова попадем в окно Поиск решения.

Теперь щелкнем по кнопке Параметры. В открывшемся диалоге надо включить параметр Линейная модель. Щелкнув по кнопке ОК, возвратимся в окно Поиск решения.

Проверим, что переключатель указывает на поиск максимального значения и щелкнем по кнопке Выполнить. Появится новое диалоговое окно Результаты поиска решения. Если все формулы и ограничения были внесены правильно, то в этом окне будет написано “Решение найдено, Все ограничения и условия оптимальности выполнены”. Щелкнем по кнопке ОК и перейдем к анализу решения. Если же появится надпись “Поиск не может найти подходящего решения”, то щелкнем по кнопке Отмена и проверим правильность внесения исходных данных.

Результаты решения задачи нашего примера приведены в таблице

	изделие1	изделие2	изделие3	изделие4
кол-во	10	0	6	0

Значение целевой функции = 1320.

Анализ задачи линейного программирования на устойчивость и по пределам, который обычно проводят после получения решения, выходит за рамки данного пособия.