4.1. Метод дихотомии.

Для использования метода дихотомии должно быть дано:

а) формула целевой функции f(X),

б) численные значения а - левой границы и b - правой границы начального интервала неопределенности, на котором целевая функция унимодальна,

в) численное значение Е - точности нахождения значения Х, при котором f(X) принимает минимальное значение на [a,b].

Сущность метода состоит в том, что выбираются значения Х₁ и Х₂ так, чтобы они были как можно ближе к середине интервала неопределенности с=(a+b)/2. Обычно Х₁ = с-r и Х₂ = c+r, где r = E/3 или E/4 в зависимости от точности вычислений компьютера. Таким образом, на каждой итерации отбрасывается отрезок длиной (c-r), почти равной половине интервала неопределенности. Через К итераций начальный интервал неопределенности уменьшится до длины

d = (b-a)/2^K + r(2^K - 1)/2^(K-1) .

Итерации прекращаются, если d <= E.

Итак, алгоритм метода дихотомии состоит в следующем.

1) для заданных значений a и b вычисляются с=(a+b)/2, X₁ = c-E/3 и X₂=c+E/3,

2) вычисляются значения f(X₁) и f(X₂) и сравниваются между собой,

3) если f(X₁) > f(X₂), то а= X₁, иначе b= X₂,

4) если длина нового интервала d=(b-a) <=E, то вычисления останавливаются и в качестве решения можно взять любое значение Х, лежащее внутри этого интервала; в противном случае выполняется новая итерация.

Пример 4.1.

Пусть надо найти минимум функции f(X) = 2X² + e^-X. По правилам EXCEL эта функция должна быть записана так =2*Х^2 + EXP(-X), где вместо Х нужно подставить тот или иной адрес ячейки. Зададим Е= 0,0001.

Первый этап решения задачи состоит в нахождении начального интервала неопределенности, на котором функция f(X) унимодальна. С помощью EXCEL это легко сделать, протабулировав функцию f(X) в некоторых пределах, например, от -1 до 1 с шагом 0,2.

Откроем новый рабочий лист EXCEL. Поместим числовой ряд Х в блок А5:А16, оставив ячейку А4 пустой. В ячейку В4 занесем формулу =2*А4^2+EXP(-А4). Далее можно воспользоваться подпрограммой ТАБЛИЦА, вызвав ее командой меню Данные- Таблица и действуя так, как описано в примере 2.1. Как видно из таблицы, интервал неопределенности можно выбрать между а=0 и b=1.

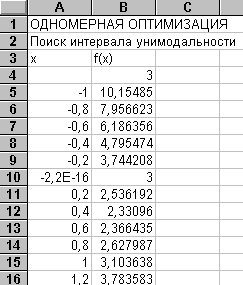
Запрограммируем решение нашей задачи методом дихотомии в блоке А24:G37, внеся необходимые числовые значения и формулы. Для изменения значений a и b используем функцию ЕСЛИ Мастера Функций. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 24 и 25. Формулы для остальных строк блока копируются из 25 строки.

Адрес	Формула
A24	0
B24	1
C24	=(A24+B24)/2-0,0001/3
D24	=(A24+B24)/2+0,0001/3
E24	=2*C24^2+EXP(-C24)
F24	=2*D24^2+EXP(-D24)
G24	=B24-A24
A25	=ЕСЛИ(E24>F24; C24; A24)
B25	=ЕСЛИ(E24<F24; D24; B24)
C25	=(A25+B25)/2-0,0001/3
D25	=(A25+B25)/2+0,0001/3
E25	=2*C25^2+EXP(-C25)
F25	=2*D25^2+EXP(-D25)
G25	=B25-A25

Из вычислений видно, что достаточно 12 итераций для получения решения с заданной точностью. Для построения диаграммы, иллюстрирующей изменения концов интервала неопределенности, следует выделить блок А23:В37 и воспользоваться Мастером Диаграмм, выбрав тип График и формат 1.